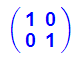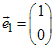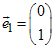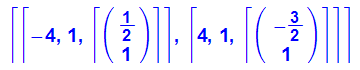Affine Abbildungen allgemein Einf. Bspl -6-
Eigenwerte, Eigenvektoren
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Jan 06 Update 05.01.06
Web: haftendorn.uni-lueneburg.de haftendorn.uni-lueneburg.de/ing-math
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben
######################################################
Dieses Notebook eignet sich für viele Beispiele.
"Grün" muss angepasst werden. (3-5 Stellen)
######################################################
Die Spalten der Abbildungsmatrix sind Bilder von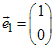

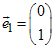
• Eh:=matrix([[1,0],[0,1]])

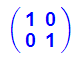
• A:=matrix([[2,-3],[-4,-2]])

• AE:=A-r*Eh

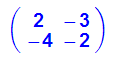
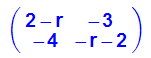
• charpoly:=linalg::det(AE)

• rlo:=solve(charpoly,r)

• linalg::eigenvalues(A)

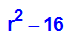
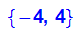
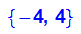
• ev:=linalg::eigenvectors(A)

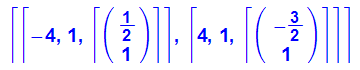
Vorn stehen die Eigenwerte mit ihrer Vielfachheit
Hinten die Eigenvektoren

• (ew[i]:=ev[i][1])$ i=1..2; 

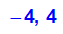
• (evec[i]:=ev[i][3][1])$i=1..2

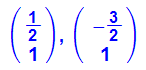
Dies sind die beiden Eigenvektoren

• A*evec[i] $ i=1..2

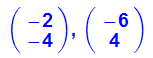
• (bildev[i]:=simplify(ew[i]*evec[i])) $ i=1..2 

#######################################################
+++++++++++++++++++++++++++++++++++++++++++++
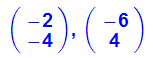
Definition eine Urbildes , hier eintragen

• myUr:=[[2,0],[2,1],[1,1],[1,3],[0,3],[0,0],[2,0],[1,1/2]]:
  myUrM:=linalg::transpose(matrix(myUr))

• npk:=nops(myUr):  //Anzahl der Punkte

++++++++++++++++++++++++++++++++++++++++++++++++
Verschiebung Translationsvektor hier eintragen
Weiterer Hilfsvektor a hier eintragen
Steigung m hier eintragen

• a:=0:
  m:=-1/2:
  trans:=matrix([0,0]):
  avec:=matrix([a,0]):

Aufblasen der Translationsvektoren zu Matrizen (als Funktion)

• tm:=tr->linalg::transpose(matrix([[tr[1],tr[2]] $ npk])):
  tm(trans):
  tm(avec)://soll hier der Drehpunkt sein.

##############################################
Zeichnen der Eigenvektoren

• (evecg[i]:=plot::Arrow2d([evec[i][1],evec[i][2]],LineColor=RGB::Orange))$ i=1..2:

• (bildevg[i]:=plot::Arrow2d([bildev[i][1],bildev[i][2]],LineColor=RGB::Brown))
                $ i=1..2;

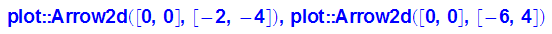
• polyg:=plot::Polygon2d([[0,0],[evec[1][1],evec[1][2]],
                [evec[1][1]+evec[2][1],evec[1][2]+evec[2][2]],
                [evec[2][1],evec[2][2]],[0,0]],Filled=TRUE,FillPattern=Solid);

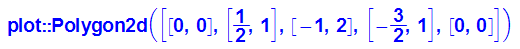
• bildpolyg:=plot::Polygon2d([[0,0],[bildev[1][1],bildev[1][2]],
                [bildev[1][1]+bildev[2][1],bildev[1][2]+bildev[2][2]],
                [bildev[2][1],bildev[2][2]],[0,0]],Filled=TRUE);

• plot(polyg,bildpolyg)

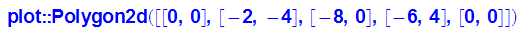
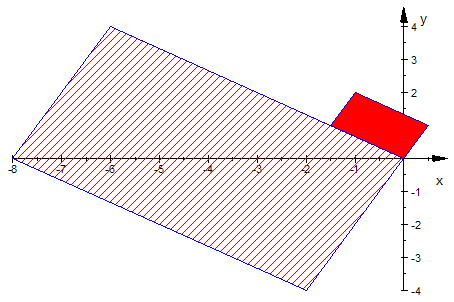
Dies ist das Parallelogramm der Eigenvektoren und sein Bild.

• urbild:=plot::Polygon2d(myUr, 
  LineWidth=1, LineColor=RGB::Green, Scaling=Constrained): 
  e1s:=plot::Arrow2d([A[1,1],A[2,1]]):
  e2s:=plot::Arrow2d([A[1,2],A[2,2]],LineColor=RGB::Black):
  avecg:=plot::Arrow2d([0,0],avec,LineColor=RGB::Magenta):
  plot(urbild,e1s,e2s,avecg,evecg[1],evecg[2],bildevg[1],bildevg[2],GridVisible=TRUE, 
  ViewingBox=[-5..7,-8..5]);

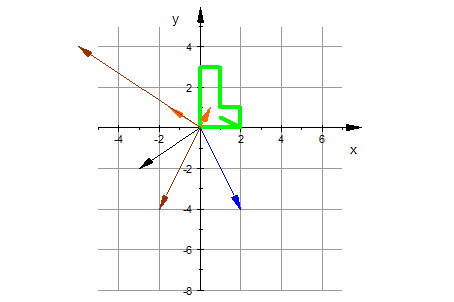
Transponieren, damit die Spalten die Urbild-Punkte sind:

• myUrM:=linalg::transpose(matrix(myUr)) ;

• myBM:=A*(myUrM-tm(avec)) +tm(avec)   //die Bildpunkte

• bildUr:=avec-A*avec;

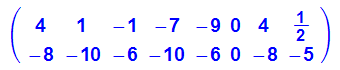
• myB:=[[myBM[1,j],myBM[2,j]] $ j=1..npk]:
  bildUrg:=plot::Arrow2d(avec,bildUr,LineColor=RGB::Brown):
  bild:=plot::Polygon2d(myB,LineWidth=1, LineColor=RGB::Red):
  plot(urbild,bild,e1s,e2s,avecg,bildUrg,evecg[1],evecg[2],
  bildevg[1],bildevg[2],polyg,bildpolyg,GridVisible=TRUE,
  ViewingBox=[-10..4,-10..5]):

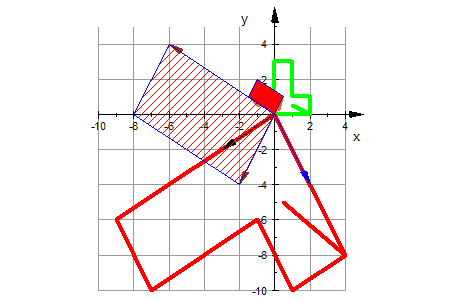
Das ist also eine allgemeine Affine Abbildung
ohne Translation nach allen Regeln der Kunst.
#######################################################