Affine Abbildungen 2d

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Jan 2011

0.1 Handling

0.2 Dieses ist das Einführungsbeispiel

0.3 Inhalt

Figure 1:

1 Urbild

1.1 Definition

Urbild

(%i18) myUr:transpose(matrix([2,0],[2,1],[1,1],[1,3],[0,3],[0,0],[2,0],[1,1/2]));

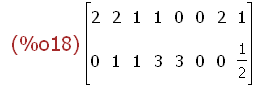
1.2 Zeichnen

(%i19) load(draw)$

(%i20) xmin:0$ xmax:7 $ ymin:0$ ymax:5$

(%i24) urbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],points_joined = true,color=green,
             line_width = 7, point_size = 1, point_type = up_triangle,
             grid=true,points(myUr) )$

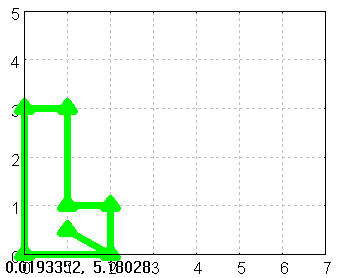
--> draw(urbild)$

Figure 2:

2 Abbildung

2.1 Abbildung der Einheitsvektoren

(%i1) A:transpose(matrix([3/2,1/2],[1/2,3/4]));

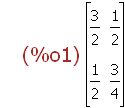
(%i25) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 7, point_size = 1, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=1, head_length=0.2,
             color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]))$

--> draw(startbild)$

Figure 3:

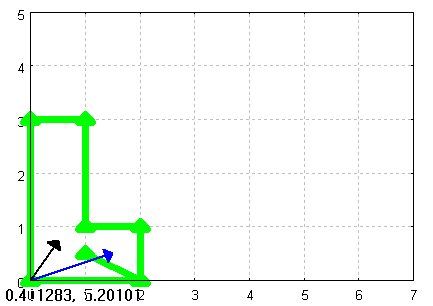
Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

2.2 Abbildungsgleichung für einen Punkt

Definition der Translation

(%i2) tx:3$ ty:2$

(%i4) tv:transpose(matrix([tx,ty]));

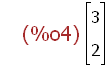
Allgemeine affine Abbildung

(%i7) f(xv):=A.xv+tv;

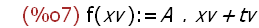
(%i8) f(xv);

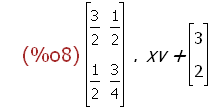
Abbildung eines beliebigen Punktes

(%i9) pv:transpose(matrix([px,py]));

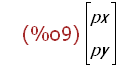
(%i10) f(pv);

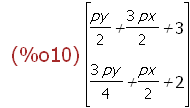
Abbildung eines konkreten Punktes

(%i11) pv:transpose(matrix([2,1]));

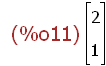
Nur affine Verzerrung

(%i26) A.pv;

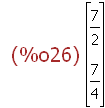
gesamt

(%i27) f(pv);
%,numer;

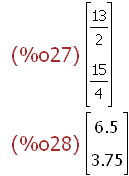
2.3 Affine Verzerrung für das ganze Urbild

(%i29) myUr;
myABild:A.myUr;
%,numer;

(%i32) ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 7, point_size = 1, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=1, head_length=0.2,
             color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]),
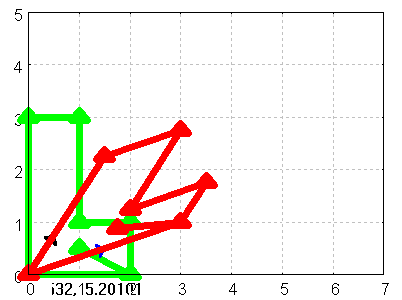
             line_width=7,point_size=1, color=red,
             points(myABild)
)$ draw(ABild)$

Figure 4:

2.4 Ganze affine Abbildung für das Urbild

Nun muss zu jedem dieser Bildpunkte der Translationsvektor
addiert werden. Dazu muss man ihn passend "aufblähen" zu einer
Transformationsmatrix.

(%i34) npk:length(transpose(myUr));

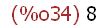
(%i35) mtv(tv):=block ([m],
                 m:tv,for i:1 thru npk-1 do ( m:addcol(m,tv)),return( m))$

(%i36) mtv(tv);

Gesamte Abbildung des Urbildes

(%i37) fm(myUr):=A.myUr+mtv(tv);

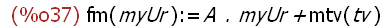
(%i38) myBild:fm(myUr);
%,numer;

(%i40) Bild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 7, point_size = 1, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=1, head_length=0.2,
             color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]),
             line_width=2,point_size=1, color=pink,
             points(myABild) ,
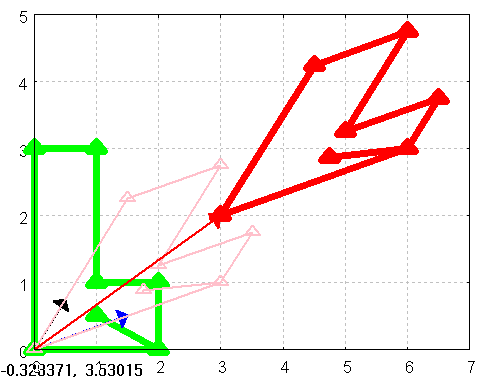
              color=red,vector([0,0],[tv[1,1],tv[2,1]]),
             line_width=7,color=red,
             points(myBild)
)$ draw(Bild)$

Figure 5:

3 Eigenwerte und Eigenvektoren

3.1 Vorgefertigte Beschaffung

(%i42) eigenvalues(A);

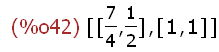
(%i43) ev_all:eigenvectors(A);

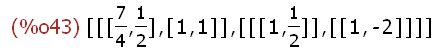
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte, dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

3.2 Beschaffung von Hand

(%i44) A;

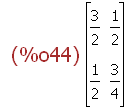
(%i45) E: matrix( [1,0], [0,1]);

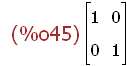
(%i46) A-x*E;

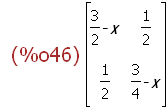
(%i47) determinant(A-x*E);

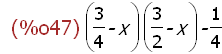
Auch dieses geht direkt

--> charpoly(A,x);

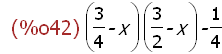
(%i48) solve(charpoly(A,x)=0,x);

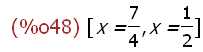
Hier sieht man die beiden Eigenwerte.

3.3 Darstellung, geometrische Bedeutung

(%i49) ew:ev_all[1][1]; ev1:ev_all[2][1][1];ev2:ev_all[2][2][1];

(%i54) evBild:gr2d(xrange = [-1,7], yrange = [-2,5],
             points_joined = true,color=green, line_width=2,
             points(myUr),
             grid=true, line_width=2,point_size=1, head_length=0.1,
             line_type=dots, color=orange,
             vector([0,0],[ev1[1],ev1[2]]),
             color=red,vector([0,0],[ev2[1],ev2[2]]),head_length=0.2,
             color=orange,
             vector([0,0],ew[1]*[ev1[1],ev1[2]]),
             color=red,vector([0,0],ew[2]*[ev2[1],ev2[2]]),
             line_width=2,point_size=1, color=red,
             points(myABild)
             )$ draw(evBild)$

Figure 6:

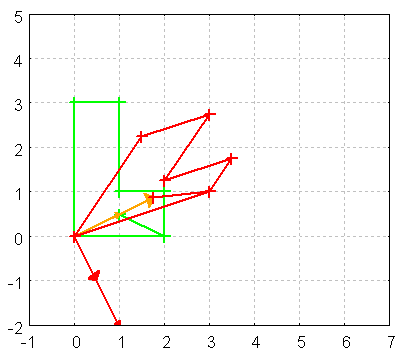
Die großen Pfeilspitzen bezeichnen die Bilder der
Eigenvektoren.

Bei dem Einführungsbeispiel sieht man, dass der eine Eigenwert
seinen Eigenvektor (orange) knapp verdoppelt *7/4, der andere
halbiert ihn (1/2).

4 Wirkung einer Linearen Abbildung

4.1 Urbild des Einheitskreises?

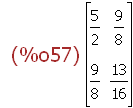
(%i56) A;

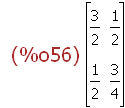
(%i57) S:A.A;

(%i61) pt:matrix([x,y]); p:transpose(pt);ellipseS:facsum(pt.S.p=1);

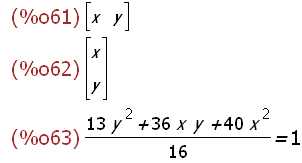
(%i91) draw(gr2d(line_width=3, color=red,grid=true,
             implicit(ellipseS, x, -1.5,1.5, y, -2,2),color=blue,
             implicit(x^2+y^2=1, x, -1.5,1.5, y, -2,2),

 grid=true, line_width=2,point_size=1, head_length=0.1,
             line_type=dots, color=orange,
             vector([0,0],[ev1[1],ev1[2]]/sqrt(5/4)),
             color=red,vector([0,0],[ev2[1],ev2[2]]/sqrt(5)),head_length=0.2,
             color=orange,
             vector([0,0],ew[1]^-1*[ev1[1],ev1[2]]/sqrt(5/4)),
             color=red,vector([0,0],ew[2]^-1*[ev2[1],ev2[2]]/sqrt(5))
            
            ))$

Figure 7:

--> charpoly(S,x);

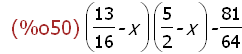
--> evs:eigenvectors(S);

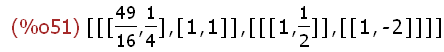
Dies passt zur Thoerie bei symmetrischem A: Eigenwerte quadriert,
dieselben Eigenvektoren

4.2 Transformationsmatrix

--> evs[2][1][1];

--> Tt:matrix(evs[2][1][1]/sqrt(5/4),evs[2][2][1]/sqrt(5));T:transpose(Tt)$

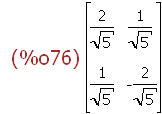
--> facsum(T.S.Tt);

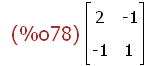
Diesen Schritt braucht man nicht wirklich zu machen, denn die Theorie
garantiert hier eine Diagonalmatrix mit den Eigenwerten in der
Hauptdiagonalen.

--> elliS:(49/16*x^2+1/4*y^2=1);

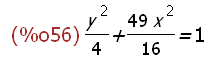
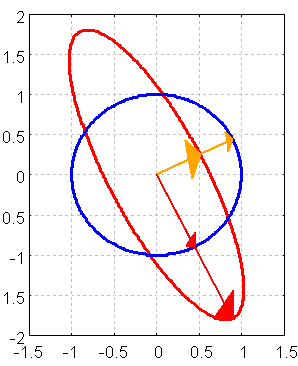
4.3 Bild des Einheitskreises

Auf welche Punkte wird der Einheitskreis abgebildet?

(%i67) A^^-1;

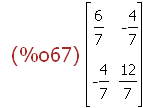
Die Inverse einer symmetrischen Matrix ist symmetrisch

(%i68) Q:A^^-2;

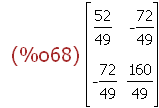
(%i72) ellipseQ:facsum(pt.Q.p=1);

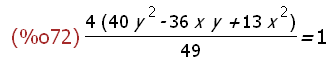
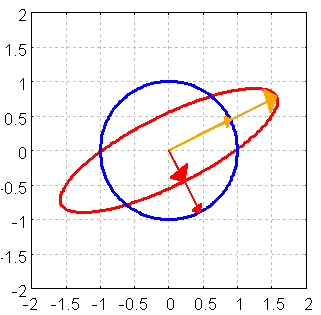
(%i90) draw(gr2d(line_width=3, color=red,grid=true,
             implicit(ellipseQ, x, -2,2, y, -2,2),color=blue,
             implicit(x^2+y^2=1, x, -1.5,1.5, y, -2,2),

 grid=true, line_width=2,point_size=1, head_length=0.1,
             line_type=dots, color=orange,
             vector([0,0],[ev1[1],ev1[2]]/sqrt(5/4)),
             color=red,vector([0,0],[ev2[1],ev2[2]]/sqrt(5)),head_length=0.2,
             color=orange,
             vector([0,0],ew[1]*[ev1[1],ev1[2]]/sqrt(5/4)),
             color=red,vector([0,0],ew[2]*[ev2[1],ev2[2]]/sqrt(5))
            
            ))$

Figure 8:

(%i92) charpoly(Q,x);

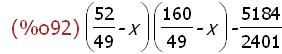
(%i93) evs:eigenvectors(Q);

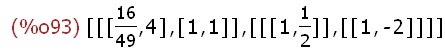
Dies passt zur Thoerie bei symmetrischem A: Kehrwerte der
Eigenwerte quadriert,dieselben Eigenvektoren