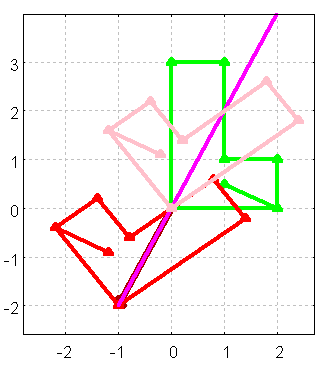
Affine Abbildungen 2d in Schule

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Jan 2011

0.1 Handling

0.2 Schulabbildungen, kompakt

0.3 Inhalt

1 Def. Urbild
2 Drehung um (0,0) um alpha
    2.1 alpha beliebig
    2.2 Punktspiegelung
3 Spiegelungen
    3.1 an x-Achse
    3.2 an y-Achse
4 Spiegelung an bel. Ursprungsgeraden
5 Streckungen
    5.1 Zentrische- und Hauptachsen-Streckungen
    5.2 Achsenstreckungen längs y=m*x
6 Verschiebung
7 Gleitspiegelung

1 Urbild

1.1 Definition

1.2 Zeichnen

2 Drehung um alpha

2.1 Definition der Drehung

Bilder des ersten und zweiten Einheitsvektors eintragen

(%i32) alpha:%pi/6;

(%i121) D(alpha):=matrix([cos(alpha),-sin(alpha)],[sin(alpha),cos(alpha)]);

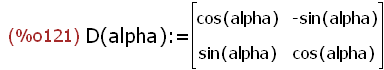
(%i34) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5 ,head_length=0.1,
             color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]))$
draw(startbild)$

Figure 2:

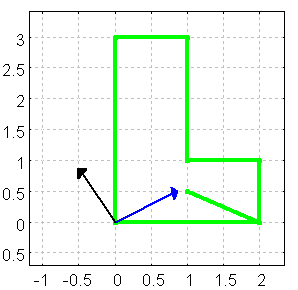
Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

2.2 Affine Verzerrung für das ganze Urbild

(%i122) myUr;
fpprintprec:4;
myABild:D(alpha).myUr;
%,numer;

--> ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild)
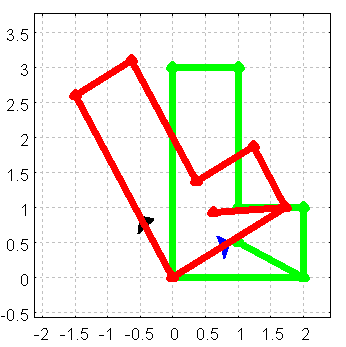
)$ draw(ABild)$

Figure 3:

2.3 Eigenwerte und Eigenvektoren

(%i127) ev_all: eigenvectors(D(%pi));

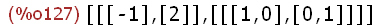
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i128) charpoly(D(%pi),x);

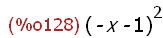
(%i129) solve(charpoly(D(%pi),x)=0,x);

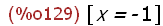
Hier sieht man den doppelten Eigenwert.

3 Spiegelung

3.1 Spiegelung an x-Achse

3.2 Abbildung der Einheitsvektoren

Bilder des ersten und zweiten Einheitsvektors eintragen

(%i130) Spx:matrix([1,0],[0,-1]);

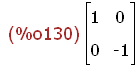
(%i131) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5 ,head_length=0.1,
             color=blue,vector([0,0],[Spx[1,1],Spx[2,1]]),
             color=black,vector([0,0],[Spx[1,2],Spx[2,2]]))$
draw(startbild)$

Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

(%i93) pv:transpose(matrix([px,py]));

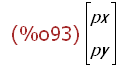
3.3 Affine Verzerrung für das ganze Urbild

(%i133) myUr;
fpprintprec:4;
myABild:Spx.myUr;
%,numer;

--> ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Spx[1,1],Spx[2,1]]),
             color=black,vector([0,0],[Spx[1,2],Spx[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild)
)$ draw(ABild)$

Figure 4:

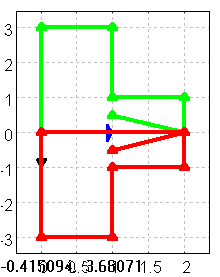
3.4 Eigenwerte und Eigenvektoren

(%i137) ev_all: eigenvectors(Spx);

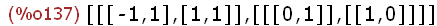
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i138) charpoly(Spx,x);

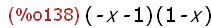
(%i139) solve(charpoly(Spx,x)=0,x);

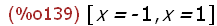
Hier sieht man die beiden Eigenwerte.

3.5 Spiegelung an y-Achse

3.6 Abbildung der Einheitsvektoren

Bilder des ersten und zweiten Einheitsvektors eintragen

(%i140) Spy:matrix([-1,0],[0,1]);

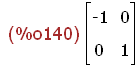
(%i141) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5 ,head_length=0.1,
             color=blue,vector([0,0],[Spy[1,1],Spy[2,1]]),
             color=black,vector([0,0],[Spy[1,2],Spy[2,2]]))$
draw(startbild)$

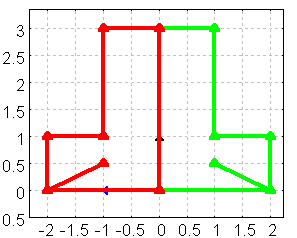
Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

--> pv:transpose(matrix([px,py]));

3.7 Affine Verzerrung für das ganze Urbild

(%i110) myUr;
fpprintprec:4;
myABild:Spy.myUr;
%,numer;

(%i114) ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Spy[1,1],Spy[2,1]]),
             color=black,vector([0,0],[Spy[1,2],Spy[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild)
)$ draw(ABild)$

Figure 5:

3.8 Eigenwerte und Eigenvektoren

(%i143) ev_all: eigenvectors(Spy);

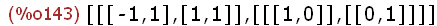
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i144) charpoly(Spy,x);

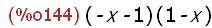
(%i145) solve(charpoly(Spy,x)=0,x);

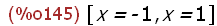
Hier sieht man die beiden Eigenwerte.

4 Spiegelung an Ursprungsgeraden y=a/b*x

4.1 Bestimmung des Drehwinkels

(%i120) gw:atan(m);

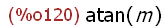
(%i166) kill(m);

(%i167) Sp(m):=D(atan(m)).Spx.D(-atan(m));Sp(m);

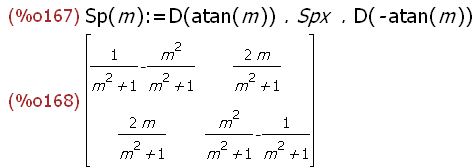
Bilder des ersten und zweiten Einheitsvektors können
abgelesen werden.

(%i169) Sp(2);

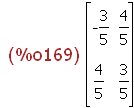
(%i194) Sp(-1/2);

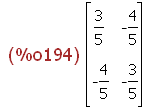
(%i172) m:2;

(%i173) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5 ,head_length=0.1,
             color=blue,vector([0,0],[Sp(m)[1,1],Sp(m)[2,1]]),
             color=black,vector([0,0],[Sp(m)[1,2],Sp(m)[2,2]]))$
draw(startbild)$

Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

--> pv:transpose(matrix([px,py]));

4.2 Affine Verzerrung für das ganze Urbild

(%i177) myUr;
fpprintprec:4;
myABild:Sp(m).myUr;
%,numer;

(%i187) ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Sp(m)[1,1],Sp(m)[2,1]]),
             color=black,vector([0,0],[Sp(m)[1,2],Sp(m)[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild), color="#ff00ff",
             polygon([-0.5,2],[-1,4])
)$ draw(ABild)$

Figure 6:

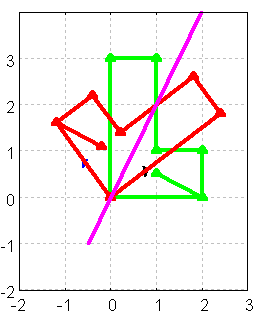
4.3 Eigenwerte und Eigenvektoren

(%i189) ev_all: eigenvectors( Sp(m));

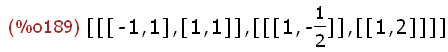
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i190) charpoly(Sp(m),x);

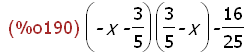
(%i191) solve(charpoly(Sp(m),x)=0,x);

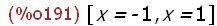
Hier sieht man die beiden Eigenwerte.

(%i193) determinant(Sp(m));

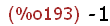
5 Steckungen

5.1 zentrische- und Hauptachsenstreckungen

Bilder des ersten und zweiten Einheitsvektors eintragen

(%i236) kill(k1,k2);

Zentrische Streckungen: k1=k2
Achsenstreckungen parallel zur y-Achse: k1=1
Achsenstreckungen parallel zur x-Achse: k2=1

(%i237) Str(k1,k2):=matrix([k1,0],[0,k2]);

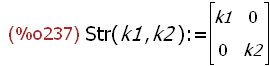
(%i240) k1:3/2$ k2:1/2$ Str(k1,k2);

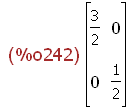
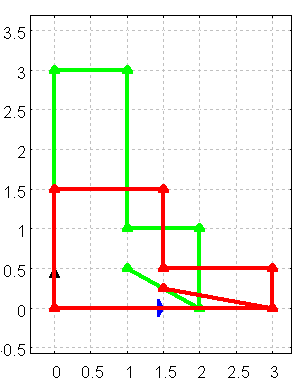
(%i221) startbild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5 ,head_length=0.1,
             color=blue,vector([0,0],[Str(k1,k2)[1,1],Str(k1,k2)[2,1]]),
             color=black,vector([0,0],[Str(k1,k2)[1,2],Str(k1,k2)[2,2]]))$
draw(startbild)$

Der blaue Vektor ist das Bild des x-Einheitsvektors.
Der schwarze Vektor ist das Bild des y-Einheitsvektors.

5.2 Streckung für das ganze Urbild

(%i225) myUr;
fpprintprec:4;
myABild:Str(k1,k2).myUr;
%,numer;

(%i268) ABild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Str(k1,k2)[1,1],Str(k1,k2)[2,1]]),
             color=black,vector([0,0],[Str(k1,k2)[1,2],Str(k1,k2)[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild)
)$ draw(ABild)$

Figure 7:

5.3 Eigenwerte und Eigenvektoren

(%i233) ev_all: eigenvectors(Str(k1,k2));

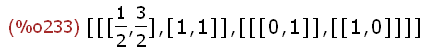
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i234) charpoly(Str(k1,k2),x);

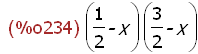
(%i235) solve(charpoly(Str(k1,k2),x)=0,x);

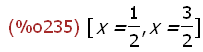
Hier sieht man den die Streckfaktoren als Eigenwerte.

5.4 Streckungen in Richtung der Geraden y=m*x

(%i297) kill(m,k,k1,k2);

(%i304) Strachs(m,k):=D(atan(m)).Str(k,1).D(-atan(m));

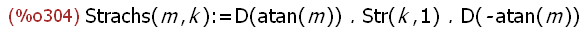
(%i305) Strachs(m,k);

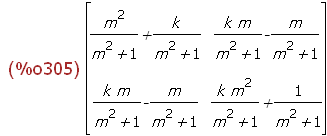
(%i306) m:2$ k:3/2;

5.5 Streckung für das ganze Urbild

(%i308) myUr;
fpprintprec:4;
myABild:Strachs(m,k).myUr;
%,numer;

(%i342) ZBild:gr2d(xrange = [-1,5], yrange = [-3,7],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Strachs(m,k)[1,1],Strachs(m,k)[2,1]]),
             color=black,vector([0,0],[Strachs(m,k)[1,2],Strachs(m,k)[2,2]]),
             line_width=4,point_size=0.5, color="#00aa00",
             points(D(-atan(m)).myUr) ,color="#ff00ff",
             polygon([-1,2],[-2,4]),color=pink,
             points(Str(k,1).D(-atan(m)).myUr))$

(%i343) draw(ZBild)$

Figure 8:

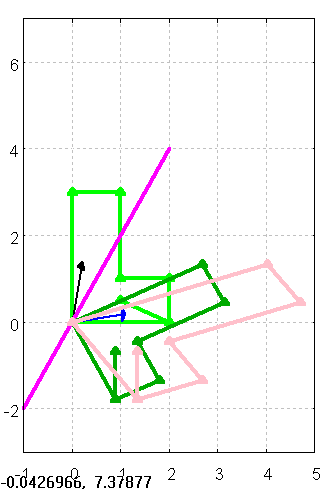
(%i356) ABild:gr2d(xrange = [-1,3], yrange = [-2,5],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             color=blue,vector([0,0],[Strachs(m,k)[1,1],Strachs(m,k)[2,1]]),
             color=black,vector([0,0],[Strachs(m,k)[1,2],Strachs(m,k)[2,2]]),
             line_width=4,point_size=0.5, color=red,
             points(myABild) ,color="#ff00ff",
             polygon([-1,2],[-2,4]), line_type=dots, line_width=1,
             polygon([2,-2],[-1,1])
)$ draw(ABild)$

Figure 9:

--> points(D(atan(m)).Str(k,1).D(-atan(m)).myUr)

(%i325) k;m;

5.6 Eigenwerte und Eigenvektoren

(%i358) ev_all: eigenvectors(Strachs(m,k));

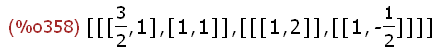
Die Liste ist so zu deuten:
Erste Unterliste: die beiden Eigenwerte,
dann ihre Vielfachheiten.
Zweite Unterliste: erster Eigenvektor, zweiter Eigenvektor

(%i359) charpoly(Strachs(m,k),x);

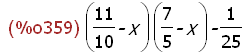
(%i360) solve(charpoly(Strachs(m,k),x)=0,x);

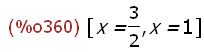
(%i361) kill(m,k);

(%i362) ev_all: eigenvectors(Strachs(m,k));

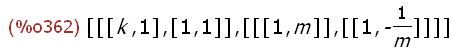
Hier sieht man den die Streckfaktoren als Eigenwerte.
Die Streckachse und die zu ihr senkrechten Richtungen
sind Eigenrichtungen.

(%i365) charpoly(Strachs(m,k),x);
expand(%);

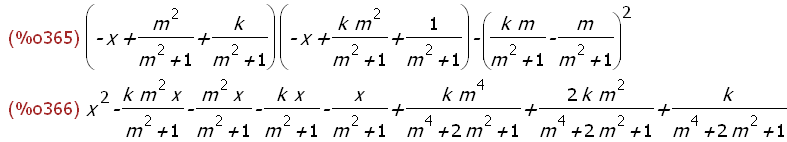
(%i364) solve(charpoly(Strachs(m,k),x)=0,x);

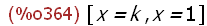
Hier sieht man den die Streckfaktoren als Eigenwerte.

6 Verschieben

6.1 Abbildungsgleichung für einen Punkt

Definition der Translation

(%i195) tx:-3$ ty:-2$

(%i197) tv:transpose(matrix([tx,ty]));

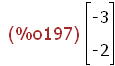
Eins-Abbildung Identität

(%i198) E:matrix([1,0],[0,1]);

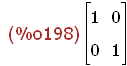
(%i199) f(xv):=E.xv+tv;

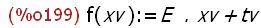
(%i200) f(xv);

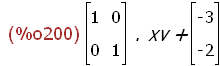
Abbildung eines beliebigen Punktes

(%i201) pv:transpose(matrix([px,py]));

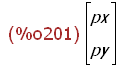
(%i202) f(pv);

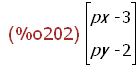
Nun muss zu jedem dieser Bildpunkte der Translationsvektor
addiert werden. Dazu muss man ihn passend "aufblähen" zu einer
Transformationsmatrix.

(%i203) npk:length(transpose(myUr));

(%i204) mtv(tv):=block ([m],
                 m:tv,for i:1 thru npk-1 do ( m:addcol(m,tv)),return( m))$

(%i205) mtv(tv);

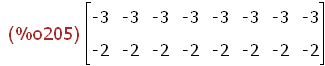
Gesamte Abbildung des Urbildes

(%i207) fm(myUr):=E.myUr+mtv(tv);

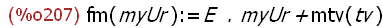
(%i208) myBild:fm(myUr);
%,numer;

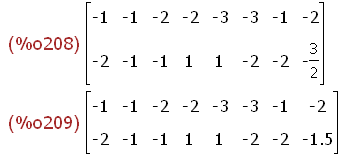
(%i212) Bild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             /*color=blue,vector([0,0],[A[1,1],A[2,1]]),
             color=black,vector([0,0],[A[1,2],A[2,2]]),*/
             line_width=2,point_size=0.5, color=pink,
             /*points(myABild) ,*/
              color=red,vector([0,0],[tv[1,1],tv[2,1]]),
             line_width=4,color=red,
             points(myBild)
)$ draw(Bild)$

Figure 10:

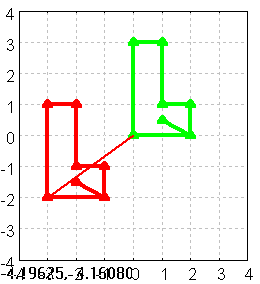
7 Gleitspiegelung

Definition der Translation

(%i243) tx:-1$ ty:-2$

(%i245) tv:transpose(matrix([tx,ty]));

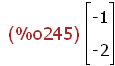
Eins-Abbildung Identität

(%i246) E:matrix([1,0],[0,1]);

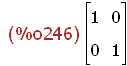
(%i247) f(xv):=E.xv+tv;

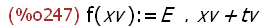
(%i248) f(xv);

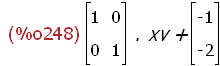
Abbildung eines beliebigen Punktes

--> pv:transpose(matrix([px,py]));

--> f(pv);

Nun muss zu jedem dieser Bildpunkte der Translationsvektor
addiert werden. Dazu muss man ihn passend "aufblähen" zu einer
Transformationsmatrix.

(%i249) npk:length(transpose(myUr));

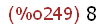
(%i250) mtv(tv):=block ([m],
                 m:tv,for i:1 thru npk-1 do ( m:addcol(m,tv)),return( m))$

(%i251) mtv(tv);

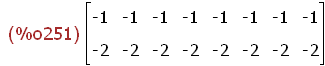
Gesamte Abbildung des Urbildes

(%i260) fm(myUr):=Sp(m).myUr+mtv(tv);

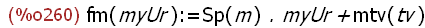
(%i261) m:2;

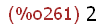
(%i262) myBild:fm(myUr);
%,numer;

(%i276) Bild:gr2d(xrange = [xmin,xmax], yrange = [ymin,ymax],
             points_joined = true,color=green,
             line_width = 4, point_size = 0.5, point_type = up_triangle,
             grid=true,points(myUr) ,
             grid=true, line_width=2,point_size=0.5, head_length=0.1,
             /*color=blue,vector([0,0],[Sp(m)[1,1],Sp(m)[2,1]]),
             color=black,vector([0,0],[Sp(m)[1,2],Sp(m)[2,2]]),*/
             line_width=7,point_size=0.5,
              color="#aa0000",vector([0,0],[tv[1,1],tv[2,1]]),
             line_width=4,color=red,line_width=4,
             points(myBild) ,color="#ff00ff",
             polygon([-1,2],[-2,4]),
             color=pink,points(Sp(m).myUr)
)$ draw(Bild)$

Figure 11: