A:= matrix([[3,1],[1,3]])
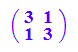
Diagonalisierung von Matrizen
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD4 , 23.06.07 Update 15.07.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Für symmetrische Matrizen sind reelle EW gesichert.
Für diese ist auch gesichert, dass die EV zu verschiedenen EW senkrecht aufeinander stehen.
Darum werden nur in vielen Anwendungen möglichst symmetrische Matizen betrachtet.
Es werden 4 Fälle betrachtet:
Fall 1 2d-Matrix, 2 versch. EW
Fall 2-4 3d-Matrizen
Fall 2 alle 3 EW verschieden
Fall3 einer doppelt 0, einer =/=0
Fall 4 einer 0, der andere doppelt
Das in den Dateien Konstruktion rückwärts für Kegelschnitte und Quadriken
vorgestellte Verfahren zum Aufstellen einer Matrix mit selbst gewählten EV und EW
ist eicht auf höhere Dimensionen übertragbar.
Es ist zum Erzeugen von weiteren Beispielen zu empfehlen.
-----------------------------
Fall 1: 2d-Matrix, 2 Eigenwerte, verschieden
A:= matrix([[3,1],[1,3]])
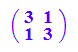
evli:=linalg::eigenvectors(A)
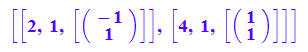
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
k1 :=evli[1][1]; k2 :=evli[2][1];
ev1:=evli[1][3][1]:
ev2:=evli[2][3][1]:
![]()
![]()
Prüfung, ob die Eigenvektoren senkrecht aufeinander stehen.
Ggf. Herstellung eine ONS aus Eigenvektoren.
linalg::scalarProduct(ev1,ev2)
![]()
Aufstellen der Transformationsmatrix P aus den Eigenvektoren.
P:=ev1.ev2

Pt:=linalg::transpose(P) //hier unnötig

Diagonalisierung
Pt*A*P

#########################################
Fall 2: 3d-Matrix, 3 verschiedene Eigenwerte
A:=matrix([[7,-2,-1],[-2,7,-1],[-1,-1,4]])
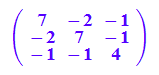
Liste aus Eigenwert, Vielfachheit und Eigenvektor
evli:=linalg::eigenvectors(A)
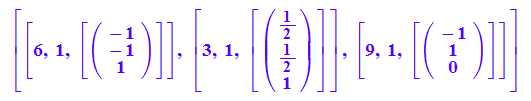
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
k1 :=evli[1][1]; k2 :=evli[2][1]; k3 :=evli[3][1];
ev1:=evli[1][3][1]:
ev2:=evli[2][3][1]:
ev3:=evli[3][3][1]:
![]()
![]()
![]()
linalg::scalarProduct(ev1,ev2),
linalg::scalarProduct(ev2,ev3),
linalg::scalarProduct(ev1,ev3);
![]()
Prüfung, ob die Eigenvektoren senkrecht aufeinander stehen.
(was für symm. Matrizen und verschiedene EW von selbst so ist.
Herstellung eine ONS aus Eigenvektoren.
ev1n:=linalg::normalize(ev1):
ev2n:=linalg::normalize(ev2):
ev3n:=linalg::normalize(ev3):
Aufstellen der Transformationsmatrix P aus den Eigenvektoren.
P:=ev1n.ev2n.ev3n
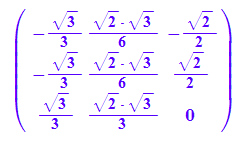
Pt:=linalg::transpose(P)
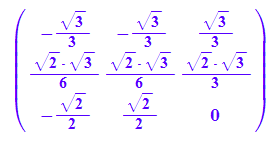
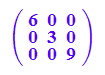
Diagonalisierung
Pt*A*P
####################################################
Fall 3: 3d-Matrix, 0 als doppelter Eigenwert,
einer verschieden von 0
A:=matrix([[1,1,1],[1,1,1],[1,1,1]])

Liste aus Eigenwert, Vielfachheit und Eigenvektor
evli:=linalg::eigenvectors(A)
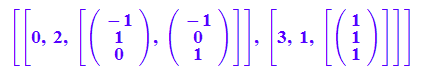
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
k1 :=evli[1][1]; k2 :=evli[2][1];
ev1:=evli[1][3][1]:
ev2:=evli[1][3][2]:
ev3:=evli[2][3][1]:
![]()
![]()
linalg::scalarProduct(ev1,ev2),
linalg::scalarProduct(ev2,ev3),
linalg::scalarProduct(ev1,ev3);
![]()
Prüfung, ob die Eigenvektoren senkrecht aufeinander stehen.
Das tun sie nicht. Zu einem doppelten EW gehört ein 2-dim-Eigenraum.
Aus diesem wird ein i.a. nicht orthogonales Paar angegeben.
Der dritte EV ist aber orthogonal zu diesem Eigenraum. Daher kann man
mit dem Kreuzprodukt einen passenden anderen auswählen.
---------------------
Herstellung eine ONS aus Eigenvektoren.
ev2:=linalg::crossProduct(ev1,ev3)
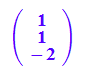
ev1n:=linalg::normalize(ev1):
ev2n:=-linalg::normalize(ev2): //negativ genommen, s.u.
ev3n:=linalg::normalize(ev3):
Aufstellen der Transformationsmatrix P aus den Eigenvektoren.
P:=ev1n.ev2n.ev3n;
Pt:=linalg::transpose(P)

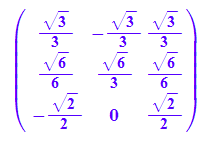
linalg::det(P)
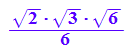
In vielen Anwendungen ist es vorteilhaft, wenn die Determinate von P positiv ist.
Das erreicht man, wenn die EV ein Rechtssystem bilden. Man kann sie vertauschen oder
auch einen mit -1 multiplizieren, um das zu erreichen.
Diagonalisierung
Pt*A*P
Fall 4: 3d-Matrix, 2 verschiedene Eigenwerte,
einer 0, ein positiver doppelt
A:=matrix([[2,1,-1],[1,2,1],[-1,1,2]])
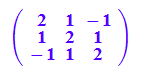
Liste aus Eigenwert, Vielfachheit und Eigenvektor
evli:=linalg::eigenvectors(A)

Herausgreifen der EigenWerte ki und der Eigenvektoren evi
k1 :=evli[1][1]; k2 :=evli[2][1]; k3 :=evli[2][1];
ev1:=evli[1][3][1]:
ev2:=evli[2][3][1]:
ev3:=evli[2][3][2]:
![]()
![]()
![]()
linalg::scalarProduct(ev1,ev2),
linalg::scalarProduct(ev2,ev3),
linalg::scalarProduct(ev1,ev3);
![]()
Prüfung, ob die Eigenvektoren senkrecht aufeinander stehen.
Das tun sie nicht. Zu einem doppelten EW gehört ein 2-dim-Eigenraum.
Aus diesem wird ein i.a. nicht orthogonales Paar angegeben.
Der dritte EV ist aber orthogonal zu diesem Eigenraum. Daher kann man
mit dem Kreuzprodukt einen passenden anderen auswählen.
Für höhere Dimensionen kann man mit dem Gram-Schmidtschen
Orthogonalisierungsverfahren eine ONS herstellen.
-----------------
Herstellung eine ONS aus Eigenvektoren.
ev2:=linalg::crossProduct(ev1,ev3)
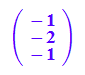
ev1n:=linalg::normalize(ev1):
ev2n:=-linalg::normalize(ev2): //Negativ genommen, s.u.
ev3n:=linalg::normalize(ev3):
Aufstellen der Transformationsmatrix P aus den Eigenvektoren.
P:=ev1n.ev2n.ev3n;
Pt:=linalg::transpose(P)

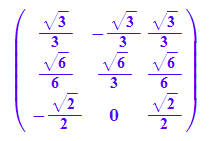
linalg::det(P)
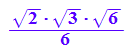
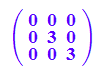
Diagonalisierung
Pt*A*P
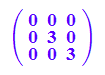
expand(Pt*A*P)
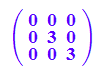
float(Pt*A*P)
