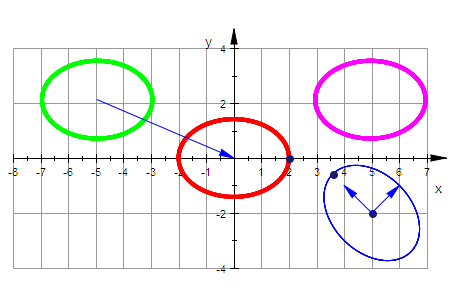
A:= matrix([[3,1],[1,3]]);
ewe:=linalg::eigenvalues(A)
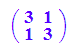
![]()
Ellipse in allgemeiner Lage
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4 Juni 07 Update 29.06.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Ganzzahlige Eigenwerte,
-----------------------------------
Zuerst Konstruktion eines guten Beispiels.
Dass die folgende Matrix zwei ganze positive Eigenwerte hat ist woanders schon gesichert.
A:= matrix([[3,1],[1,3]]);
ewe:=linalg::eigenvalues(A)
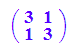
![]()
M:=[5,-2]: d1:=ewe[1]*ewe[2]:
keg:=A[1,1]*(x-M[1])^2+2*A[1,2]*(x-M[1])*(y-M[2])+A[2,2]*(y-M[2])^2-d1
![]()
##############################################
keg:=expand(keg)
![]()
kegp:=plot::Implicit2d(keg,x=-2..7,y=-4..2):
plot(kegp,Scaling=Constrained);
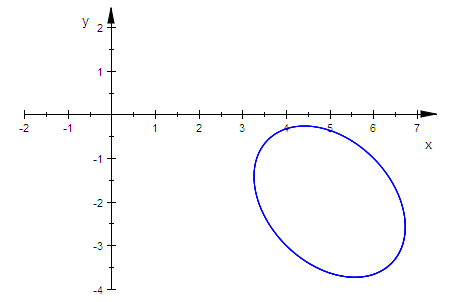
Dieser Kegelschnitt ist offenbar eine Ellipse.
Durchführung einer Hauptachsentransformation
Bestimmung der Achsenrichtungen:
evli:=linalg::eigenvectors(A)
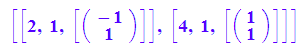
Eigenwerte mit ihrer Vielfachheit und ihrem Eigenvektor.
ev1:=evli[1][3][1];
ev2:=evli[2][3][1];
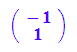
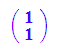
float(ev1),float(ev2)
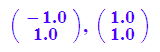
Einzeichnen der Eigenvektoren:
ev1p:=plot::Arrow2d(ev1):
ev2p:=plot::Arrow2d(ev2):
plot(kegp,ev1p,ev2p, Scaling=Constrained)
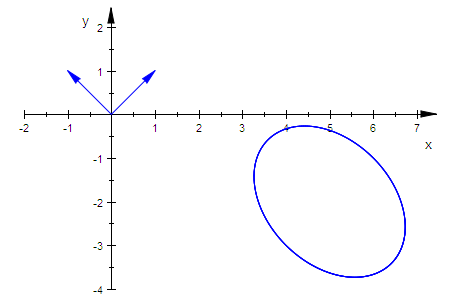
Wie erwartet sind die Eigenvektoren die Richtungen der Hauptachsen des Kegelschnittes.
---------------------------------------------------
Bestimmung der Kegelschnittgleichung ist ganz einfach, wenn man die Theorie gleich verwendet:
Man nimmt die Eigenwerte als Koeffizienten der quadratischen Glieder.
Die gemischten lässt man weg. Oben ist die ursprüngliche Konstante d1 als Produkt
der Eigenwerte gewählt. Dadurch kann man hier d1 verwenden.
Wie eventuelle lineare Glieder umgeformt werden, wird in anderen Beispielen gezeigt.
Wenn man d1 nicht weiß, ergibt es sich dann aus diesen Umformungen erst später.
ew1:=evli[1][1];
ew2:=evli[2][1];
![]()
![]()
kegH:=ew1*x^2+ew2*y^2-d1;
float(%)
![]()
![]()
Diesen in Hauptachsenlage transformierten Kegelschnitt zeichnen wir ein:
kegHp:=plot::Implicit2d(kegH=0,x=-2..7,y=-4..2,
LineWidth=1,LineColor=[1,0,0]):
plot(kegp, kegHp,ev1p,ev2p,Scaling=Constrained)
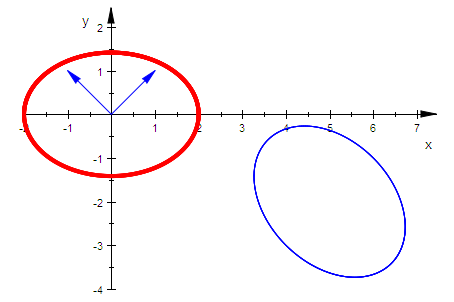
Soll die gegebene blaue Ellipse in rote in Hauptachsenlage abgebildet werden,
so kann das geschehen durch eine Drehung um den Ursprung, evt. verknüpft mit einer
Achsenspiegelung an einer der Koordinatenachsen, gefolgt von einer Verschiebung.
und
Aus den normierten Eigenvektoren erstellt man eine Matrix P.
Die Eigenvektoren stehen gleich von alleine senkrecht aufeinander, wenn die Eigenwerte verschieden sind.
P ist dann eine Orthonormal-Matrix. Für solche ist die inverse Matrix
gleich der transponierten Matrix, bezeichnet mit Pt (oder mit hochstelltem T).
Die Transformationsmatrix, die den Kegelschnitt in eine Lage bewegt, bei der die Hauptachsen parallel
zu den Koordinatenachsen sind, ist Pt.
Die Theorie sagt nun, dass Pt*A*P die Diagonalmatrix aus den Eigenwerten ist.
Davon kann man sich hier überzeugen:
ev1n:=linalg::normalize(ev1):
ev2n:=linalg::normalize(ev2):
P:=ev1n.ev2n
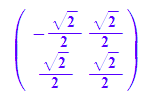
float(P)

Pt:=linalg::transpose(P)
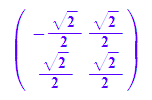
float(Pt)

Diagonalisierung, die klappt immer, wenn die EV eine ONB bilden,
wenn man also so ein P aufstellen kann.
Simplify(Pt*A*P);
float(Pt*A*P)
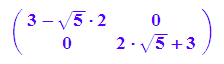
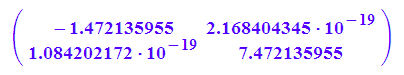
Die winzigen 10^-19 Werte sind numerisch 0.
---------------------------------------------------------------
Vektorschreibweise für die Abbildung und die
Quadrikgleichungen, die sich durch Einsetzen ergeben:
Abbildung der linearen Terme erfordert also
a:=matrix([-26,2]):
at:=linalg::transpose(a)
![]()
atb:=at*P
![]()
kegSD:=ew1*x^2+ew2*y^2+atb[1]*x+atb[2]*y+59
![]()
kegSDp:=plot::Implicit2d(kegSD=0,x=-8..7,y=-4..4,
LineWidth=1,LineColor=[0,1,0],GridVisible=TRUE):
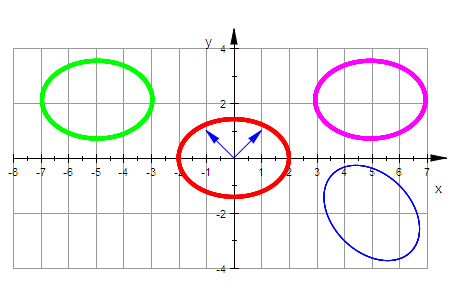
plot(kegp,kegSDp, kegHp,ev1p,ev2p,Scaling=Constrained)
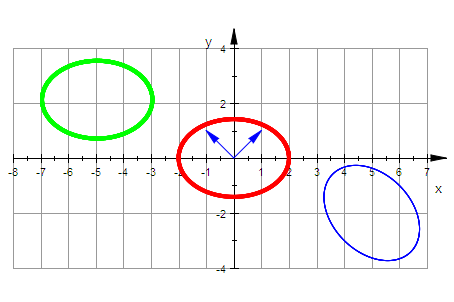
Bei der Betrachtung dieses Bildes fällt auf, dass es sich nicht allein um eine
Drehung handelt, sondern dass offenbar noch eine Spiegelung im Spiel ist.
Es kann eine positive Drehung und eine Spiegelung an der y-Achse sein.
Pt, float(Pt);
Dr:=phi->matrix([[cos(phi),-sin(phi)],[sin(phi),cos(phi)]]): Dr(`ϕ`);

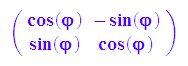
Der Vergleich mit der allgemeinen Drehmatrix ergibt, dass es mit alleinigem Drehen nicht geht.
Spy:=matrix([[-1,0],[0,1]]);
Spy*Dr(`ϕ`) //Spiegeung an der y-Achse

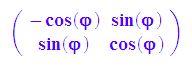
Das kann man anpassen:
cos(phi)=-float(Pt[1,1]);sin(phi)=float(Pt[2,1]);
![]()
![]()
In diesem Fall sieht man gleich, dass es sich um eine 45°-Drehung handelt.
arccos((-Pt[1,1]));
wi:=arcsin((Pt[2,1]));
![]()
![]()
Daraus folgt umgerechnet ins Winkelmaß (hier klar):
float(arccos(-(Pt[1,1]))/PI*180);
wi:=float(arcsin((Pt[2,1]))/PI*180);
![]()
![]()
So passt es auch zur Zeichnung.
Einzeichnen des Zwischenbildes:
p:=matrix([x,y]);
pt:=linalg::transpose(p);
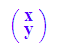
![]()
Beachte, dass die inverse Drehung die ist, die um den negativen Winkel dreht.
kegD:=simplify(pt*Dr(wi)*A*Dr(-wi)*p+at*Dr(-wi)*p+59);
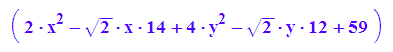
Dieses hätte man auch als transformierte Gleichung erhalten, wenn man die Eigenvektoren
anders herum nummeriert hätte. Dann wäre Pt = Dr(wi) gewesen.
kegDp:=plot::Implicit2d(kegD[1],x=-8..7,y=-4..4,
LineWidth=1,LineColor=[1,0,1],GridVisible=TRUE):
plot(kegp,kegSDp,kegDp, kegHp,ev1p,ev2p,Scaling=Constrained)
##############################
Bestimmung der Translation:
kegSD
![]()
Die Arbeitsweise ist dieselbe wie bei der Herstellung der Scheitelform einer Parabel.
Hier durch Hinsehen:
xterm:=hold(2*(x+7/2*sqrt(2))^2);expand(xterm);
yterm:=hold(4*(y-3/2*sqrt(2))^2);expand(yterm);
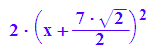
![]()
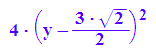
![]()
Also
kegSDK:=xterm+yterm-d1
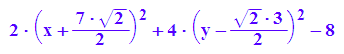
Letzter Teil der Hauptachsentransformation ist die Translation t
t:=matrix([7/2*sqrt(2), -3/2*sqrt(2)])
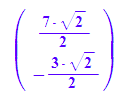
also
Das ergibt:
ew1*x^2+ew2*y^2-8
![]()
Angabe der Gelichung in der üblichen Form:
hold(x^2/4+y^2/2=1)
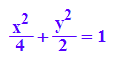
Bestimmung des ursprünglichen Mittelpunktes:
m:=P*(-t)
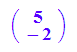
Bestimmung des Urbildes des rechten Hauptscheitels:
Mit ev1 rechts ist hier der normierte 1. Eigenvektor gemeint.
r:=2: //große (rechte) Halbachse
rur:=r*ev1n+m;
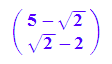
mp:=plot::Point2d(m):
rurp:=plot::Point2d(rur):
rp:=plot::Point2d([r,0]):
ev1urp:=plot::Arrow2d(m,m+ev1):
ev2urp:=plot::Arrow2d(m,m+ev2):
tp:=plot::Arrow2d(-t,[0,0]):
plot(kegp,kegSDp,kegDp, kegHp,mp,rurp,rp,tp,
ev1urp,ev2urp,PointSize=2,Scaling=Constrained)