A:= matrix([[1,-4],[-4,5]])
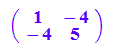
Hyperbel in allgemeiner Lage
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4 Juni 07 Update 29.06.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
##############################################
Sinnvoller ist die Erzeugung mit "Konstruktion rückwärts-2d"
##############################################
Das Beispiel aus der Vorlesung, mit Eigenwerten, die Wurzelausdrücke sind.
So hatten wir es uns die Matrix A ausgedacht. Rechnerisch ist das also kein günstiges Beispiel.
Konsequenz dieser Erfahrung sind die Dateien zur Rückwärtskonstrunktion der Kegelschnitte
und Quadriken.
A:= matrix([[1,-4],[-4,5]])
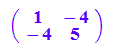
keg:=A[1,1]*x^2+2*A[1,2]*x*y+A[2,2]*y^2-5
![]()
kegp:=plot::Implicit2d(keg,x=-5..8,y=-2..2):
plot(kegp,Scaling=Constrained);
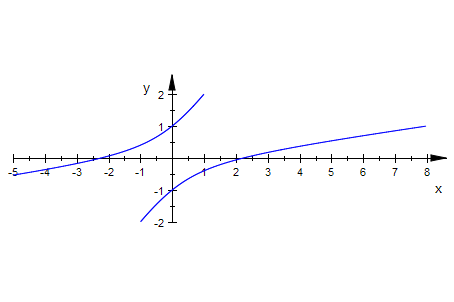
Dieser Kegelschnitt ist offenbar eine Hyperbel.
Bestimmung der Achsenrichtungen:
evli:=linalg::eigenvectors(A)
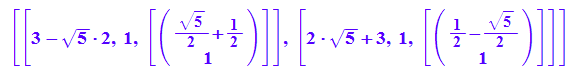
ev1:=evli[1][3][1];
ev2:=evli[2][3][1];
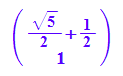
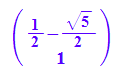
float(ev1),float(ev2)
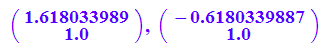
Das folgende hatten wie in der Vorlesung zu vx=1 selbst berechnet
vy:=float(-1/2+sqrt(20)/4)
![]()
Das passte also.
Einzeinenen der Eigenvektoren:
ev1p:=plot::Arrow2d(ev1):
ev2p:=plot::Arrow2d(ev2):
plot(kegp,ev1p,ev2p, Scaling=Constrained)
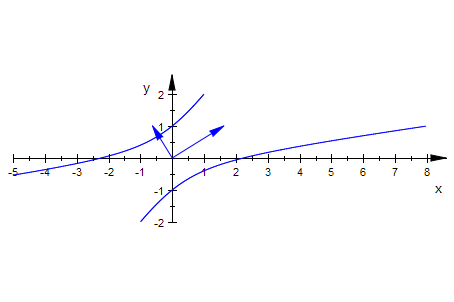
Wie erwartet sind die Eigenvektoren die Richtungen der Hauptachsen des Kegelschnittes.
---------------------------------------------------
Bestimmung der Kegelschnittgleichung ist ganz einfach, wenn man die Theorie gleich verwendet:
Man nimmt die Eigenwerte als Koeffizienten der quadratischen Glieder.
Die gemischten lässt man weg.
Wie eventuelle lineare Glieder umgeformt werden, wird in anderen Beispielen gezeigt.
ew1:=evli[1][1];
ew2:=evli[2][1];
![]()
![]()
kegH:=ew1*x^2+ew2*y^2-5;
float(%)
![]()
![]()
Diesen in Hauptachsenlage transformierten Kegelschnitt
zeichnen wir ein:
kegHp:=plot::Implicit2d(kegH,x=-5..8,y=-2..2,
LineWidth=1,LineColor=[1,0,0]):
plot(kegp, kegHp,ev1p,ev2p,Scaling=Constrained)
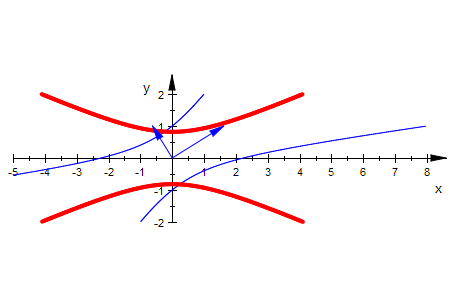
Ganz offenbar ist da eine Drehung vollzogen worden.
Die Drehmatrix von der Hauptachsenlage in die gegebene Lage ergibt sich aus den normierten Eigenvektoren.
Die stehen gleich von alleine senkrecht aufeinander, wenn die Eigenwerte verschieden sind.
Sie ist dann eine Orthonormal-Matrix, bezeichnet mit P. Für solche ist die inverse Matrix
gleich der transponierten Matrix, bezeichnet mit Pt (oder mit hochstelltem T).
Die Transformationsmatrix, die den Kegelschnitt in die Hauptachsenlage dreht, ist Pt.
Abbildungsgleichung:
Die Theorie sagt nun, dass Pt*A*P die Diagonalmatrix aus den Eigenwerten ist.
Davon kann man sich hier überzeugen:
ev1n:=linalg::normalize(ev1):
ev2n:=linalg::normalize(ev2):
P:=ev1n.ev2n
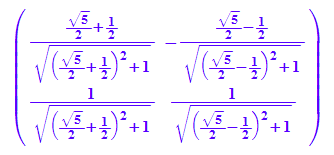
float(P)

Pt:=linalg::transpose(P)
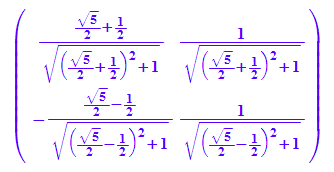
float(Pt)

Der Vergleich mit der allgemeinen Drehmatrix ergibt:
cos(phi)=float(Pt[1,1]);sin(phi)=float(Pt[2,1]);
![]()
![]()
Daraus folgt umgerechnet ins Winkelmaß:
float(arccos(float(Pt[1,1]))/PI*180);
wi:=float(arcsin(float(Pt[2,1]))/PI*180);
![]()
![]()
Die Deutung muss man etwas überlegen, mit
wi
![]()
sind beide Gleichungen erfüllt. Also ist es eine Drehung um diesen Winkel.
So passt es auch zur Zeichnung.
Diagonalisierung, die klappt immer, wenn die EV eine ONB bilden,
wenn man also so ein P aufstellen kann.
Simplify(Pt*A*P);
float(Pt*A*P)
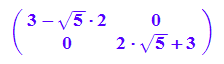
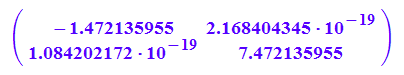
Die winzigen 10^-19 Werte sind numerisch 0.