E2:=matrix([[1,0],[0,1]])
Kegelschnitte Konstruktion rückwärts 2d
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Juli 07 Update 11.07.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Mit Konstruktion einer anderenLage, Sammlung guter Beispiele, unten
-----------------------------
E2:=matrix([[1,0],[0,1]])
Gewünschte orthogonale EV
//v1:=matrix([1,2]);
//v2:=matrix([-2,1]);
v1:=matrix([3,-1]);
v2:=matrix([1,3]); //selbst aufpassen, dass dieser orthogonal ist.
linalg::scalarProduct(v1,v2)
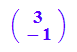
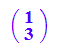
![]()
v1n:=linalg::normalize(v1):
v2n:=linalg::normalize(v2):
Pv:=v1n.v2n
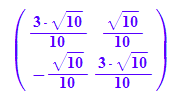
simplify(linalg::det(Pv))
![]()
Sollte diese Determinante kann -1 sein, vertauscht man besser die EV, da sonst später außer
einer Drehung noch eine Spigelung im Spiel ist.
Ptv:=linalg::transpose(Pv)
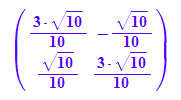
kv1:=3: kv2:=2: // freie Wahl der EW, verschieden
//kv1:=1: kv2:=kv1 // freie Wahl des dopp. EW
//trivial, zentrische Streckung
Dewv:=matrix([[kv1,0],[0,kv2]])
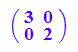
A:=Simplify(Pv*Dewv*Ptv);
5*Pv*Dewv*Ptv

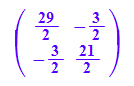
amke:={A-kv1*E2, A-kv2*E2} //Verwendung bei Berechnung es EV
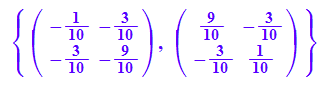
Simplify(map(amke,linalg::det)) //Probe
![]()
evli:=linalg::eigenvectors(A) //Probe, was MuPAD liefert
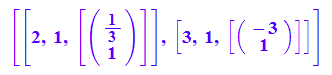
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
####################################################################
Gehe zum passenden Fall
Anpassen wegen der Vielfachheiten Fall1 Zwei verschiedene EW
k1 :=evli[1][1]; k2 :=evli[2][1];
ev1:=evli[1][3][1];
ev2:=evli[2][3][1];
![]()
![]()
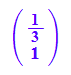
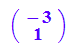
linalg::det(ev1.ev2)
![]()
##################################################################
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
Anpassen wegen der Vielfachheiten Fall 2 ein doppelter EW.
Zentrische Steckung
//k1 :=evli[1][1]; k2 :=evli[1][1];
//ev1:=evli[1][3][1];ev2:=evli[1][3][2];
![]()
![]()
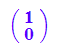
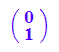
#########################################
Konstruktion einer anderen Lage
p:=matrix([x,y]): pt:=linalg::transpose(p)
![]()
Erfindung des Mittelpunktes für das Urbild
m:=matrix([-4,3]); mt:=linalg::transpose(m) ;
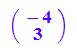
![]()
Konstruktion ein schönen Quadrik-Gleichung
d:=-kv1*kv2; // das ist nicht nötig aber praktisch
Keg1:=10*expand((pt-mt)*A*(p-m)+d);
![]()
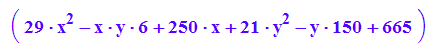
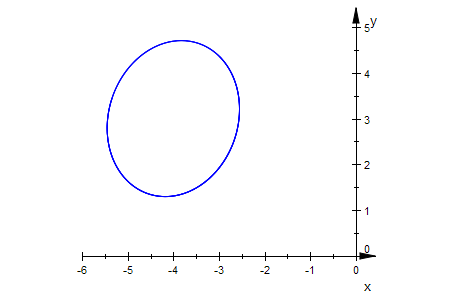
Keg1p:=plot::Implicit2d(Keg1[1]=0,x=-6..0,y=0..5):
plot(Keg1p,Scaling=Constrained):
##############################################################
Sammlung guter Beispiele,
v1:=matrix([1,2]);
v2:=matrix([-2,1]); //selbst aufpassen, dass dieser orthogonal ist.
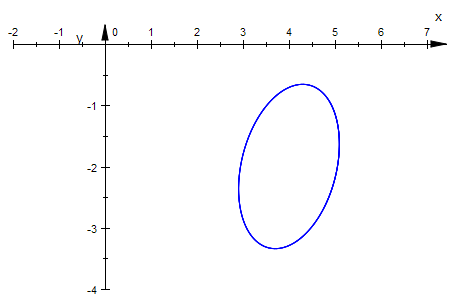
Ellipse
kv1:=1: kv2:=2: // freie Wahl der EW, verschieden
Keg1:=matrix([[9*x^2 - 4*x*y - 80*x + 6*y^2 + 40*y + 190]])
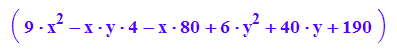
m:=matrix([4,-2]);
Keg1p:=plot::Implicit2d(Keg1[1]=0,x=-2..7,y=-4..0):
plot(Keg1p):
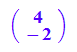
Hyperbel
d:=-kv1*kv2; // das ist nicht nötig aber praktisch
Keg2:=5*expand((pt-mt)*A*(p-m)+d);
![]()
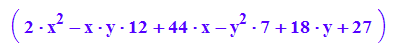
Keg2p:=plot::Implicit2d(Keg2[1]=0,x=-8..8,y=-4..10):
plot(Keg1p,Scaling=Constrained):
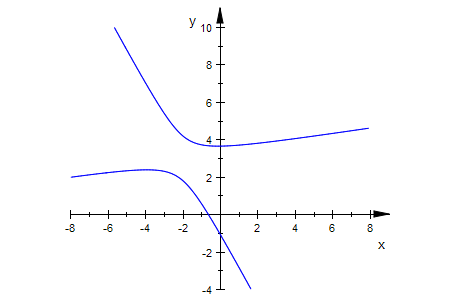
Parabel Beispiel 1
Keg5:=matrix([[x^2 + 4*x*y + 4*x + 4*y^2 + 18*y + 34]]);
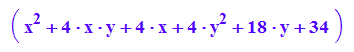
Keg5p:=plot::Implicit2d(Keg5[1]=0,x=-1..8,y=-8..1):
plot(Keg5p,Scaling=Constrained):
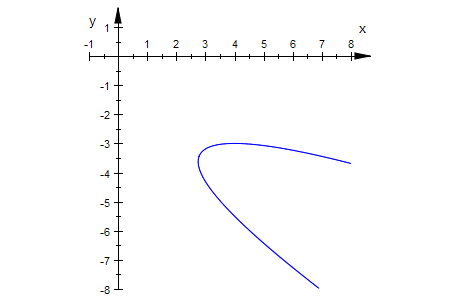
Parabel Beispiel 2
Keg3:=matrix([[8*x^2 - 8*x*y + 24*x + 2*y^2 - 32*y - 12]])
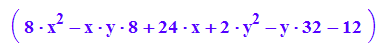
Keg3p:=plot::Implicit2d(Keg3[1]=0,x=-8..8,y=-4..10):
plot(Keg3p,Scaling=Constrained):
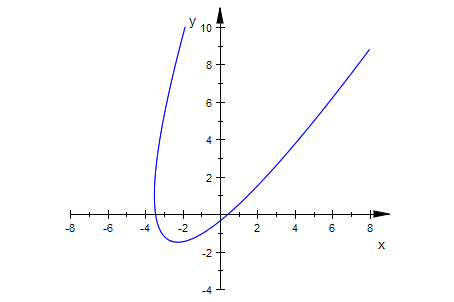
Weitere Ellipse, dann als Einführung genommen
v1:=matrix([3,-1]);
v2:=matrix([1,3]);
kv1:=3: kv2:=2: // freie Wahl der EW, verschieden
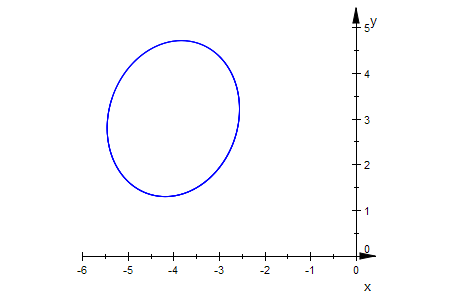
Keg4:=matrix([[29*x^2 - 6*x*y + 250*x + 21*y^2 - 150*y + 665]])
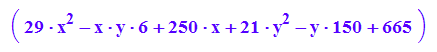
Keg4p:=plot::Implicit2d(Keg4[1]=0,x=-6..0,y=0..5):
plot(Keg4p,Scaling=Constrained):