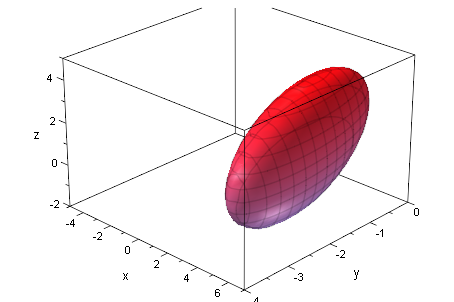
E3:=matrix([[1,0,0],[0,1,0],[0,0,1]])

Quadriken Konstruktion rückwärts 3d
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Juni 07 Update 30.06.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Fall1 drei verschiedene EW
Fall2 zwei verschiedene EW, einer doppelt
Konstruktion einer anderenLage, Sammlung guter Beispiele, unten
-----------------------------
E3:=matrix([[1,0,0],[0,1,0],[0,0,1]])

Gewünschte orthogonale EV
v1:=matrix([1,-1,1]);
v2:=matrix([-1,1,2]); //selbst aufpassen, dass dieser orthogonal ist.
v3:=1/3*linalg::crossProduct(v1,v2);
linalg::scalarProduct(v1,v2)
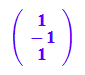
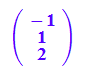
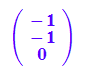
![]()
v1n:=linalg::normalize(v1):
v2n:=linalg::normalize(v2):
v3n:=linalg::normalize(v3):
Pv:=v1n.v2n.v3n

simplify(linalg::det(Pv))
![]()
Diese Determinantet kann eigentlich wegen des Kreuzproduktes nicht -1 werden.
Falls man von Hand aufgestellt hat und diese Det. -1 ist, vertauscht man besser v1 und v2.
Anderenfalls ist noch eine Achsenspiegelung nach der Drehung zu denken.
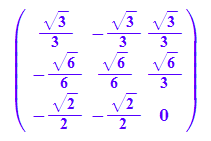
Ptv:=linalg::transpose(Pv)
kv1:=2: kv2:=1: kv3:=4: // freie Wahl der EW, verschieden
//kv1:=1: kv2:=2: kv3:=kv2: // freie Wahl der EW, einer dopp
//kv1:=2: kv2:=kv1:kv3:=kv1: // freie Wahl des dreifachen EW, trivial, zentrische Streckung
Dewv:=matrix([[kv1,0,0],[0,kv2,0],[0,0,kv3]])

A:=Simplify(Pv*Dewv*Ptv);
factor(Simplify(Pv*Dewv*Ptv))

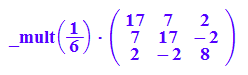
amke:=[A-kv1*E3, A-kv2*E3,A-kv3*E3] //Verwendung bei Berechnung es EV

Simplify(map(amke,linalg::det)) //Probe
![]()
evli:=linalg::eigenvectors(6*A) //Probe, was MuPAD liefert
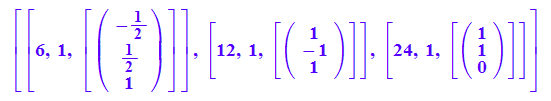
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
####################################################################
Gehe zum passenden Fall
Anpassen wegen der Vielfachheiten Fall1 Drei verschiedene EW
k1 :=evli[1][1]; k2 :=evli[2][1]; k3 :=evli[3][1];
ev1:=evli[1][3][1]:
ev2:=evli[2][3][1]: //evt. neg, damit Rechtssystem herauskommt
ev3:=evli[3][3][1]:
![]()
![]()
![]()
linalg::det(ev1.ev2.ev3)
![]()
Diese Determinante sollte positiv sein, donst ist später noch eine
Spiegelung im Spiel.
##################################################################
Herausgreifen der EigenWerte ki und der Eigenvektoren evi
Anpassen wegen der Vielfachheiten Fall 2 zwei verschiedene EW, ein dopp.
//k1 :=evli[1][1]; k2 :=evli[1][1]; k3 :=evli[2][1];
//ev1:=evli[1][3][1];ev2:=evli[1][3][2];ev3:=evli[2][3][1];
![]()
![]()
![]()
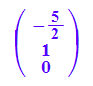
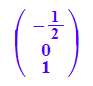
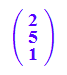
Hier müssen später die EV orthogonalisiert werden, z.B.
//ev1:=linalg::crossProduct(ev2,ev3)

linalg::det(ev1.ev2.ev3)
![]()
Diese Determinante sollte positiv sein, donst ist später noch eine
Spiegelung im Spiel.
#########################################
Konstruktion einer anderen Lage
p:=matrix([x,y,z]): pt:=linalg::transpose(p)
![]()
Erfindung eines Punktes für das Urbild.
Bei parabolischen Quadriken ist die vorherige Bestimmung des Scheitels
an dieser Stelle zu aufwändig. Ist kein Eigenwert 0 kann man hier einen Mittelpunkt
der späteren Quadrik wählen.
m:=matrix([5,-2,2]); mt:=linalg::transpose(m) ;
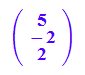
![]()
Konstruktion ein schönen Quadrik-Gleichung.
Bei parabolischen Quadriken muss hier ein linearer Term für die
Richtung mit Eigenwert 0 ( Reihenfolge von MuPAD) vorgesehen werden.
z.B.
d:=-kv1*kv2*kv3; // das ist nicht nötig aber praktisch
Quadrik:=6*expand((pt-mt)*A*(p-m)+d);
![]()
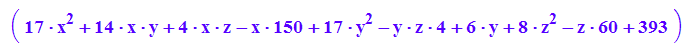
Qp:=plot::Implicit3d(Quadrik[1]=0,x=-5..7,y=-4..0,z=-2..5
,Mesh=[20,20,20]):
plot(Qp):
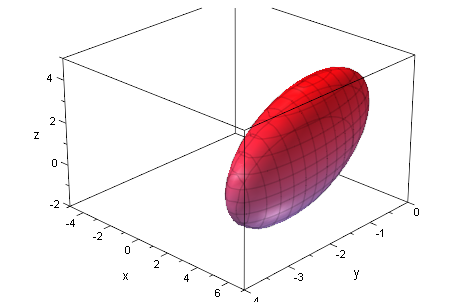
##############################################################
Sammlung guter Beispiele,
v1:=matrix([1,1,2]);
v2:=matrix([-1,-1,1]); //selbst aufpassen, dass dieser orthogonal ist.
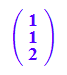
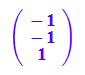
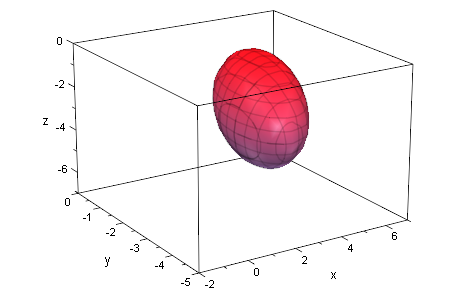
Ellipsoid, in Extradatei dann untersucht
kv1:=1: kv2:=2: kv3:=3: // freie Wahl der EW, verschieden
Q1:=matrix([[7*x^2 - 4*x*y - 2*x*z - 70*x + 7*y^2 - 2*y*z + 38*y + 4*z^2 + 28*z + 202]])
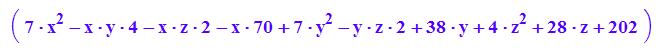
m:=matrix([4,-2,-3]);
Q1p:=plot::Implicit3d(Q1[1]=0,x=-2..7,y=-5..0,z=-7..0):
plot(Q1p):
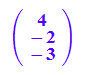
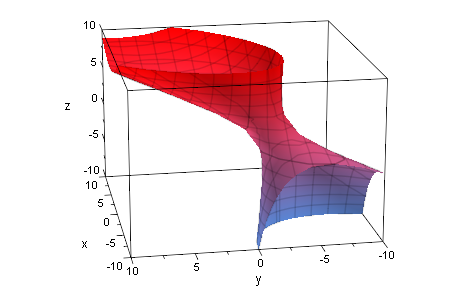
Einschaliges Hyperboloid
Q2:=matrix([[42*z - 6*y - 60*x - 6*x^2 - 6*y^2 + 6*x*y + 6*x*z + 6*y*z - 180]])
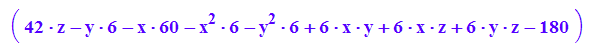
m:=matrix([-5,-2,2]):
Q2p:=plot::Implicit3d(Q3[1]=0,x=-10..10,y=-10..10,z=-10..10):
plot(Q2p):
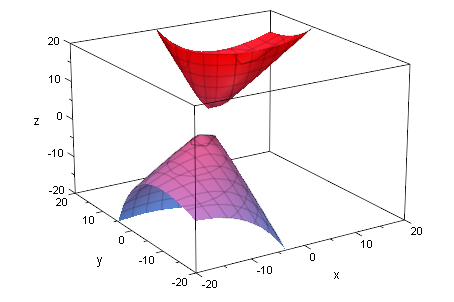
zweischaliges Hyperboloid
Q3:=matrix([[78*x - 30*y - 12*z + 6*x^2 + 6*y^2 - 6*x*y - 6*x*z - 6*y*z + 222]])
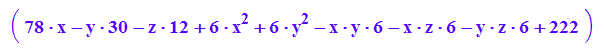
m:=matrix([-4,2,3]):
Q3p:=plot::Implicit3d(Q3[1]=0,x=-20..20,y=-20..20,z=-20..20):
plot(Q3p):
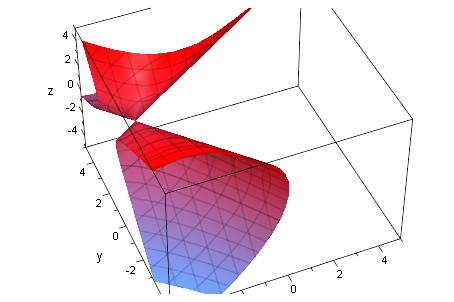
Kegel
EW:=[1,3,-2]: m:=[-4,1,2]: //liegt drauf, Mittelpnkt
Quadrik5:=matrix([[33*x^2 - 24*x*y - 42*x*z + 372*x - 30*y^2 - 24*y*z + 12*y + 33*z^2 - 276*z + 1014]]);
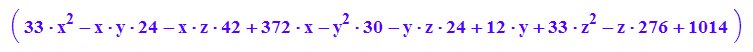
Q5p:=plot::Implicit3d(Quadrik5[1]=0,x=-5..5,y=-5..5,z=-5..5):
plot(Q5p):
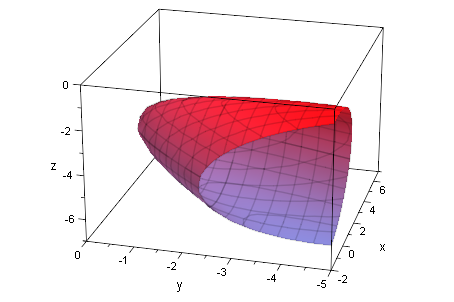
Elliptisches Paraboloid
EW:=[0,1,2]: m:=[3,-1,-3] //liegt drauf
Quadrik7:=matrix([[5*x^2 - 10*x*y - 4*x*z - 40*x + 5*y^2 + 4*y*z + 52*y + 8*z^2 + 64*z + 164]]);
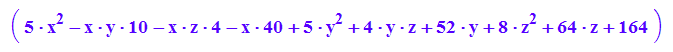
Quadrik7|{x=3,y=-1,z=-3}
![]()
Q7p:=plot::Implicit3d(Quadrik7[1]=0,x=-2..7,y=-5..0,z=-7..0):
plot(Q7p):
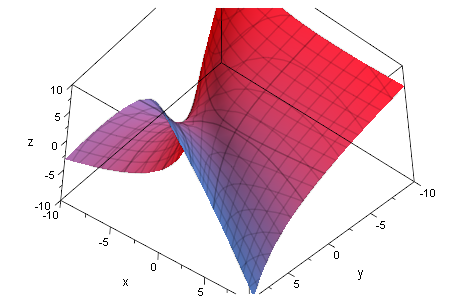
Hyperbolisches Paraboloid
EW:=[0,-2,1]: m:=[-3,1,-3]; //liegt drauf
Quadrik8:=matrix([[60*y + 48*z - 3*x^2 - 3*y^2 + 6*x*y + 12*x*z - 12*y*z - 12]])
![]()
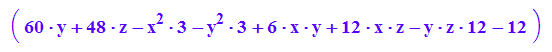
Quadrik8|{x=-3,y=1,z=-3}
![]()
Q8p:=plot::Implicit3d(Quadrik8[1]=0,x=-10..10,y=-10..10,z=-10..10):
plot(Q8p):
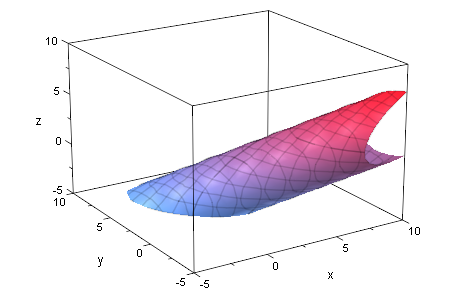
Elliptischer Zylinder
EW:=[0,3,2]: m:=[4,2,-2]://Mittelpunkt
Quadrik9:=matrix([[11*x^2 + 8*x*y - 14*x*z - 132*x + 8*y^2 + 8*y*z - 48*y + 11*z^2 + 84*z + 288]]);
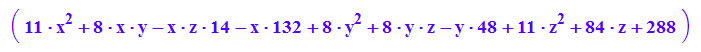
Q9p:=plot::Implicit3d(Quadrik9[1]=0,x=-5..10,y=-5..10,z=-5..10):
plot(Q9p):
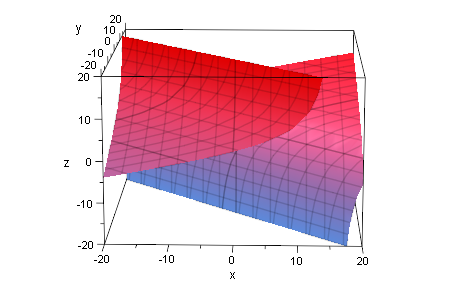
Hyperbolischer Zylinder, in Extradatei dann untersucht
Q10:=matrix([[8*z - 12*y - 12*x - 1/2*x^2 - 1/2*y^2 - x*y + 2*x*z + 2*y*z + 40]])
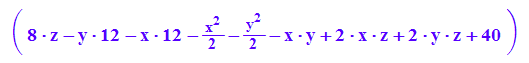
m:=matrix([-1,-3,4]):
Q10p:=plot::Implicit3d(Q10[1]=0,x=-20..20,y=-20..20,z=-20..20):
plot(Q10p):
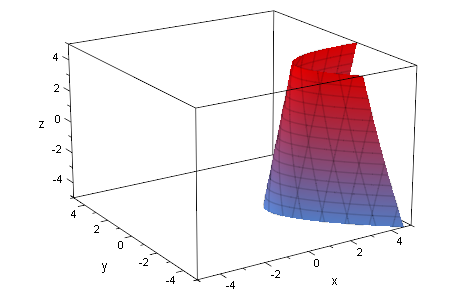
Parabolischer Zylinder
Quadrik14:=matrix([[4*x^2 + 20*x*y + 4*x*z - 36*x + 25*y^2 + 10*y*z + 60*y + z^2 + 12*z + 96]]);
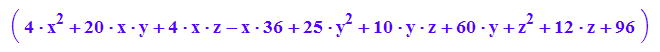
Q14p:=plot::Implicit3d(Quadrik14[1]=0,x=-5..5,y=-5..5,z=-5..5,
Mesh=[20,20,20]):
plot(Q14p):
ein weiteres Ellipsoid
EW:=[6,12,24]: m:=[5,-2,2]://Mittelpunkt
Quadrik1b:=6*expand((pt-mt)*A*(p-m)+d);
![]()
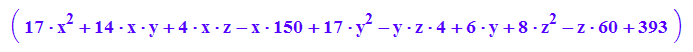
Q1bp:=plot::Implicit3d(Quadrik1b[1]=0,x=-5..7,y=-4..0,z=-2..5
,Mesh=[20,20,20]):
plot(Q1bp):