p:=matrix([x,y,z]):pt:=linalg::transpose(p)
![]()
Quadriken 3d Hyperbolisches Paraboloid
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Juni 07 Update 30.06.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Rückwärts aufgestellt, siehe Datei Konstruktion-rückwärts
p:=matrix([x,y,z]):pt:=linalg::transpose(p)
![]()
Hyperbolisches Paraboloid
//kv1:=0: kv2:=-2: kv3:=3:
quadrik:=matrix([[5*x^2 - 26*x*y + 8*x*z - 88*x + 5*y^2 + 8*y*z + 56*y - 4*z^2 + 34*z + 128]])
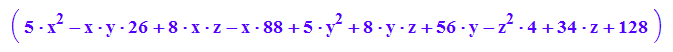
quadrikp:=plot::Implicit3d(quadrik[1]=0,x=-5..5,y=-10..2,z=-5..5,FillColor=[0,1,0,1], Scaling=Constrained):
plot(quadrikp):
quadrikp:=plot::Implicit3d(quadrik[1]=0,x=-5..5,y=-10..2,z=-5..5,FillColor=[0,1,0,0.8], Scaling=Constrained): //nochmal Transparent
A passend aufstellen
A:=matrix([[5,-13,4],[-13,5,4],[4,4,-4]]);
a:=matrix([-88,+56,34]): at:=linalg::transpose(a);
d:=128;
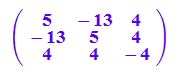
![]()
![]()
expand(pt*A*p+at*p+d); //Probe, ob man A,a und d richtig hat
%-quadrik
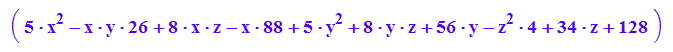
![]()
hier muss 0 herauskommen
Hauptachtsentransformation
E3:=matrix([[1,0,0],[0,1,0],[0,0,1]])

evli:=linalg::eigenvectors(A) //Probe, was MuPAD liefert
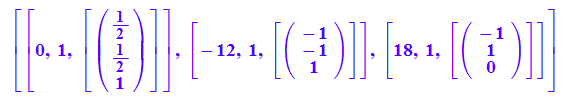
Eigenwerte und Eigenvektoren
ew1 :=evli[1][1]; ew2 :=evli[2][1]; ew3 :=evli[3][1];
ev1:=evli[1][3][1]:
ev2:=evli[2][3][1]:
ev3:=evli[3][3][1]:
![]()
![]()
![]()

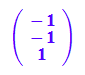
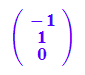
ev1n:=linalg::normalize(ev1):
ev2n:=linalg::normalize(ev2):
ev3n:=linalg::normalize(ev3):
P:=ev1n.ev2n.ev3n: Pt:=linalg::transpose(P);
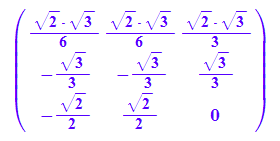
Vektorschreibweise für die Abbildung und die
Quadrikgleichungen, die sich durch Einsetzen ergeben:
bzw. in 3D
quastrich:=Simplify(pt*Pt*A*P*p+at*P*p+d)
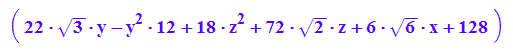
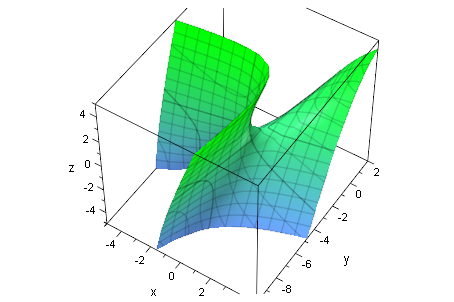
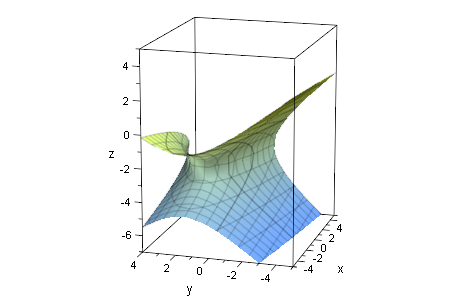
quastrichp:=plot::Implicit3d(quastrich[1],x=-5..5,y=-5..4, z=-7..5,FillColor=[1,1,0,1]):
plot(quastrichp /*,Op, tp */, Scaling=Constrained):
quastrich
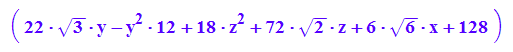
Die Arbeitsweise ist dieselbe wie bei der Herstellung der Scheitelform einer Parabel.
Hier durch Hinsehen:
//xterm:=hold(6*(x+5/3*sqrt(3))^2);expand(xterm);
yterm:=hold(-12*(y-11/12*sqrt(3))^2);expand(yterm);
zterm:=hold(18*(z+2*sqrt(2))^2);expand(zterm);
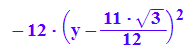
![]()
![]()
![]()
Also
128-(144-121/4)
![]()
xterm:=6*sqrt(6)*(x+57/(24*sqrt(6)));expand(xterm);
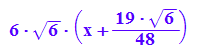
![]()
quastrichK:=xterm+yterm+zterm
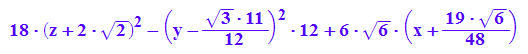
quastrich-expand(quastrichK)
![]()
hier muss 0 herauskommen
Letzter Teil der Hauptachsentransformation ist die Translation t
t:=matrix([19*sqrt(6)/48, -11/12*sqrt(3),2*sqrt(2)]);
tt:=linalg::transpose(t):

also
Das ergibt:
quaH:=Simplify(expand((pt-tt)*Pt*A*P*(p-t)+at*P*(p-t)))+6*sqrt(x)+128;
quadrikH:=ew1*x^2+ew2*y^2+ew3*z^2+6*sqrt(6)*x;
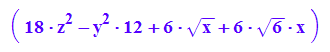
![]()
Angabe der Gleichung in der üblichen Form:
hold(x/sqrt(6)-y^2/3+z^2/2=0)
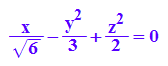
quadrikHp:=plot::Implicit3d(quadrikH,x=-2..2,y=-3..3, z=-2..2,
Scaling=Constrained):
plot(%)
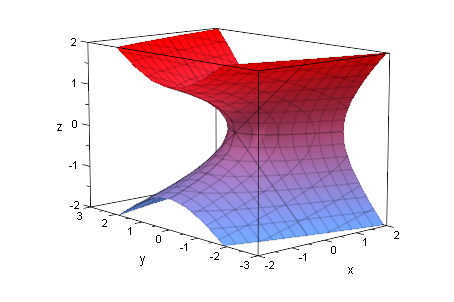
Bestimmung des ursprünglichen Mittelpunktes:
nun in 3D
m:=Simplify(P*(-t))
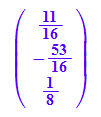
Dieses ist der alte Mittelpunkt.
Bestimmung des Urbildes des rechten Hauptscheitels:
Mit ev1 rechts ist hier der normierte 1. Eigenvektor gemeint. Alles jetzt in 3D
r:=matrix([-2/3*sqrt(6),2,2]): //Punkt auf letzem Bild
rurstr:=r-t;
rur:=float(P*rurstr);
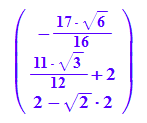

r
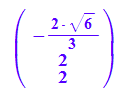
mp:=plot::Point3d(m,PointSize=2, PointColor=[0,1,0]):
Op:=plot::Point3d([0,0,0], PointSize=2, PointColor=[1,0,0]):
rurp:=plot::Point3d(rur, PointSize=2, PointColor=[0,1,1]):
rursp:=plot::Point3d(rurstr, PointSize=2, PointColor=[1,0.5,0]):
rp:=plot::Point3d(r,PointSize=2, PointColor=[0,0,1]):
ev1urp:=plot::Arrow3d(m,m+3*ev1):
ev2urp:=plot::Arrow3d(m,m+3*ev2):
ev3urp:=plot::Arrow3d(m,m+3*ev3):
tp:=plot::Arrow3d(-t,[0,0,0],LineColor=[1,0,0]):
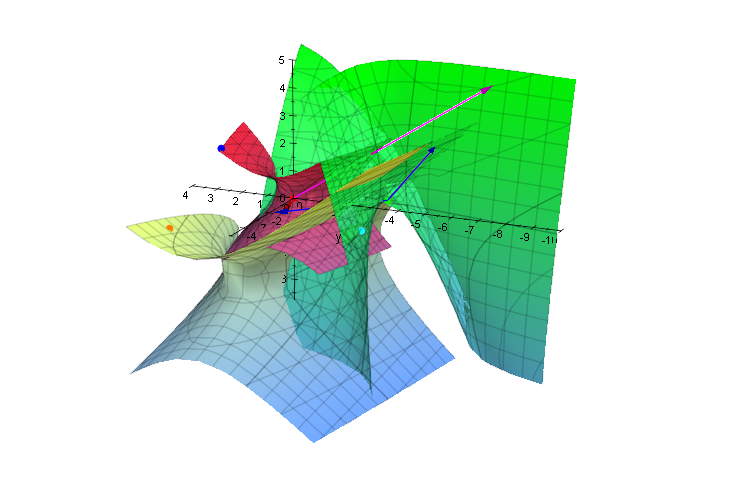
plot(quadrikp,mp,Op,rurp,tp,
ev1urp,ev2urp,ev3urp,PointSize=2,Scaling=Constrained);
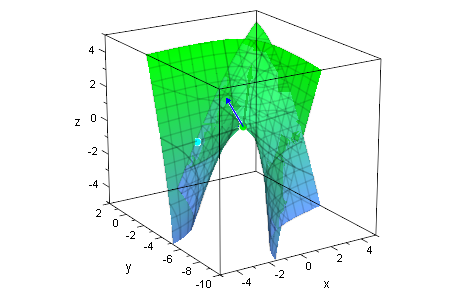
Test ob es eine Drehung allein oder gefolgt von Spiegelung ist. det=1 reine Drehung
linalg::det(Pt)
![]()
plot(quadrikp,quastrichp, quadrikHp,mp,Op,tp,rp,rurp,rursp,
ev1urp,ev2urp,ev3urp,Axes=Origin,Scaling=Constrained)
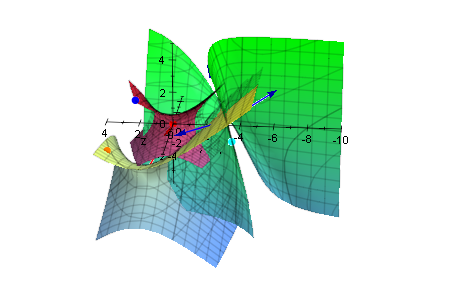
Bestimmung der Dreh-Spiegelachse
Pt
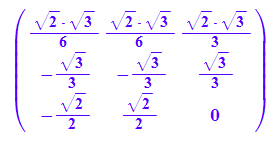
evliP:=linalg::eigenvectors(Pt)
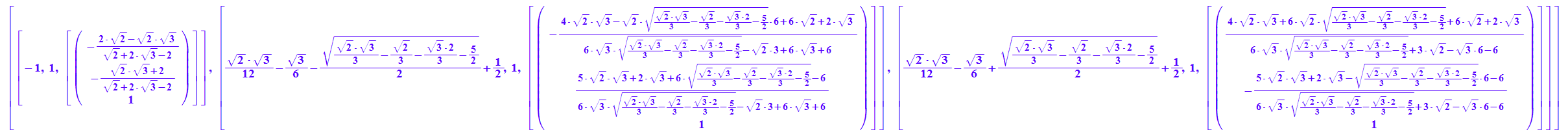
float(evliP)

dreh:=evliP[1][3][1]
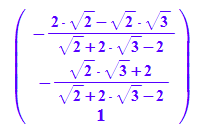
drehp:=plot::Arrow3d(5*dreh, LineColor=[1,0,1])
plot(quadrikp,quastrichp, quadrikHp,mp,Op,tp,rp,rurp,rursp,
ev1urp,ev2urp,ev3urp,drehp,Axes=Origin,Scaling=Constrained)