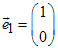
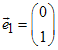
Affine Abbildungen Drehungen, Spiegelungen...
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Okt. 05 Update 27.10.05
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Dieses Notebook eignet sich für viele Beispiele. "Grün" muss angepasst werden. (3 Stellen) ######################################################
Die Spalten der Abbildungsmatrix sind Bilder von 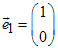
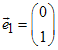
Eh:=matrix([[1,0],[0,1]])
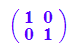
Drehung um Ursprung mit Winkel phi
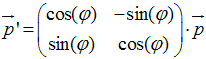
Dr:=phi-> matrix([[cos(phi), -sin(phi)], [sin(phi), cos(phi)]]):
Dr(phi)
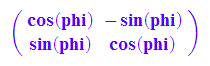
Spiegelung an der x-Achse
Spx:=matrix(
[[1,0],[0,-1]]);

Spiegelung an der y-Achse
Spy:=matrix([[-1,0],[0,1]]);
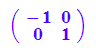
Spiegelung an der Ursprungs-Geraden y=m x
gw= Steigungswinkel in RAD.
gw:=arctan(m);

Spm:=Dr(gw)*Spx*Dr(-gw)
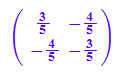
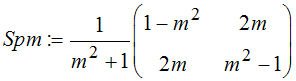
----------------------------
Von Hand ginge das so:
Dr(g)*Spx*Dr(-g);
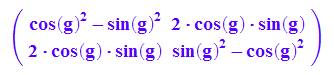
Additionstheoreme
expand(sin(2*t)),expand(cos(2*t));
![]()
combine(cos(t)^2-sin(t)^2,sincos);
combine(2*cos(t)*sin(t),sincos);
![]()
![]()
rewrite(cos(2*g),tan);
rewrite(sin(2*g),tan)
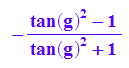
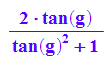
mit tan(g)=m erhält man dann die angegebene Matrix
----------------------------------
gw= Steigungswinkel in RAD.
Spmw:=matrix([[cos(2*gw),sin(2*gw)],[sin(2*gw),-cos(2*gw)]])
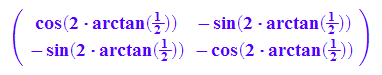
---------------------------------------------------------------------
Spiegelung an der Geraden y=m x+b
bvec:=matrix([0,b])
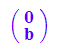
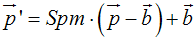
------------------------------------------------------------------------
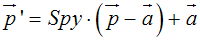
-------------------------------------------------------------------------
Zentrische Streckung von Ursprung aus mit Faktor k
Zk:=k*Eh;
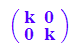
--------------------------------------------------------------------------
Scherung mit y-Achse als Scherachse , Steigungswinkel von Steigung m als Scherwinkel
Scher:=matrix([[1,0],[-m,1]])
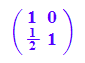
fkt:=matrix([x,f(x)])
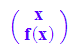
Scher*fkt
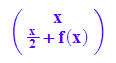
Hier sieht man, dass solche Scherungen Additionen von Ursprungsgeragen sind.
+++++++++++++++++++++++++++++++++++++++++++++
Definition eines Urbildes , hier eintragen
myUr:=[[2,0],[2,1],[1,1],[1,3],[0,3],[0,0],[2,0],[1,1/2]]:
myUrM:=linalg::transpose(matrix(myUr))

npk:=nops(myUr): //Anzahl der Punkte
++++++++++++++++++++++++++++++++++++++++++++++++
Verschiebung
Translationsvektor hier eintragen Weiterer Hilfsvektor a hier eintragen
trans:=matrix([0,0]);
avec:=matrix([a,b]);
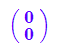
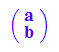
Aufblasen der Translationsvektoren zu Matrizen (als Funktion)
tm:=tr->linalg::transpose(matrix([[tr[1],tr[2]] $ npk])):
tm(trans);
tm(avec);

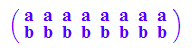
Auswahl, welche Abbildung gezeichnet werden soll. Aktiviere durch Anpassen und Fortnehmen der //
//A:=Dr(PI/3);// hier Drehwinkel eintragen
//A:=Spx;
A:=Spm; m:=-1/2 // hier m eintragen
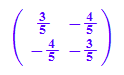
![]()
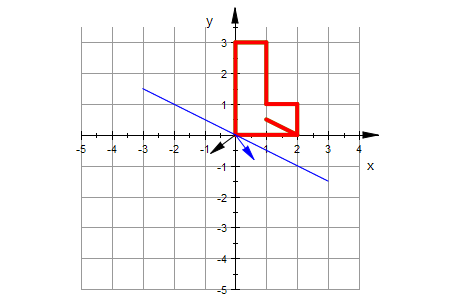
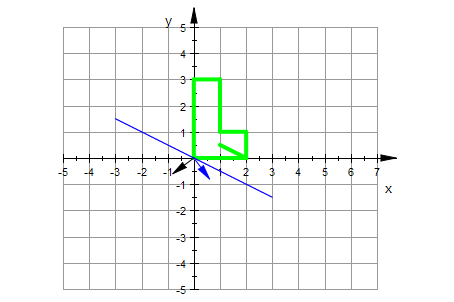
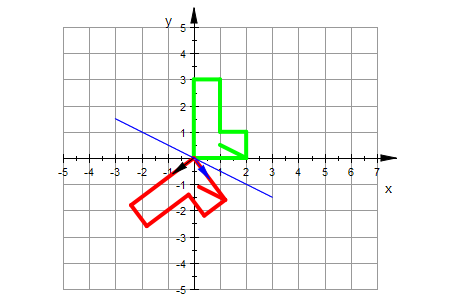
spiegelgerade:=plot::Function2d(m*x,x=-3..3):
urbild:=plot::Polygon2d(myUr,
LineWidth=1, LineColor=RGB::Green, Scaling=Constrained):
e1s:=plot::Arrow2d([0,0],[A[1,1],A[2,1]]):
e2s:=plot::Arrow2d([0,0],[A[1,2],A[2,2]],LineColor=RGB::Black):
transl:=plot::Arrow2d([0,0],trans,LineColor=RGB::Magenta):
plot(urbild,e1s,e2s,transl,spiegelgerade,GridVisible=TRUE, ViewingBox=[-5..7,-5..5])
Transponieren, damit die Spalten die Urbild-Punkte sind:
myUrM:=linalg::transpose(matrix(myUr))

myBM:=A*myUrM +tm(trans) //die Bildpunkte
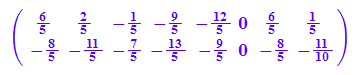
myB:=[[myBM[1,j],myBM[2,j]] $ j=1..npk]:
bild:=plot::Polygon2d(myB,
LineWidth=1, LineColor=RGB::Red):
plot(urbild,bild,e1s,e2s,transl,spiegelgerade,GridVisible=TRUE,
ViewingBox=[-5..7,-5..5])
#######################################################
Dastellung der affinen Verformung
Eh:=matrix([[1,0],[0,1]])
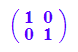
As:=(1-s)*Eh+s*A
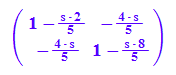
myBMs:=As*myUrM
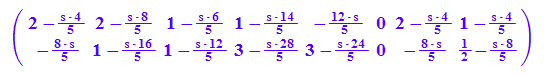
myBs:=[[myBMs[1,j],myBMs[2,j]] $ j=1..npk]:
bilds:=plot::Polygon2d(myBs,s=0..1,
LineWidth=1, LineColor=RGB::Red,
AnimationStyle=BackAndForth):
plot(urbild,bilds,e1s,e2s,spiegelgerade,GridVisible=TRUE,
ViewingBox=[-5..4,-5..3.5])