f:=(p,q,x)->x^3+p*x+q
![]()
Cardanische Formel für Gleichungen 3. Grades
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Okt 04 Update Aug 06
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
f:=(p,q,x)->x^3+p*x+q
![]()
f(2,-1,x)
![]()
plotfunc2d(f(2,-1,x),f(2,-1,x)-x^3,x=-2..2,
ViewingBoxYRange=-5..5)
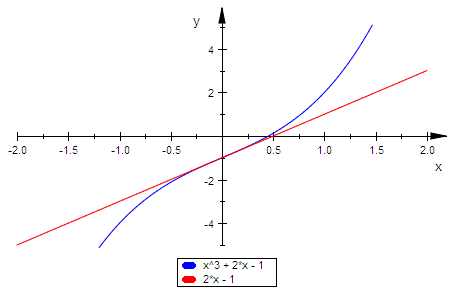
plotfunc2d(f(-7.5,5,x),f(-7.5,5,x)-x^3,x=-4..4)
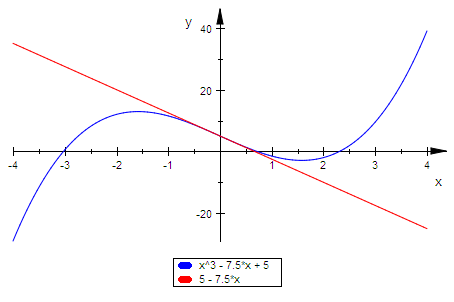
R:=(p,q)->(q/2)^2+(p/3)^3
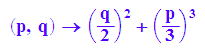
Cardano-Formel
xs:=(-q/2+sqrt(R(p,q)))^(1/3)-(q/2+sqrt(R(p,q)))^(1/3)
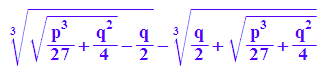
R tritt in der Lösung von Cardano als Radikand einer
Quadratwurzel auf.
Welche Besonderheit entsteht, wenn R=0 ist?
solve(R(p,q)=0,p)
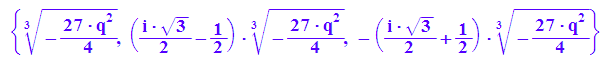
p0:=-3*(q/2)^(2/3)
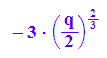
subs(xs,p=p0)
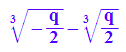
xs0:=-2*(q/2)^(1/3)
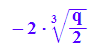
f(p0,q,xs0) //Probe
![]()
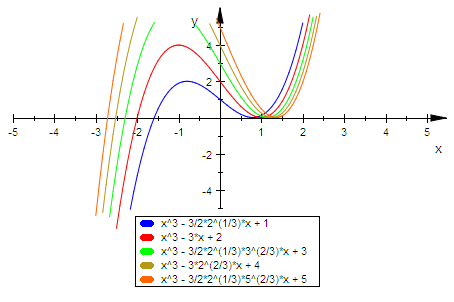
Zugehörige Graphen:
plotfunc2d(f(p0,q,x)$q=1..5,x=-5..5,ViewingBoxYRange=-5..5)
diff(f(p0,q,x),x)
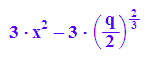
solve(%=0,x)
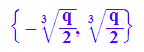
Dieses Ergebnis passt zu den "Affenkastenerkenntnissen"
Man sieht außerdem: weitere Nullstellen können erst entstehen, wenn
bei fest gehaltem q die Wendetangente steiler wird.
plotfunc2d(f(p0-1,q,x)$q=1..5,x=-5..5, ViewingBoxYRange=-5..5)
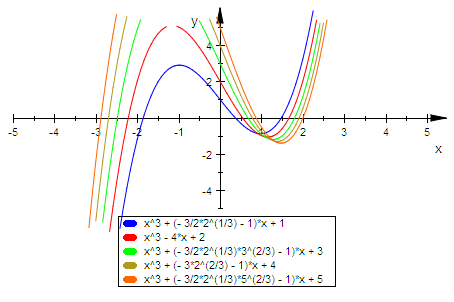
Die Wendetangente hat aber die Steigung p.
plotfunc2d(x^3-7.5*x+5,-7.5*x+5,x=-4..4, ViewingBoxYRange=-5..15)
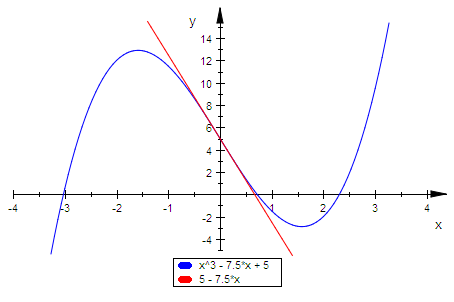
xsk:=subs(subs(xs,p=-7.5),q=5)
![]()
Zu dieser komplexen 3. Wurzel gehören zwei weitere Wurzeln im
Komlexen. Es stellt sich aber heraus, dass eine davon immer reell ist.
Diese hat den gleichen Betrag wie xsk und das Vorzeichen von q.
Also:
xsr:=sign(5)*sqrt(Re(xsk)^2+Im(xsk)^2)
![]()
xs
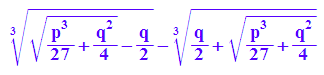
xsreell:=(p,q)->sign(q)*sqrt(Re(xs)^2+Im(xs)^2)
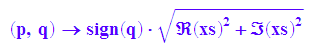
xsr:=float(subs(subs(xsreell(p,q),p=-7.5),q=5))
![]()
Hormerschema ergibt für nachfolgende Parabel:
par:=x->x^2+s*x+s^2+p
![]()
lo:=solve(par(x)=0,x)
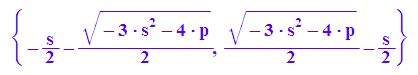
alle:=[op(lo,1),s,op(lo,2)]
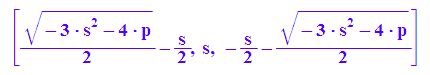
subs(subs(alle,s=xsr),p=-7.5)
![]()
numeric::solve(f(-7.5,5,x)=0,x)
![]()