ukub:=plot::Hexahedron(Radius=1,Center=[0,0,0]);
vkub:=plot::Hexahedron(Radius=1/4,Center=[1.25,1.25,1.25]);
plot(ukub,vkub,platte1,platte2, platte3)
![]()
![]()
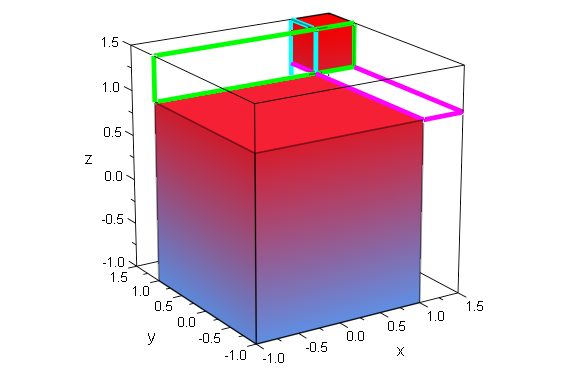
Cardanische Gleichungslösung mit "Würfel"
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Juni 06 Update 23.06.06 repariert Mai 2011
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
platte1:=plot::Polygon3d([[-1,1,1],[-1,1,1.5],[1.5,1,1.5],[1.5,1,1],[-1,1,1]],
LineColor=[0,1,0], LineWidth=1):
platte2:=plot::Polygon3d([[1,1.5,-1],[1,1.5,1.5],[1,1,1.5],[1,1,-1],[1,1.5,-1]],
LineColor=[0,1,1], LineWidth=1):
platte3:=plot::Polygon3d([[1,-1,1],[1,1.5,1],[1.5,1.5,1],[1.5,-1,1],[1,-1,1]],
LineColor=[1,0,1], LineWidth=1):
ukub:=plot::Hexahedron(Radius=1,Center=[0,0,0]);
vkub:=plot::Hexahedron(Radius=1/4,Center=[1.25,1.25,1.25]);
plot(ukub,vkub,platte1,platte2, platte3)
![]()
![]()

3 Platten mit Kante (u+v), Breite u , Höhe v
Großer Würfel (u+v)^3, mittlerer u^3 , kleiner Würfel v^3
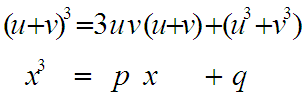
Lösungsvorschlag:
Setze 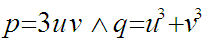
und löse nach u und v auf. Dann ist x=u+v.
hold((u+v)^3)=expand((u+v)^3);
![]()
expand(3*u*v*(u+v))
![]()
Beispiel
##################################
Casus irreduzibilis
gl:= x^3=6*x+1
![]()
solve(gl,x)
![]()
numeric::solve(gl,x)
![]()
solve({6=3*u*v,1=u^3+v^3},{u,v})
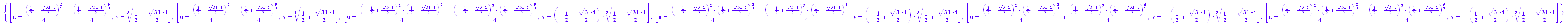
float(%)
![]()
plotfunc2d(x^3,6*x+1,x^3-6*x-1, ViewingBoxYRange=-14..20)
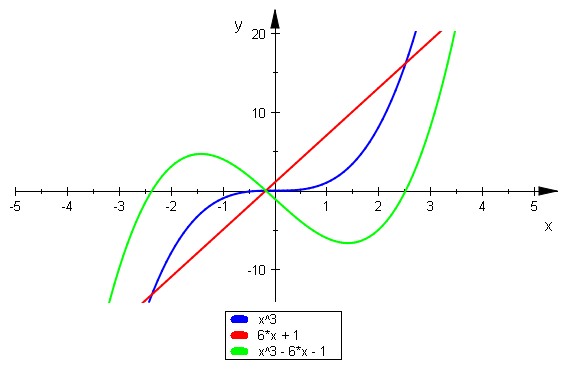
Die Nullstellen der grünen Kurve sind die Schnittstellen von Rot und Blau
Eigene Bearbeitung
ugl:=u^3+(2/u)^3=1
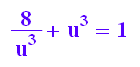
lou:=solve(ugl,u)
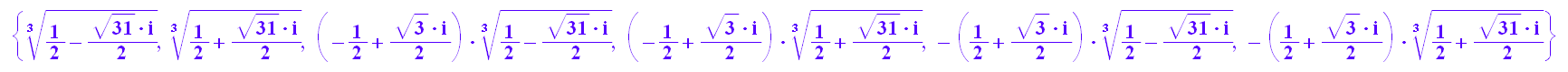
Das sind alle 6 Lösungen, wie man sie auch von Hand findet.
v=p/ (3*u) Hier p=3 , q=1. Hier p/3=2, die 2 unter die Wurzel ergibt 8
8/(1/2 -sqrt(31)/2*I); rectform(%)
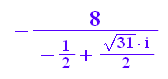
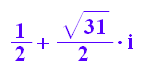
Das sieht man, dass die konjugiert-Komlexen der u^3 die v^3 sind.
Also ist die Lösungsliste gleichzeitig alle 6 u und alle 6 v, immer paarweise.
rectform(lou)
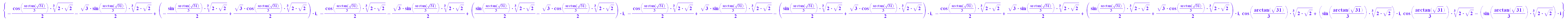
lo:=float(%)
![]()
Die Summen dieser Lösungen sind die Lösungen der gegebenen Gleichung.
(immer zwei konjugiert-komplexe addiert)
lo[1]+lo[2], lo[3]+lo[4], lo[5]+lo[6]
![]()
Re(lo[1]+lo[2]), Re(lo[3]+lo[4]), Re(lo[5]+lo[6])
![]()
numeric::solve(gl,x)
![]()
Beispiel 2
##################################
Casus irreduzibilis
gl:= x^3=3*x-1
![]()
solve(gl,x)
![]()
numeric::solve(gl,x)
![]()
solve({3=3*u*v,-1=u^3+v^3},{u,v})
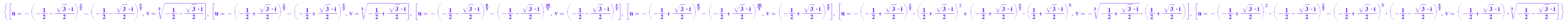
Mir ist nicht klar, wie MuPAD auf diese Darstellung kommt.
u1:=rectform( - (- 1/2 - 3^(1/2)*1/2*I)^(2/3) - (- 1/2 - 3^(1/2)*1/2*I)^(5/3))
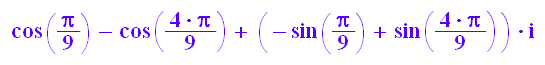
v1:=rectform((-1/2-sqrt(3)/2*I)^(1/3))
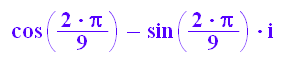
float(u1+v1)
![]()
float(%)
![]()
plotfunc2d(x^3,3*x-1,x^3-3*x+1, ViewingBoxYRange=-8..5, GridVisible=TRUE)
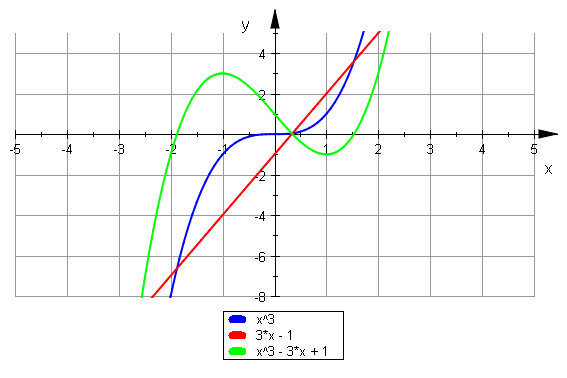
(p/(3 u))^3+u^3 =q oder ebenso für v
ugl:=u^3+(1/u)^3=-1
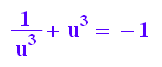
solve(ugl,u)
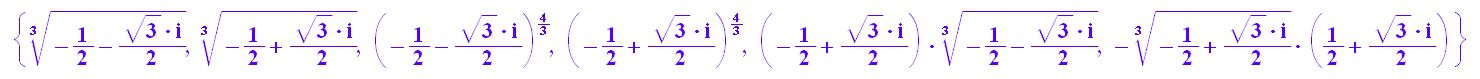
lo:=float(%)
![]()
Die u-Liste und die v-Liste sind identisch ( s.o.)
Die Summen dieser Lösungen sind die Lösungen der gegebenen Gleichung.
(immer zwei konjugiert-komplexe addiert)
lo[1]+lo[2], lo[3]+lo[4], lo[5]+lo[6]
![]()
Re(lo[1]+lo[2]), Re(lo[3]+lo[4]), Re(lo[5]+lo[6])
![]()
numeric::solve(gl,x)
![]()
###################################################
Beispiel 3 mit genau einer reellen Nullstelle
gl:= x^3=1/2*x+1/5
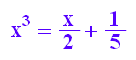
solve(gl,x)
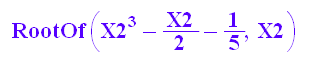
numeric::solve(gl,x)
![]()
solve({1/2=3*u*v,1/5=u^3+v^3},{u,v})
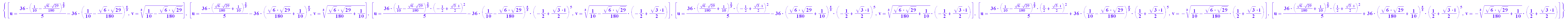
float(%)
![]()
plotfunc2d(x^3,1/2*x+1/5,x^3-1/2*x-1/5, x=-2..2,
ViewingBoxYRange=-0.5..0.75, GridVisible=TRUE)
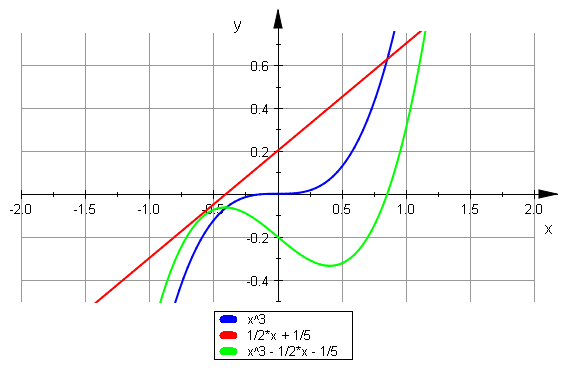
Die Nullstellen der grünen Kurve sind die Schnittstellen von Rot und Blau
Jeweils gibt es genau eine Stelle.
Eigene Bearbeitung
ugl:=u^3+(1/(6*u))^3=1/5
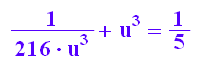
lou:=solve(ugl,u)
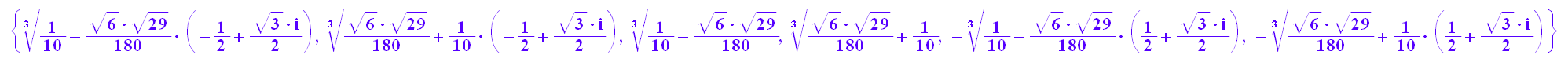
Das sind alle 6 Lösungen, wie man sie auch von Hand findet.
v=p/ (3*u) Hier p=1/2 , q=1/5. Hier p/3=1/6, die 1/6 unter die Wurzel ergibt 1/216
1/216*1/(1/10 -sqrt(6*29)/180); rectform(%)
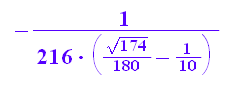
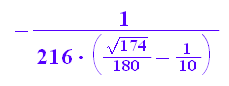
Das sieht man, dass die konjugiert-Komlexen der u^3 die v^3 sind.
Also ist die Lösungsliste gleichzeitig alle 6 u und alle 6 v, immer paarweise.
rectform(lou)
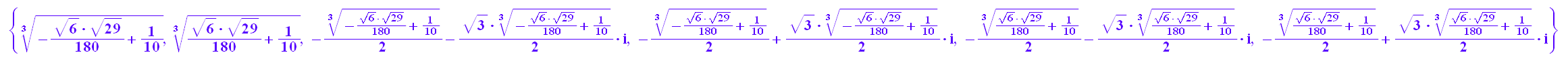
lo:=float(%)
![]()
Die Summen dieser Lösungen sind die Lösungen der gegebenen Gleichung.
(immer zwei konjugiert-komplexe addiert) Hier gibt das Problem, dass die Liste
immer konjugiert-Komplexe hintereinander auflistet, aber die sind nicht zusammenpassende
u und v.
lo[1]+lo[2], lo[3]+lo[6], lo[4]+lo[5]
![]()
Es musste also anders kombiniert werden. Es falsch, nur die Realteile zu nehmen.
Re(lo[1]+lo[2]), Re(lo[3]+lo[4]), Re(lo[5]+lo[6])
![]()
numeric::solve(gl,x)
![]()
Prüfung der Gleichung p=3 u v
lo[3]*lo[6]-1/6;
lo[4]*lo[5]-1/6
![]()
![]()
ok, aber für die konjugiert-Komlexen ist dies nicht wahr.
lo[3]*lo[4]-1/6;
lo[5]*lo[6]-1/6
![]()
![]()
########################################
Nebenrechnung von Hand, geht ganz ohne komplexe Zahlen.
w1:=1/10+sqrt(1/100-1/6^3);w2:=1/10-sqrt(1/100-1/6^3);
float(w1); float(w2);
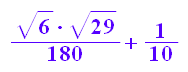
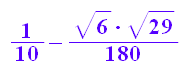
![]()
![]()
u1:=w1^(1/3); u2:=w2^(1/3);
float(u1); float(u2);
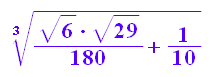
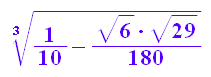
![]()
![]()
v1:=1/6/u1; v2:=1/6/u2;float(v1); float(v2);
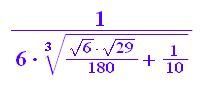
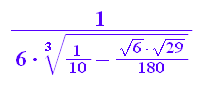
![]()
![]()
u1+v1,u2+v2
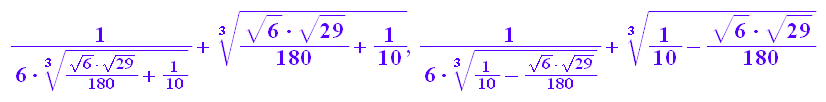
float(u1+v1); float(u2+v2)
![]()
![]()
1/100-116/21600
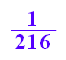
116/21600

(1/10-sqrt(116/21600))^(1/3);float(%);
(1/10+sqrt(116/21600))^(1/3);float(%);
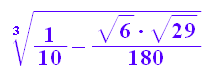
![]()
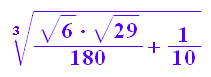
![]()
passt
![]()