
| Nr. | Name | Definition | Algebra |
|---|---|---|---|
| 1 | Punkt O | O = (0, 0) | |
| 2 | Zahl p | p = 10 | |
| 3 | Punkt P | (p, 0) | P = (10, 0) |
| 4 | Punkt C | Mittelpunkt von (0, 0), P | C = (5, 0) |
| 5 | Kreis f | Kreis mit Mittelpunkt C durch O | f: (x - 5)² + y² = 25 |
| 6 | Zahl q | q = 64 | |
| 7 | Zahl q' | sqrt(q) | q' = 8 |
| 8 | Punkt A | (0, q') | A = (0, 8) |
| 9 | Gerade h | Gerade durch A, C | h: 8x + 5y = 40 |
| 10 | Punkt M | Schnittpunkt von f, h | M = (2.35001, 4.23999) |
| 10 | Punkt N | Schnittpunkt von f, h | N = (7.64999, -4.23999) |
| 11 | Kreis d | Kreis mit Mittelpunkt C durch A | d: (x - 5)² + y² = 89 |
| 12 | Strecke z | Strecke[A, C] | z = 9.43398 |
| 13 | Gerade i | Gerade durch M senkrecht zu z | i: 5x - 8y = -22.16991 |
| 14 | Gerade c | Gerade durch C senkrecht zu z | c: 5x - 8y = 25 |
| 15 | Punkt K | Schnittpunkt von f, c | K = (9.23999, 2.64999) |
| 15 | Punkt L | Schnittpunkt von f, c | L = (0.76001, -2.64999) |
| 16 | Punkt D | Schnittpunkt von d, c | D = (13, 5) |
| 16 | Punkt E | Schnittpunkt von d, c | E = (-3, -5) |
| 17 | Gerade b | Gerade durch A senkrecht zu z | b: 5x - 8y = -64 |
| 18 | Kreis e | Kreis mit Mittelpunkt A durch C | e: x² + (y - 8)² = 89 |
| 19 | Strecke p' | Strecke[O, C] | p' = 5 |
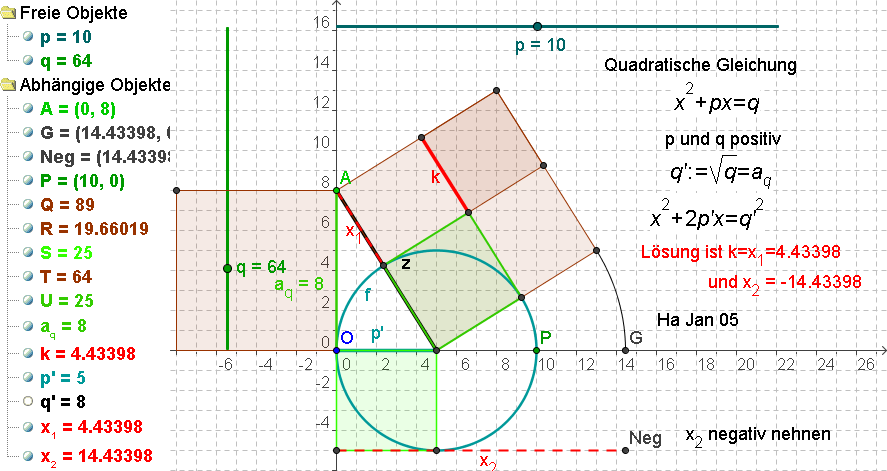
| 20 | Text T1 | T1 = "Quadratische Gleichung" | |
| 21 | Text T3 | T3 = "x^2+p x=q" | |
| 22 | Text T2 | T2 = "x^2+2 p' x=q'^{ 2}" | |
| 23 | Text T6 | T6 = "Ha Jan 05" | |
| 24 | Text T7 | T7 = "p und q positiv" | |
| 25 | Punkt A1 | (-q', q') | A1 = (-8, 8) |
| 26 | Punkt A2 | (-q', 0) | A2 = (-8, 0) |
| 27 | Punkt C1 | (0, -p / 2) | C1 = (0, -5) |
| 28 | Punkt C2 | (p / 2, -p / 2) | C2 = (5, -5) |
| 29 | Vieleck S | Vieleck O, C1, C2, C | S = 25 |
| 29 | Strecke o | Strecke[O, C1] von Vieleck S | o = 5 |
| 29 | Strecke c1 | Strecke[C1, C2] von Vieleck S | c1 = 5 |
| 29 | Strecke c2 | Strecke[C2, C] von Vieleck S | c2 = 5 |
| 29 | Strecke c2 | Strecke[C, O] von Vieleck S | c2 = 5 |
| 30 | Vieleck T | Vieleck O, A, A1, A2 | T = 64 |
| 30 | Strecke aq | Strecke[O, A] von Vieleck T | aq = 8 |
| 30 | Strecke a0 | Strecke[A, A1] von Vieleck T | a0 = 8 |
| 30 | Strecke a1 | Strecke[A1, A2] von Vieleck T | a1 = 8 |
| 30 | Strecke a2 | Strecke[A2, O] von Vieleck T | a2 = 8 |
| 31 | Punkt B | Schnittpunkt von e, b | B = (-8, 3) |
| 31 | Punkt F | Schnittpunkt von e, b | F = (8, 13) |
| 32 | Vieleck Q | Vieleck A, C, D, F | Q = 89 |
| 32 | Strecke a1 | Strecke[A, C] von Vieleck Q | a1 = 9.43398 |
| 32 | Strecke c1 | Strecke[C, D] von Vieleck Q | c1 = 9.43398 |
| 32 | Strecke d1 | Strecke[D, F] von Vieleck Q | d1 = 9.43398 |
| 32 | Strecke f1 | Strecke[F, A] von Vieleck Q | f1 = 9.43398 |
| 33 | Gerade g | Gerade durch K senkrecht zu c1 | g: 8x + 5y = 87.16991 |
| 34 | Punkt J | Schnittpunkt von g, i | J = (6.59, 6.88999) |
| 35 | Punkt H | Schnittpunkt von g, b | H = (4.23999, 10.64999) |
| 36 | Punkt I | Schnittpunkt von d1, i | I = (10.35001, 9.23999) |
| 37 | Vieleck R | Vieleck H, J, I, F | R = 19.66019 |
| 37 | Strecke k | Strecke[H, J] von Vieleck R | k = 4.43398 |
| 37 | Strecke j | Strecke[J, I] von Vieleck R | j = 4.43398 |
| 37 | Strecke i1 | Strecke[I, F] von Vieleck R | i1 = 4.43398 |
| 37 | Strecke f2 | Strecke[F, H] von Vieleck R | f2 = 4.43398 |
| 38 | Text T8 | T8 = "q':=\sqrt {q}=aq" | |
| 39 | Strecke x1 | Strecke[A, M] | x1 = 4.43398 |
| 40 | Vieleck U | Vieleck M, J, K, C | U = 25 |
| 40 | Strecke m | Strecke[M, J] von Vieleck U | m = 5 |
| 40 | Strecke j1 | Strecke[J, K] von Vieleck U | j1 = 5 |
| 40 | Strecke k1 | Strecke[K, C] von Vieleck U | k1 = 5 |
| 40 | Strecke c3 | Strecke[C, M] von Vieleck U | c3 = 5 |
| 41 | Kreis r | Kreis mit Mittelpunkt C durch D | r: (x - 5)² + y² = 89 |
| 42 | Punkt G | Schnittpunkt von r, xAchse | G = (14.43398, 0) |
| 43 | Punkt Neg | (x(G), -p') | Neg = (14.43398, -5) |
| 44 | Strecke x2 | Strecke[C1, Neg] | x2 = 14.43398 |
| 45 | Bogen s | Kreisbogen[C, G, D] | s = 5.26982 |
| 46 | Text T5 | T5 = "x2 negativ nehnen" | |
| 47 | Text T4 | "Lösung ist k=x1=" + k | T4 = "Lösung ist k=x1=4.43398" |
| 48 | Text T9 | "und x2 = " + (-x(G)) | T9 = "und x2 = -14.43398" |