Lineare Algebra

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Dez 2010

0.1 Handling

Achtung: Durch Anklicken der linken Zellmarkierung kann man die
Abschnitte und auch einzelne Zellen aufklappen und auch wieder zuklappen.

Endung *.wxmx ist komfortabel. Ist die Endung *.wxm muss man
erst noch alle Ausgaben neu erzeugen. Mit Strg r werden alle aufgeklappten Zellen ausgewertet.
Zum Lernen ist es besser die Zellen einzeln (mit Shift+Enter) auszuwerten.

Werte einzelne Zellen aus mit Shift-Enter.
Auswertung in einem Rutsch: Falte alle Abschnitte auf,
werte alle Zellen mit Strg r aus ( auch Menu Cell Alle Zellen auswerten).

wxMaxima ist über Maxima und Macsyma ein Lisp-Abkömmling.
Die Sprache Lisp ist Listenorientiert. Daher spielt auch bei
wxMaxima das Listenkonzept eine große Rolle.

0.2 Inhalt

1 Matrizen und Vektoren
    1.1 Definition von Matrizen
    1.2 Verändern von Matrizen
    1.3 Rechnen mit Matrizen
2 Lineare Gleichungssysteme
    2.1 Betrachung der Koeffizientenmatrix
    2.2 Gleichungen, bei denen die Varablen genannt werden
    2.3 Gleichungen, bei deren Lösung Variable belegt werden
    2.4 Lineare Gleichungen mit Matrizen lösen
    2.5 Automatisches Aufstellen des Gleichungssystems
3 Affine Abbildungen

1 Matrizen und Vektoren

1.1 Definition von Matrizen

Direkte Eingabe zeilenweise in Listen:

(%i1) cc:matrix([1,2,3,4],[5,6,7,8],[x,b,c,d]);
bb:matrix([8,9],[-1,2],[3,-4]);

der Doppelpunkt ist in Maxima das Zuweisungszeichen

Interaktive Eingabe,
Achtung: nach jeder Zeile shift+Enter
Erst /* und */1 löschen, eigefügt,
damit automatische Auswertung klappt

(%i108) /* aa:entermatrix(2,3) */1;

(%i107) aa:matrix([9,6,-6],[-3,-9,4]);

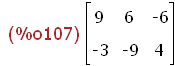
Wenn man sich bei dieser Methode verschrieben hat, markiert man die Ausgabe,
kopiert sie mit strg c

1.2 Verändern von Matrizen

Anfügen einer Zeile

(%i5) aaa:addrow(aa,[0,-7,8]);

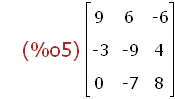
(%i6) bv:transpose(matrix([9,-2,7]));

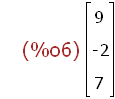
transpose sorgt für die Spaltenform

(%i7) aae:addcol(aaa,[9,-2,7]);

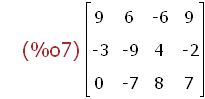
Mit addcol kann man aber auch eine einfache Liste als
Spalte anfügen, bv hätte man auch schreiben können statt [9,-2,7].

So erhält man also die erweiterte Matrix

1.3 Rechnen mit Matrizen

(%i8) aaa.bb;

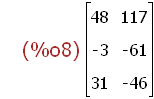
Achtung, Multiplikation mit Punkt statt mit dem mal-*

Transponieren einer Matrix

(%i9) bbt:transpose(bb);

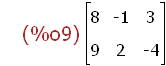
(%i10) aa+5*aa;

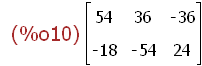
Anfügen einer Zeile

(%i11) bbb:addrow(bbt,[1,-2,-3]);

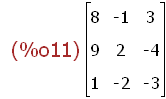
Addition, Subtraktion

(%i12) [aaa+bbb,aaa-bbb];

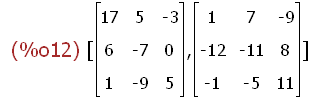
Wie erwartet komponentenweise, in einer Zeile notiert zum Platzsparen.

2 Gleichungssysteme

2.1 Betrachtung der Koeffizienzenmatix

Beispiel das auch am TI Nspire vewendet ist

Fassen wir aae als lineares Gleichungssystem auf.
Drei Variabe, drei Gleichungen mit rechter Seite.

(%i13) aae;

(%i14) triangularize(aae);

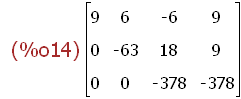
(%i15) echelon(aae);

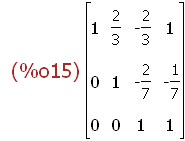
Dieser Befehl entspricht ref(M) beim TI Nspire.

(%i16) rank(aae);

Dieses kann man dann entsprechend deuten.

2.2 Gleichungen, bei denen die Varablen genannt werden

(%i20) g1:9*r+6*s-6*t=9;
g2:-3*r-9*s+4*t=-2;
g3:-7*s+8*t=7;

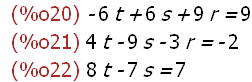
Den nachfolgenden Eintrag erhält man interaktiv mit dem Menü
Gleichunegen->löse lineares System. Man trägt dann g1, g2 und g3 ein,
bei Variablen trägt man r,s,t ein, mit Kommata getrennt.

(%i23) linsolve([g1, g2, g3], [r,s,t]);

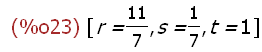
(%i24) linsolve([g1,g2,g3],[r,s,t]);

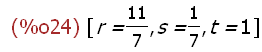
(%i25) [r,s,t];

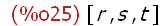
Hier werden die Ergebnisse nur angezeigt.

2.3 Gleichungen, bei deren Lösung Variable belegt werden

(%i26) globalsolve:true$

(%i27) linsolve([g1,g2,g3],[r,s,t]);

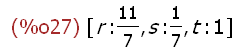
(%i28) [r,s,t];

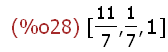
Nun sind r,s und t belegt und nicht mehr frei.

(%i29) [g1, g2,g3];

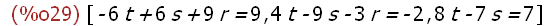
(%i30) linsolve([g1,g2,g3],[r,s,t]);

Man kann das Gls nicht mehr lösen.
Darum stelle ich leber wieder die Globale Option zurück auf den
voreingestellten Wert false

(%i31) globalsolve:false$

(%i48) remvalue(r,s,t)$ [r,s,t];

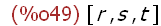
Die Variablen sollen wieder freigegeben werden

2.4 Lineare Gleichungen mit Matrizen lösen

(%i32) xv:transpose(matrix([xx,yy,zz]));

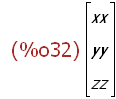
(%i33) aaa;

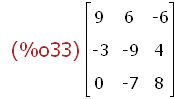
Wenn die Koeefizientenmatrix ein Inverses hat,
dann ist die Lösung ds Sytem aaa.xv=bv zu haben:

(%i34) ainv:invert(aaa);

(%i35) xv=ainv.bv;

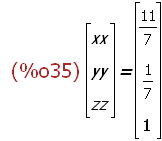
(%i36) xv[1,1];

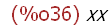
Hier finden keine Zuweisungen statt

2.5 Automatisches Aufstellen des Gleichungssystems

(%i60) angl:3 /*Anzahl der Glaichungen*/$

(%i61) glsli:makelist((aaa.xv) [i,1]=bv[i,1],i,1,angl);

(%i62) linsolve(glsli,[xx,yy,zz]);

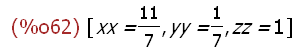
(%i63) solve(glsli,[xx,yy,zz]);

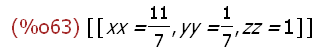
3 Affine Abbildungen, rechnerisch

(%i100) aaa;

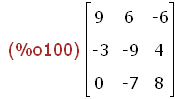
(%i101) tx:1$ ty:2$ tz:-1$

(%i104) tv:transpose(matrix([tx,ty,tz]));

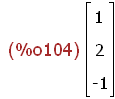
(%i105) f(xv):=aaa.xv+tv;

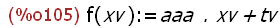
(%i96) f(xv);

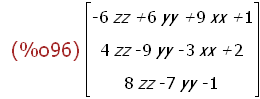
(%i72) aaa.aaa;

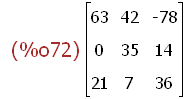
(%i71) aaa;

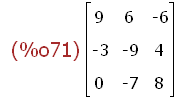
(%i97) tvm(tv):=addcol(tv,tv,tv);

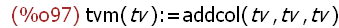
(%i98) fm(xv):=aaa.xv+tvm(tv);

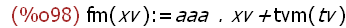
(%i99) fm(aaa);