o:=matrix([0,0,0]):
a:=matrix([4,2,-1]):
v:=matrix([3,1,-4]):
w:=matrix([2,3,-5]): a,v,w
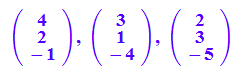
Skalarprodukt, Hessesche Normalform
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4.0, ( MuPAD 3 im Okt. 05) Update 8.06.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
o:=matrix([0,0,0]):
a:=matrix([4,2,-1]):
v:=matrix([3,1,-4]):
w:=matrix([2,3,-5]): a,v,w
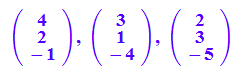
Ebene
ebene:=a+ r*v+s*w
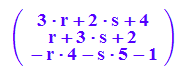
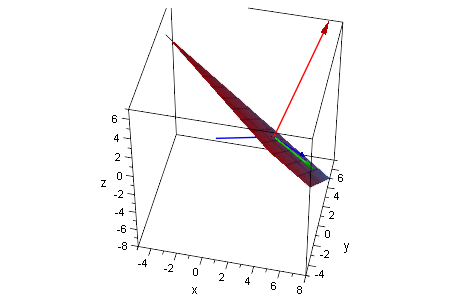
apkt:=plot::Point3d(a):
av:=plot::Arrow3d(o,a):
vv:=plot::Arrow3d(a,a+v, LineColor=[0,1,0]):
ww:=plot::Arrow3d(a,a+w):
eb:=plot::Surface(ebene,r=-5..5,s=-5..5,
ViewingBox=[-5..8,-5..6,-8..5]):
plot(eb,apkt,ww,vv,av, Scaling=Constrained)
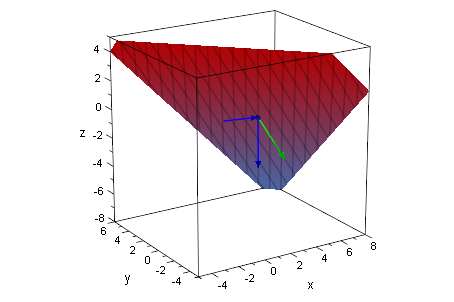
Skalarprodukt
vw:=linalg::scalarProduct(v,w);
lvq:=linalg::scalarProduct(v,v);
lwq:=linalg::scalarProduct(w,w);
![]()
![]()
![]()
Berechnung der Winkels zwischen v und w
cosi:=vw/sqrt(lvq*lwq); float(cosi);
float(arccos(cosi)*180/PI)
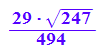
![]()
![]()
Das ist der Winkel im Gradmaß
-----------------------------------------------------
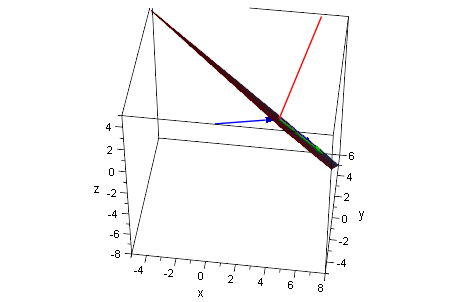
Kreuzprodukt
n:=linalg::crossProduct(v,w);
nv:=plot::Arrow3d(a,n, LineColor=[1,0,0]):
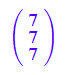
plot(eb,nv,av,vv,ww,Scaling=Constrained)
Hessesche Normalenform
p:=matrix([x,y,z]):
ehess:=(linalg::scalarProduct((p-a),n)=0)
![]()
eh:=plot::Implicit3d(ehess,x=-5..8,y=-5..5,z=-8..5):
plot(eh,av,nv,vv,ww, Scaling=Constrained)