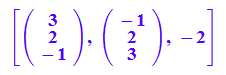a := matrix([3,2]);
v := matrix([6,-2]);
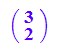
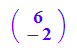
Vektoren, Geraden ,Ebenen
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Mrz 06 Update 14.03.06
Es fehlen nocht textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1. Vektoren 2D #######
2. Vektoren 3D #######
3. Zwei Geraden #######
4. Ebenen #######
5. Geraden und Ebenen #######
6. Mehrere Ebenen #######
7. Skalarprodukt, Hessesche Normalform....--> Extraseite
1.Vektoren 2D ###################################
Vektoren werden als Matrizen aufgefasst.
Eingabe einer "flachen" Liste erzeugt Spaltenvektoren.
a := matrix([3,2]);
v := matrix([6,-2]);
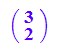
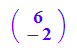
Definition eines Zeilenvektors mit Doppelliste:
az := matrix([[3,2]]);
![]()
Hier wird eine Gerade als Funktion ihres Parameters definiert.
Es ginge aber auch als Term g:=a+r*v
gv:=r->a+r*v
![]()
gv(r)
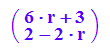
p1:=gv(1)
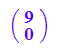
Zum Zeichnen nimmt man den Pfeil-Befehl.
Es werden drei Graphik-Primitive erzeugt, die dann von plot dargestellt werden.
ag:=plot::Arrow2d(a);
p1g:=plot::Arrow2d(a+v);
vg:=plot::Arrow2d(a,a+v);
![]()
![]()
![]()
plot(ag,vg,p1g)
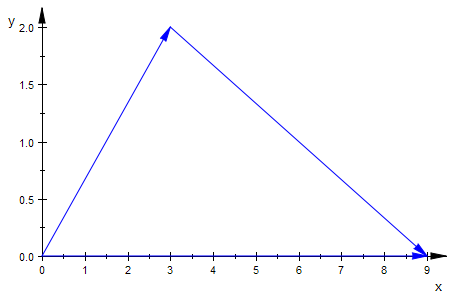
Eindrucksvolle annimierte Geradendarstellung:
vani:=plot::Arrow2d(a,gv(r),r=-2..2)
![]()
plot(ag,vani)
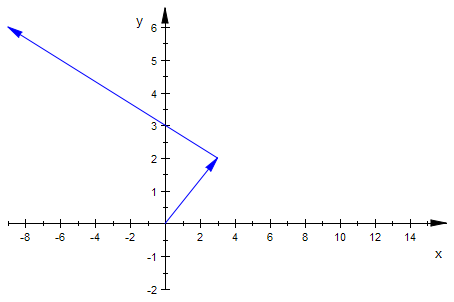
Zum Animieren: Doppeklick in der Graphik, dann oben Player bedienen.
Herausgreifen der Zeilen aus den Verktoren:
gv(r)[1]
![]()
Herstellen der üblichen 2d-Geradengleichung
gr:=solve({gv(r)[1]=x,gv(r)[2]=y},{y,r})
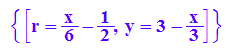
Hinten kann mann die Gleichung ablesen.
Automatisches Herausgreifen:
gerade:=gr[1][2][2]
![]()
geradeg:=plot::Function2d(gerade,x=-10..16, LineColor=RGB::Red):
plot(geradeg,ag,vani);
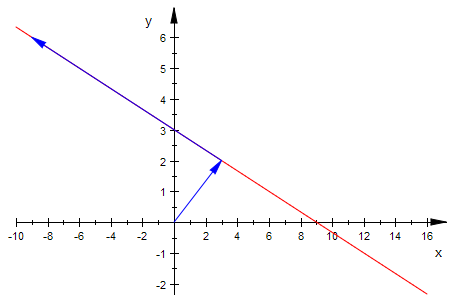
Zum Animieren: Doppeklick in der Graphik, dann oben Player bedienen.
2.Vektoren 3D ##########################################
Vektoren werden als Matrizen aufgefasst.
Eingabe einer "flachen" Liste erzeugt Spaltenvektoren.
a := matrix([3,2,-1]);
v := matrix([6,-2,2]); o:=matrix([0,0,0]):
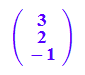
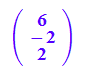
Hier wird eine Gerade als Funktion ihres Parameters definiert.
Es ginge aber auch als Term g:=a+r*v
gv:=r->a+r*v
![]()
gv(r); gv(1)
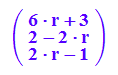
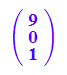
Zum Zeichnen nimmt man den Pfeil-Befehl.
Es werden drei Graphik-Primitive erzeugt, die dann von plot dargestellt werden
ag:=plot::Arrow3d(a);
p1g:=plot::Arrow3d(a+v);
vag:=plot::Arrow3d(a,a+v);
![]()
![]()
![]()
plot(ag,vag,p1g)
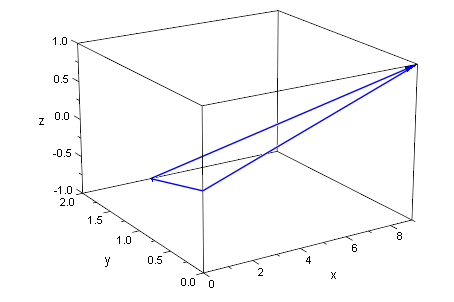
3D-Graphik "anfassen", d.h. Doppelkick in der Graphik, dann mit Maus drehen.
Verändern der Eigenschaften:
ag::LineColor:=RGB::Green:
vag::LineColor:=RGB::Magenta:
p1g::LineStyle:=Dashed:
plot(ag,vag,p1g, Axes=Origin)
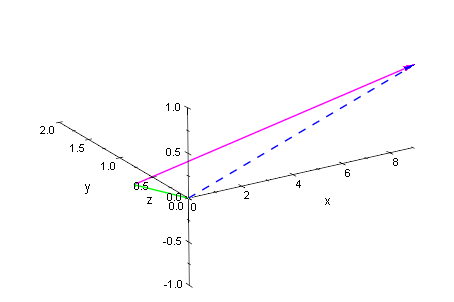
Funktion, die 3 Vektoren in eine Liste umwandelt
vek3Liste:=(v1,v2,v3)->[[ v1[i]$i=1..3 ],[ v2[i]$i=1..3 ],[ v3[i]$i=1..3] ]:
vek3Liste(o,a,a+v)
![]()
3d-Polygone können genau dann gefüllt werden, wenn es sich um Dreiecke handelt.
dreieck:=plot::Polygon3d(vek3Liste(o,a,a+v),Filled=TRUE)
![]()
plot(dreieck,ag,vag,p1g, Axes=Origin)
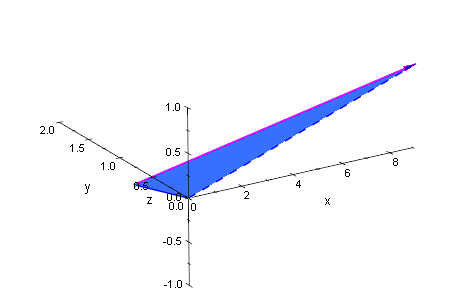
Beim Drehen der Graphik kann man nun schön die räumliche Anordnung sehen.
3. Zwei Geraden ####################################
w:=matrix([1,1,3]);
wag:=plot::Arrow3d(a,a+w, LineColor=RGB::Black);
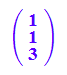
![]()
b:=2*a;
bg:=plot::Arrow3d(b)
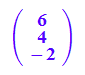
![]()
gw:=r->b+r*w
![]()
solve(gw(r)=gv(s),{r,s})
![]()
Das überrascht nicht. Die Geraden sind windschief.
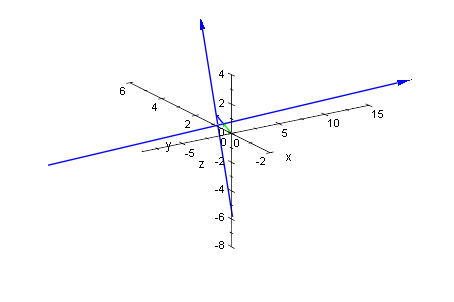
Zeichnen von Geraden im Raum
Die einfachste Art ist, den Orts- und den Richtungsvektor (oder ein Vielfaches) zu zeichnen
gvg:=plot::Arrow3d(a-2*v,a+2*v):
gwg:=plot::Arrow3d(b-2*w,b+2*w):
plot(ag,gvg,bg,gwg, Axes=Origin)
4. Ebenen #######################################
Nun soll eine Ebene definiert werden, diesmal ohne Funktion.
eb:=a+r*v+s*w:
[a,v,w,eb];
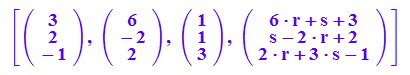
Die Angabe als Liste ist eine Lesehilfe.
plot(ag,vag,wag)
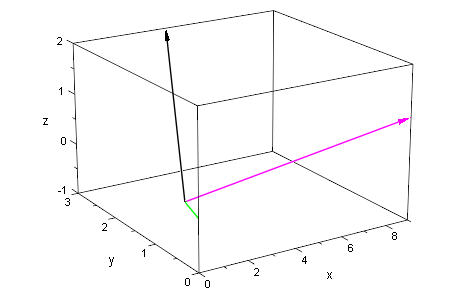
Bessere Sicht mit Ebenendreieck
ebene:=plot::Polygon3d(vek3Liste(a,a+v,a+w),Filled=TRUE);
![]()
[a,v,w]
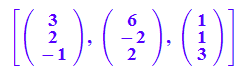
[a,a+v,a+w]
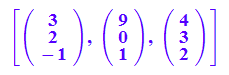
ag;vag;wag;
![]()
![]()
![]()
plot(ebene,ag,vag,wag)
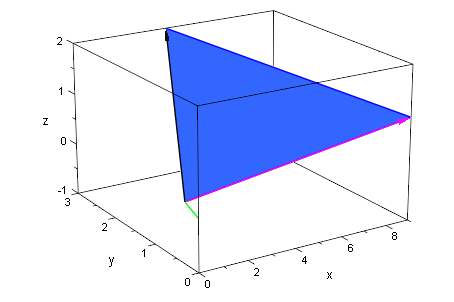
5. Gerade und Ebene
c:=matrix([-1,2,3]);
cg:=plot::Arrow3d(c);
u:=matrix([8,0,-4]);
ucg:=plot::Arrow3d(c,c+u,LineColor=RGB::Red);
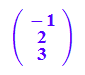
![]()

![]()
plot(cg,ucg,ebene,ag,vag,wag)
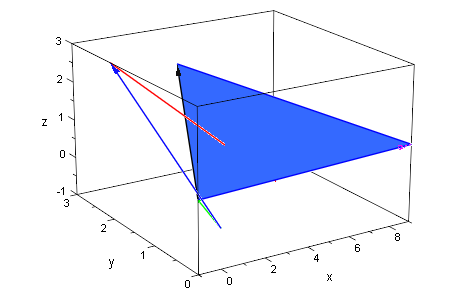
gu:=r->c+r*u;
![]()
eb=gu(t)
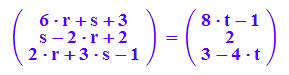
solve(eb=gu(t),{r,s,t})
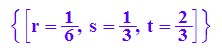
Die Ebene und die Gerade schneiden sich.
Probe und Schnittpunkt
[subs(eb, r=1/6, s= 1/3), gu(2/3)]
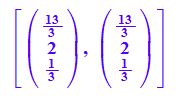
6. Mehrere Ebenen ###########################
ebe:=(r,s)->c+r*u+s*(v+w): [c,u,v+w]; ebe
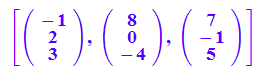
![]()
ebeg:=plot::Polygon3d(vek3Liste(c,c+u,c+(v+w)),
Filled=TRUE, FillColor=[1,0.5,0.5]);plot(ebeg)
![]()
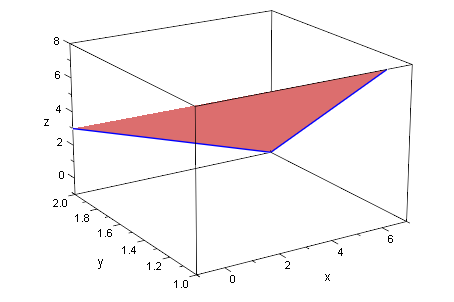
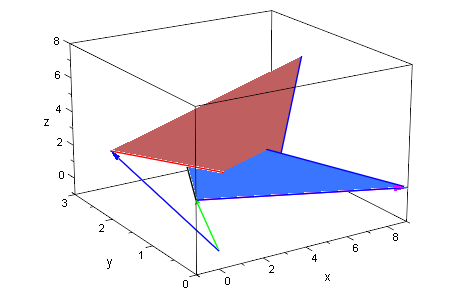
plot(cg,ucg,ebeg,ag,vag,wag,ebene)
eb=ebe(t,k)
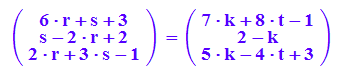
solve(eb=ebe(t,k),{t,k,r})
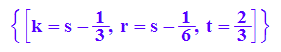
Bei drei Gleichungen für die 4 Parameter ist zu erwarten,
dass i.a. ein Parameter unbestimmt bleibt. Hier ist es das s.
Man kann also ablesen, dass Die folgende Gerade Schnittgerade ist:
Übrigens hier zeigt sich, dass es günstig ist, Geraden und Ebenen als Funktionen
ihrer Parameter aufzufassen.
gs:=s->ebe(2/3,s-1/3);
gsg:=plot::Arrow3d(gs(0),gs(1))
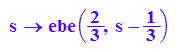
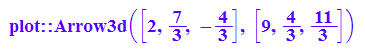
plot(cg,ucg,ebeg,ag,vag,wag,ebene,gsg)
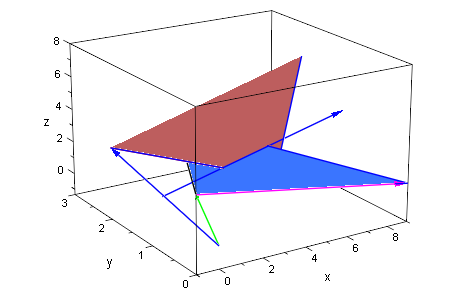
Orts und Richtungsvektor der Schnittgeraden sind:
Oben ist nur der Richtungsvektor passend eingezeichnet.
[gs(0),gs(1)-gs(0)]

7. Skalarprodukt, Hessesche Normalform.... --> Extraseite
[a,c,a.c]
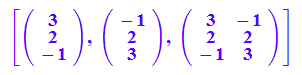
_plus(x[i]*y[i] $i=1..3);
![]()
skalar3:=(x,y)-> _plus(x[i]*y[i] $i=1..3):
[a,c,skalar3(a,c)]