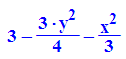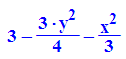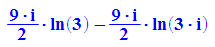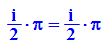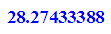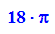Elliptisches Paraboloid
Prof. Dr. Dörte Haftendorn Mathematik Mit MuPAD 3 Juli 05
####################################################
Schritt 1
Aufstellung der Gleichung eines parbolischen Hutes,
der in der x-y-Ebene als Schnitt eine Ellipse mit den Halbachsen2 und 3 hat,
und bis zur Höhe 3 reicht. (Mittelpunktslage)

• f:=(x,y)->3-1/3*x^2-3/4*y^2:
  f(x,y)

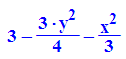
Zeichnung dazu

• plotfunc3d(f(x,y))

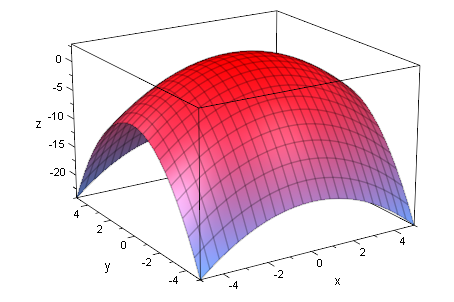
Nur von -3 bis +3 mit Koordinatenebene

• plotfunc3d(f(x,y),0,x=-3..3,y=-3..3)

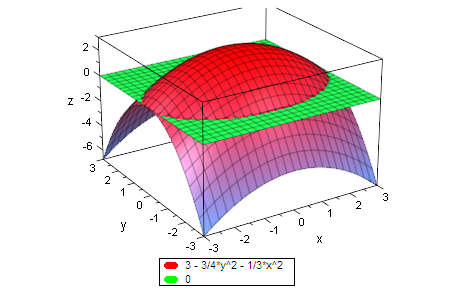
Doppelt anklicken und mit den Maustasten bewegen.
##############################################
Schritt 2
Bestimmung des Volumens
Erstmal reicht es, 1/4-Hut zu berechnen.
Die Integration über y muss dann von der x-Achse bis zum Ellipsenrand gehen.
Die Integration über x muss danach von der y-Achse bis 3 gehen.

• int(f(x,y), y)

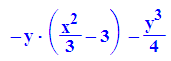
• expl:=solve(x^2/9+y^2/4=1,y)

• rand:=op(expl,1)

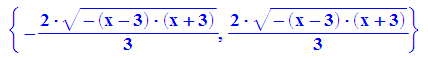
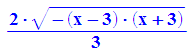
• innen:=int(f(x,y), y=0..rand)

• innen:=simplify(innen)

• assume(x,Type::Real) 

• int(innen,x)

• int(innen,x=0..3)

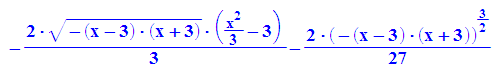
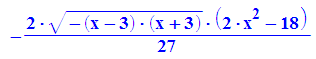
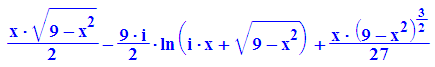
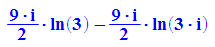
Es gilt

• ln(I)=PI/2*I

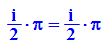
Damit folgt oben

• V:=4*(9/2)*(I*ln(3)-I*ln(3)-I*PI/2*I)

• float(%)

##########################################
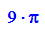
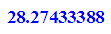
Schritt 3
Vergleichskörper Elliptischer Zylinder

• VZ:=PI*2*3*3

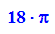
Vergleichskörper elliptischer Kegel

• VK:=PI*2*3*3/3

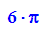
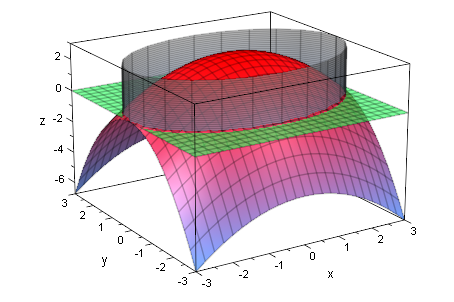
• ph:=plot::Function3d(f(x,y),x=-3..3,y=-3..3):
  pe:=plot::Function3d(0,x=-3..3,y=-3..3):
  pz:=plot::Surface([3*cos(t),2*sin(t),z],t=0..2*PI,z=0..3):
  plot(ph,pe,pz)
  
  
  

• pi:=plot::Implicit3d(f(x,y)-z 
  ,
                        x = -3..3,
                        y = -2..2,
                        z = 0..3,
       Scaling = Constrained)

• plot(pi,pz,pe)

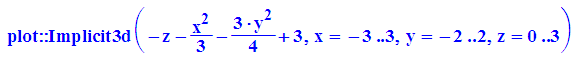
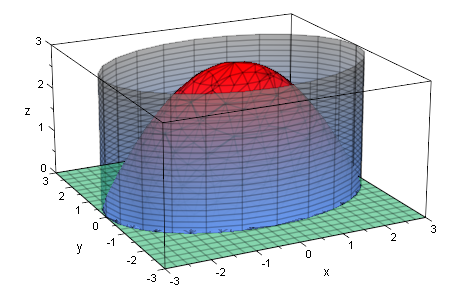
Fazit: Das elliptische Paraboloid nimmt die
Hälfte des entsprechenden elliptischen Zylinders ein.