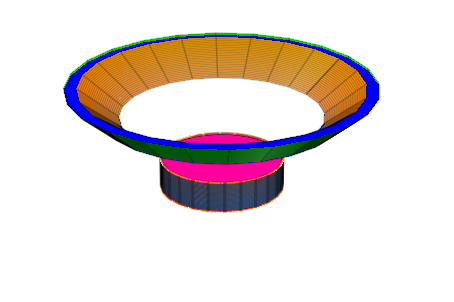
elli:=(x^2/a^2+y^2/b^2=1)
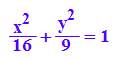
Harmonie und so weiter
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Juli 06
Quadriken und andere Rotationkörper
a:=4: b:=3:
große und kleine Halbachse
//delete a,b:
elli:=(x^2/a^2+y^2/b^2=1)
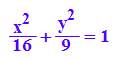
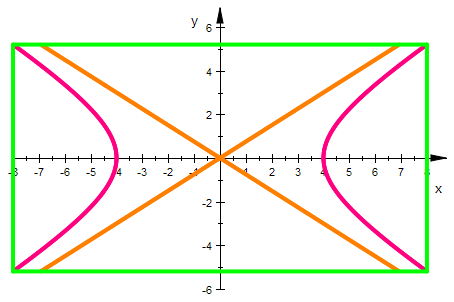
hyp:=x^2/a^2-y^2/b^2=1
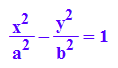
asy1:=x/a+y/b=0; asy2:=x/a-y/b=0
![]()
![]()
Graphen dazu
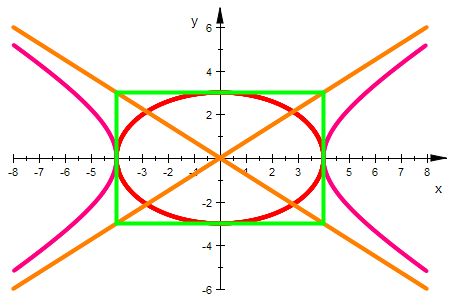
ellig:=plot::Implicit2d(elli,x=-2*a..2*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0,0]):
hypg:=plot::Implicit2d(hyp,x=-2*a..2*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0,0.5]):
asy1g:=plot::Implicit2d(asy1,x=-2*a..2*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0.5,0]):
asy2g:=plot::Implicit2d(asy2,x=-2*a..2*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0.5,0]):
kasten:=plot::Polygon2d([[a,-b],[a,b],[-a,b],[-a,-b]],
Closed=TRUE,LineWidth=1,LineColor=[0,1,0]):
plot(ellig,hypg,asy1g,asy2g,kasten)
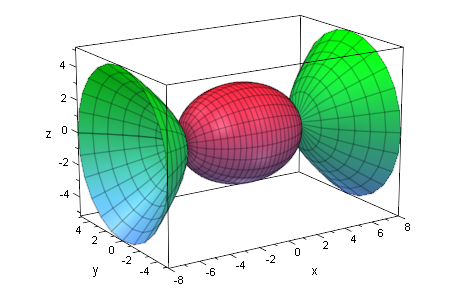
Rotationskörper bei Rotation um die x-Achse
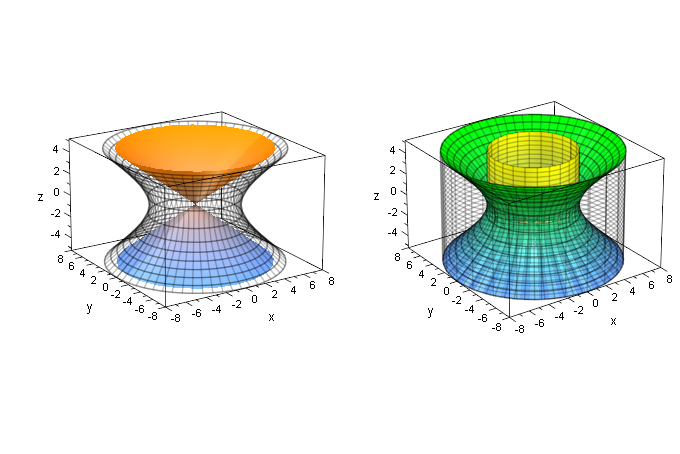
elli3d:=plot::XRotate(b*sqrt(1-x^2/a^2),x=-a..a,
Color=[1,0,0,1]):
hyp3d:=plot::XRotate(b*sqrt(-1+x^2/a^2),x=-2*a..2*a,
Color=[0,1,0,1]):
plot(elli3d,hyp3d)
Velli:=PI*int(b^2*(1-x^2/a^2), x=-a..a)
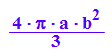
Vhyp:=2*PI*int(b^2*(-1+x^2/a^2), x=a..2*a)
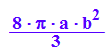
Fazit: Jede Hyperbelschale (bis 2a) ist so groß wie das Ellipsoid
elli3d::Color:=[1,0,0,1]:
elli3d::VLinesVisible:=FALSE:
zyl3d:=plot::XRotate(b,x=-a..a,
Color=[0,1,0,0.2], Filled=FALSE, LineWidth=0.8):
asy3d:=plot::XRotate(b/a*x,x=-2*a..2*a,
Color=[1,0.5,0,1]):
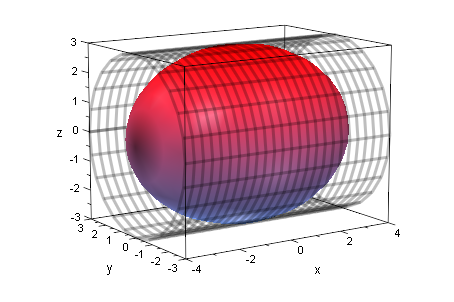
plot(elli3d,zyl3d)
delete a,b:
Velli:=PI*int(b^2*(1-x^2/a^2), x=-a..a)
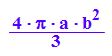
VZyl:=PI*b^2*2*a
![]()
Fazit: Das Ellipsoid nimmt in dem Zylinder 2/3 ein.
hyp3d::Color:=[1,0,1,1]:
hyp3d::ULinesVisible:=FALSE:
hyp3d::VLinesVisible:=FALSE:
asy3d::Filled:=FALSE:
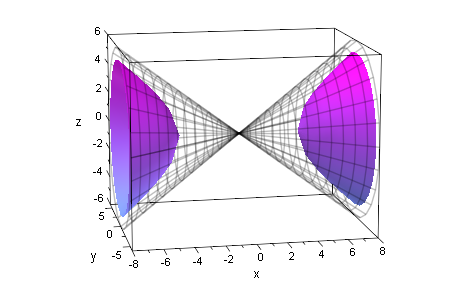
plot(asy3d,hyp3d)
Vhyp:=2*PI*int(b^2*(-1+x^2/a^2), x=a..2*a)
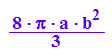
VKegdoppg:=2/3*PI*4*b^2*2*a
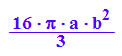
Fazit: Die Hyperboloidschalen (bis 2a) nehmen die Hälfte
des Doppelkegels ein.
a:=4:b:=3:
zyl3d:=plot::XRotate(b,x=-a..a,
Color=[0,1,0,0.2], Filled=FALSE, LineWidth=0.8):
asy3dk:=plot::XRotate(b/a*x,x=-a..a,
Color=[1,0.5,0,1],ULinesVisible=FALSE,
VLinesVisible=FALSE):
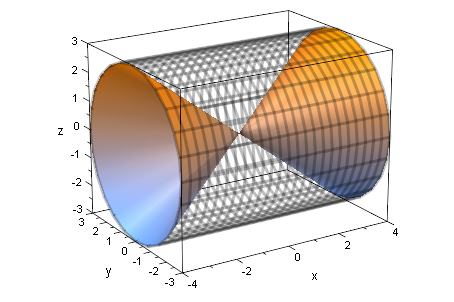
plot(asy3dk,zyl3d)
delete a,b:
VKegdoppk:=2/3*PI*b^2*a
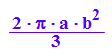
VZyl:=PI*b^2*2*a
![]()
Fazit: Der Doppelkegel nimmt 1/3 des Zylinders ein.
In den Rest passt volumenmäßig genau das Ellipsoid.
Velli:=PI*int(b^2*(1-x^2/a^2), x)
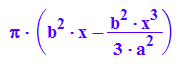
Velli:=PI*int(b^2*(1-x^2/a^2), x=-a..a)
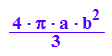
Vhyp:=2*PI*int(b^2*(-1+x^2/a^2), x=a..2*a)
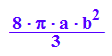
VZyl:=PI*b^2*2*a
![]()
VKegdoppk:=2/3*PI*b^2*a
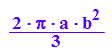
VKegdoppg:=2/3*PI*4*b^2*2*a
##################################################
Betrachtung einer Scheibe aus dem Körper zwischen dem Hyperboloid
und dem Asymptotenkegel. (Rotation um die x-Achse)
m:=-100:d:=2:c:=5:
solve(b*sqrt(-1+x^2/a^2)=m*(x-c)+b/a*c,x):
gr:=float(op(%));
![]()
c:=c+d:solve(b*sqrt(-1+x^2/a^2)=m*(x-c)+b/a*c,x):
gr2:=float(op(%));c:=5:
![]()
ring:=plot::Surface([c,r*cos(t),r*sin(t)],t=0..2*PI,
r=b*sqrt(-1+c^2/a^2)..b/a*c,Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
ring2:=plot::Surface([c+d,r*cos(t),r*sin(t)],t=0..2*PI,
r=b*sqrt(-1+(c+d)^2/a^2)..b/a*(c+d),Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
asy3dScheibe:=plot::XRotate(b/a*x,x=c..c+d,
Color=[1,0.5,0,1]):
hyp3dScheibe:=plot::XRotate(b*sqrt(-1+x^2/a^2),x=c..c+d,
Color=[0,1,0,1]):
zyl3dScheibe:=plot::XRotate(b,x=0..d,
Color=[1,0.5,0,1], LineWidth=0.8):
kreis1:=plot::Circle3d(b,[0,0,0],[1,0,0],Color=[1,0.5,0],
FillColor=[1,0,0.5],Filled=TRUE):
kreis2:=plot::Circle3d(b,[2,0,0],[1,0,0],Color=[1,0.5,0],
FillColor=[1,0,0.5], Filled=TRUE):
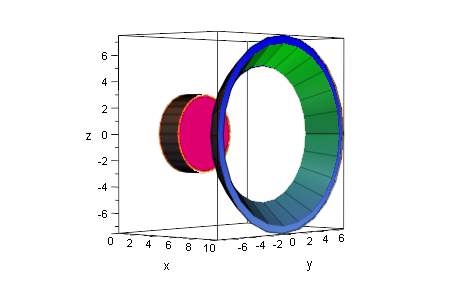
plot(kreis1, kreis2, zyl3dScheibe,
asy3dScheibe,hyp3dScheibe,ring, ring2);
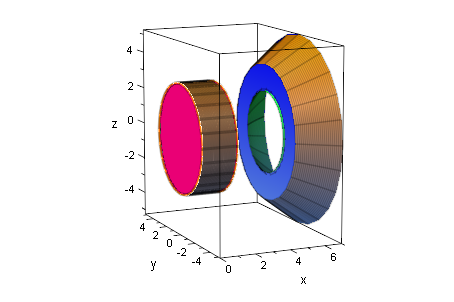
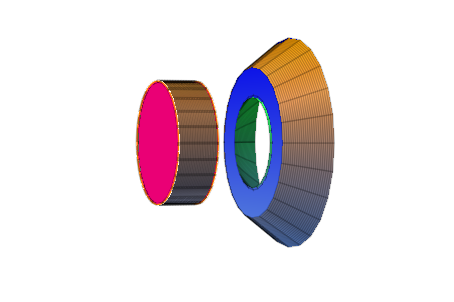
plot(kreis1, kreis2, zyl3dScheibe,
asy3dScheibe,hyp3dScheibe,ring, ring2,Axes=None);
delete a,b,c,d:
a,b,c,d,x
![]()
VKegScheibe:=1/3*PI*(b/a*(c+d))^2*(c+d)-1/3*PI *(b/a*c)^2*c
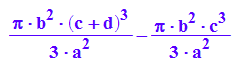
simplify(%)
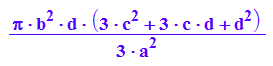
VhypScheibe:=PI*int(b^2*(-1+x^2/a^2), x=c..c+d)
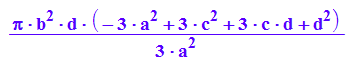
VRing:=VKegScheibe-VhypScheibe
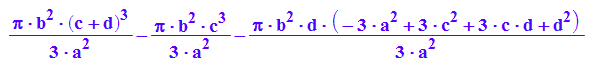
simplify(VRing)
![]()
Fazit: Ein Ring der Dicke d zwischen dem Hyperboloid
und dem Asymptoten-Kegel an beliebiger Stelle genommen
hat dasselbe Volumen wie eine Zylinderscheibe der Dicke d.
a:=4:b:=3:d:=2: delete c:
ringani:=plot::Surface([c,r*cos(t),r*sin(t)],t=0..2*PI,
r=b*sqrt(-1+c^2/a^2)..b/a*c,c=4..8,Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
ring2ani:=plot::Surface([c+d,r*cos(t),r*sin(t)],t=0..2*PI,
r=b*sqrt(-1+(c+d)^2/a^2)..b/a*(c+d),c=4..8,Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
asy3dScheibeani:=plot::XRotate(b/a*x,x=c..c+d,c=4..8,
Color=[1,0.5,0,1]):
hyp3dScheibeani:=plot::XRotate(b*sqrt(-1+x^2/a^2),x=c..c+2,c=4..8,
Color=[0,1,0,1]):
plot(kreis1,kreis2,zyl3dScheibe,hyp3dScheibeani,asy3dScheibeani,
ringani, ring2ani, AnimationStyle=BackAndForth)
Zwischen Grün (Hyperboloid)und Braun (Kegel) konstant
genau wie gleich breite Zylinderscheibe
##########################################
Rotation um die z-Achse
Version 1
Zuerst muss berechnet werden, welchen Radius der Doppelkegel hat,
der von dem einschaligen Hyperboloid, das bis x=2a geht, umfasst wird.
solve(b/a*x=b*sqrt(-1+4),x)
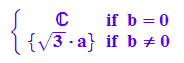
a:=4:b:=3:w3:=sqrt(3):
asy1g1:=plot::Implicit2d(asy1,x=-w3*a..w3*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0.5,0]):
asy2g1:=plot::Implicit2d(asy2,x=-w3*a..w3*a, y=-2*b..2*b,
LineWidth=1,LineColor=[1,0.5,0]):
kasten1:=plot::Polygon2d([[2*a,-w3*b],[2*a,w3*b],[-2*a,w3*b],
[-2*a,-w3*b]],Closed=TRUE,LineWidth=1,LineColor=[0,1,0]):
plot(hypg,asy1g1,asy2g1,kasten1)
Berechnung des einschaligen Hyperboloids, des stehenden
Zylinders außen und des aufrechten Doppelkegels innen.
delete a,b:
h:=sqrt(3)*b
![]()
Vhypein:=PI*int(a^2*(1+y^2/b^2), y=-h..h)
![]()
Vasyein:=2/3*PI*3*a^2*h
![]()
VZylein:=PI*a^2*2*h //Kegel bis zum Scheitel
![]()
VZyleinUm:=PI*4*a^2*2*h
![]()
a:=4:b:=3:w3:=sqrt(3):
hyp3dZo:=plot::ZRotate(b*sqrt(-1+x^2/a^2),x=-2*a..2*a,
Color=[0,1,0,1], Mesh=[30,30]):hyp3dZo2:=hyp3dZo:
hyp3dZu:=plot::ZRotate(-b*sqrt(-1+x^2/a^2),x=-2*a..2*a,
Color=[0,1,0,1],Mesh=[30,30]):hyp3dZu2:=hyp3dZu:
asy3dZ:=plot::ZRotate(b/a*x,x=-w3*a..w3*a,
Color=[1,0.5,0,1]):
asy3dZ::ULinesVisible:=FALSE:
asy3dZ::VLinesVisible:=FALSE:
hyp3dZo:=plot::modify(hyp3dZo2,Filled=FALSE):
hyp3dZu:=plot::modify(hyp3dZu2,Filled=FALSE):
ZyleinUm:=plot::Surface([2*a*cos(t),2*a*sin(t),z],t=0..2*PI,
z=-w3*b..w3*b, Color=[0,1,0,0.2]):
ZyleinUm::Filled:=FALSE:
ZyleinInn:=plot::Surface([a*cos(t),a*sin(t),z],t=0..2*PI,
z=-w3*b..w3*b, Color=[1,1,0,1]):
plot(plot::Scene3d(asy3dZ,hyp3dZo,hyp3dZu),
plot::Scene3d(ZyleinUm,hyp3dZo2,hyp3dZu2,ZyleinInn))
Fazit: Das Hyperboloid nimmt die Hälfte des umfassenden Zylinders
ein. Es ist doppelt so groß wie der Asymptotenkegel.
Der Scheitelzylinder ist genauso groß wie der Asypmtotenkegel.
##########################################
Rotation um die z-Achse
Version 2
Zuerst muss berechnet werden, bis zu welchem x das einschalige Hyperboloid rericht,
wenn der Radius des Asymptoten-Doppelkegels a ist.
hyp
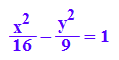
a:=4: b:=3: w2:=sqrt(2): br:=w2*a; float(w2)
![]()
![]()
ellig:=plot::Implicit2d(elli,x=-a..a, y=-b..b,
LineWidth=1,LineColor=[1,0,0]):
hypgb:=plot::Implicit2d(hyp,x=-1.414*a..1.414*a, y=-b..b,
LineWidth=1,LineColor=[1,0,0.5]):
asy1gb:=plot::Implicit2d(asy1,x=-a..a, y=-b..b,
LineWidth=1,LineColor=[1,0.5,0]):
asy2gb:=plot::Implicit2d(asy2,x=-a..a, y=-b..b,
LineWidth=1,LineColor=[1,0.5,0]):
ggb1:=plot::Implicit2d(y=b/(w2*a)*x,x=-w2*a..w2*a, y=-b..b,
LineWidth=1,LineColor=[0,0,0.5]):
ggb2:=plot::Implicit2d(y=-b/(w2*a)*x,x=-w2*a..w2*a, y=-b..b,
LineWidth=1,LineColor=[0,0,0.5]):
kastenb:=plot::Polygon2d([[br,-b],[br,b],[-br,b],[-br,-b]],
Closed=TRUE,LineWidth=1,LineColor=[0,1,0]):
plot(ellig,hypgb,asy1gb,asy2gb,ggb1,ggb2,kastenb,Scaling=Constrained):
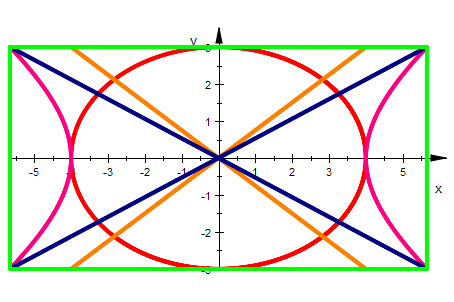
Rechnungen mit einer Höhe 2 H, es zeigt sich H=b ist ergiebig.
delete a,b:
VhypeinH:=PI*int(a^2*(1+y^2/b^2), y=-H..H)
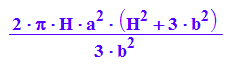
VZylH:=PI*a^2*(1+H^2/b^2)*2*H
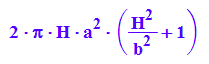
simplify(VZylH-VhypeinH)
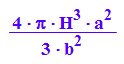
Mit beliebigem H könnte man an eine Kugel denken.
Insgesamt aber nicht griffig.
H=b wie in obiger Zeichnung
H:=b:
Vhypein:=PI*int(a^2*(1+y^2/b^2), y=-H..H)
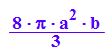
VZylH:=PI*a^2*(1+H^2/b^2)*2*H
![]()
simplify(VZylH-VhypeinH)
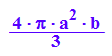
VelliZ:=PI*int(a^2*(1-y^2/b^2), y=-H..H)
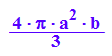
VKegb:=2/3*PI*2*a^2*b
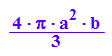
Vasyb:=2/3*PI*a^2*b
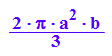
VZylbInn:=PI*a^2*b
![]()
VKasten:=(2*w2*a)^2*2*b
![]()
a:=4:b:=3:br:=sqrt(2)*a:
hyp3dZob:=plot::ZRotate(b*sqrt(-1+x^2/a^2),x=-br..br,
Color=[0,1,0,1], Mesh=[30,30]):
hyp3dZub:=plot::ZRotate(-b*sqrt(-1+x^2/a^2),x=-br..br,
Color=[0,1,0,1],Mesh=[30,30]):
asy3dZb:=plot::ZRotate(b/a*x,x=-a..a,
Color=[1,0.5,0,1]):
asy3dZb::ULinesVisible:=FALSE:
asy3dZb::VLinesVisible:=FALSE:
kegb:=plot::ZRotate(b/br*x,x=-br..br,
Color=[0.5,0,0.5,1]):
hyp3dZob::Filled:=TRUE:
hyp3dZub::Filled:=TRUE:
Zylb:=plot::Surface([br*cos(t),br*sin(t),z],t=0..2*PI,z=-b..b,
Color=[0,1,0,0.2]):
Zylb::Filled:=FALSE:
ZylbInn:=plot::Surface([a*cos(t),a*sin(t),z],t=0..2*PI,
z=-b..b, Color=[1,1,0,1]):
S1:=plot::Scene3d(asy3dZb,hyp3dZob,hyp3dZub,Zylb):
S2:=plot::Scene3d(kegb,hyp3dZob,hyp3dZub,Zylb):
S3:=plot::Scene3d(hyp3dZob,hyp3dZub,elli3d):
S4:=plot::Scene3d(hyp3dZob,hyp3dZub,elli3d,ZylbInn):
plot(S1,S2,S3,S4)
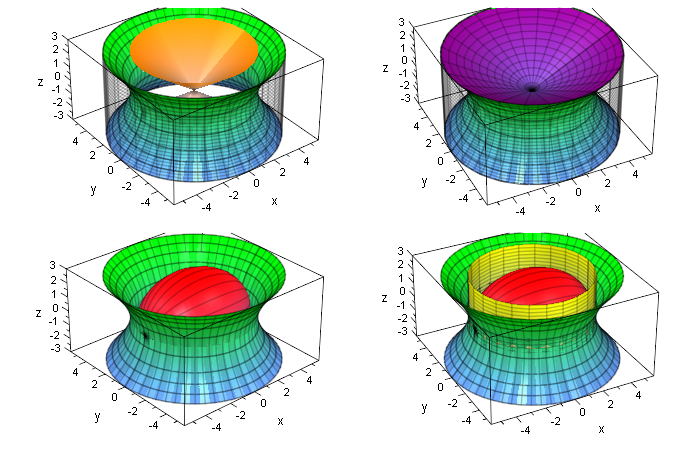
Fazit: Der Asymptotenkegel ist der Grund-Baustein B.
Ellipsoid=2 B
Zwischen Hyperboloid und Um-Zylinder = 2 B
Eingepasster Doppelkegel = 2 B
Hyperboloid= 4 B
Um-Zylinder= 6 B
ScheitelZylinder = 3/2 B
plot(asy3dZb,hyp3dZob,hyp3dZub,Zylb,ZylbInn)
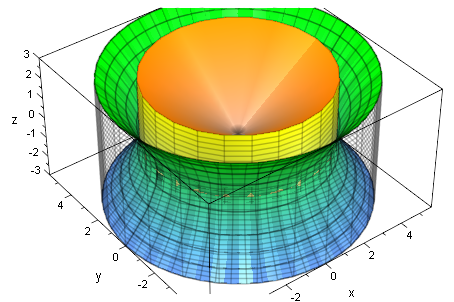
##################################################
Betrachtung einer Scheibe aus dem Körper zwischen dem Hyperboloid
und dem Asymptotenkegel. (Rotation um die y-Achse)
VKegeinScheibe:=1/3*PI*(a/b*(c+d))^2*(c+d)-1/3*PI*(a/b*c)^2*c
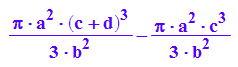
simplify(%)
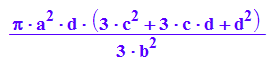
VhypeinScheibe:=PI*int(a^2*(1+y^2/b^2), y=c..c+d)
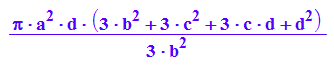
VhypeinScheibe-VKegeinScheibe
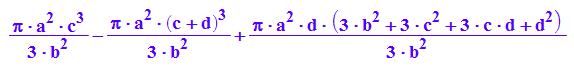
simplify(%)
![]()
Auch beim einschaligen Hyperboloid sind Scheiben der Höhe d
volumengleich zu gleichhohen Scheiben aus dem aufrechten Zylinder:
a:=4: b:=3:c:=5: d:=2:
Berechnung der x-Grenzen für das Hyberboloid
k1:=a*sqrt(1+c^2/b^2):
k2:=a*sqrt(1+(c+d)^2/b^2):
ringz:=plot::Surface([r*cos(t),r*sin(t),c],t=0..2*PI,
r=a/b*c..k1,Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
ring2z:=plot::Surface([r*cos(t),r*sin(t),c+d],t=0..2*PI,
r=a/b*(c+d)..k2,Color=[0,0,1,1],
ULinesVisible=FALSE, VLinesVisible=FALSE):
asy3dScheibez:=plot::ZRotate(b/a*x,x=a/b*c..a/b*(c+d),
Color=[1,0.5,0,1]):
hyp3dScheibez:=plot::ZRotate(b*sqrt(-1+x^2/a^2),x=k1..k2,
Color=[0,1,0,1]):
zyl3dScheibez:=plot::Surface([a*cos(t),a*sin(t),z],t=0..2*PI,
z=0..d, Color=[1,0.5,0,1], LineWidth=0.8):
kreis1z:=plot::Circle3d(a,[0,0,0],[0,0,1],Color=[1,0.5,0],
FillColor=[1,0,0.5],Filled=TRUE):
kreis2z:=plot::Circle3d(a,[0,0,d],[0,0,1],Color=[1,0.5,0],
FillColor=[1,0,0.5], Filled=TRUE):
plot(kreis1z, kreis2z, zyl3dScheibez,
asy3dScheibez,hyp3dScheibez,ringz, ring2z);
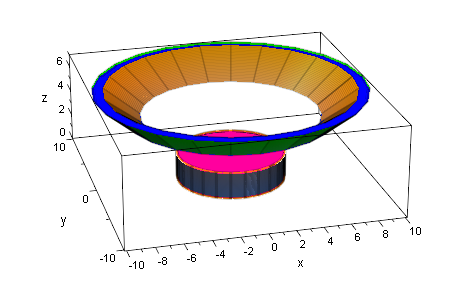
plot(kreis1z, kreis2z, zyl3dScheibez,
asy3dScheibez,hyp3dScheibez,ringz, ring2z, Axes=None);