plotfunc3d(x*y)
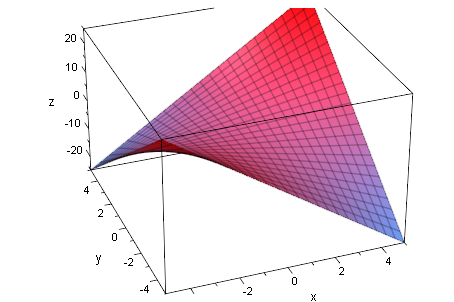
Hyperbololisches Paraboloid
Prof. Dr. Dörte Haftendorn, MuPAD 4, Juni 08 Update 29. Juni 08
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
plotfunc3d(x*y)

ger:=plot::Curve3d([-t,a,-a*t+25],t=-5..5,a=-5..5,
LineWidth=1,LineColor=[0,1,0]);
hypar:=plot::Function3d(x*y+25,x=-5..5,y=-5..5);
![]()
![]()
plot(ger,hypar)
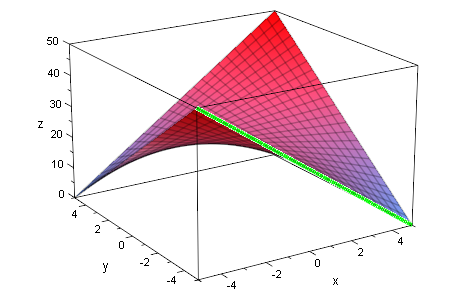

Das hyperbolische Paraboloid wird durch eine "geschraubte" Gerade
erzeugt.
##################################################
Volumen unter diesem Dach bis zur Nullebene
int(int(x*y+25, x=-5..5), y=-5..5)
![]()
Das ist genau der habe Kasten.
#####################################################
Ansehen der Schnitte mit waagerechten Ebenen.
eb:=plot::Function3d(b,x=-5..5,y=-5..5,b=0..50,FillColor=[0,1,0], FillColor2=[1,1,0] );
![]()
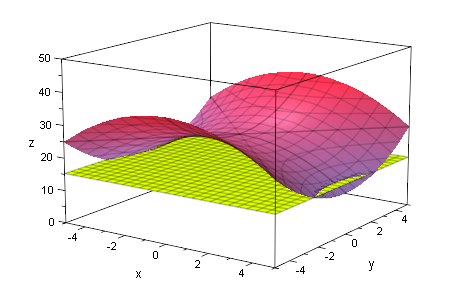
plot(hypar,eb)
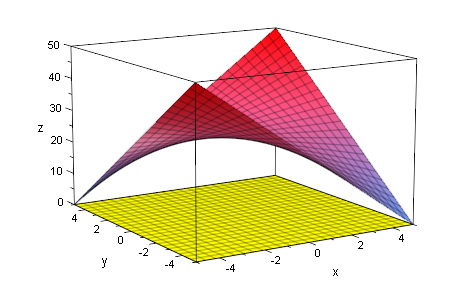

Diese Schnitte sind Hyperbeln.
################################################################
Drehen um PI/4
A:=matrix([[cos(t),-sin(t),0],[sin(t),cos(t),0],[0,0,1]])|t=PI/4;
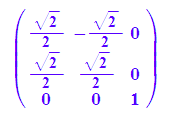
hypparvek:=matrix([t,r,t*r])
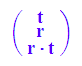
hyd:=A*hypparvek
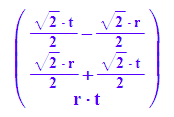
X:=hyd[1]; Y:=hyd[2]; Z:=hyd[3]
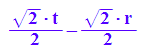
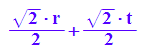
![]()
(X+Y)*(X-Y)
![]()
Also gilt
hydreh:=x^2-y^2=2*z;
![]()
Noch um 25 nach oben schieben
hyparim:=plot::Implicit3d(x^2-y^2+2*(z-25)=0,x=-5..5, y=-5..5,z=0..50)
![]()
plot(hyparim,eb)

Auch die wandernde Grade kann man drehen um 45°
gerdre:=A*matrix([-t,a,-a*t+25])
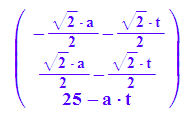
gerdr:=plot::Curve3d(gerdre,t=-5..5,a=-5..5,
LineWidth=1,LineColor=[0,1,0]);
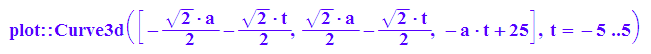
plot(hyparim,gerdr)
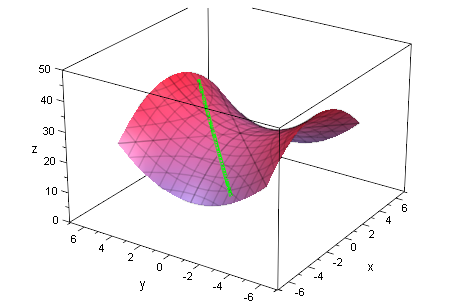

Nun sind die Hauptschnitte also Parabeln, die Schnitte mit
horizontalen Ebenen sind immernoch Hyperbeln. darum also der Name
hyperbolisches Paraboloid
Natürlich liegt die gedrehte Gerade auch darauf.
Flächen, die durch bewegte Geraden entstehen heißen Regelflächen
Sie lassen sich leicht in Beton bauen.
Das hyperbolische Paraboloid ist also eine Regelfläche,
der Kegel, auch der Kegelstumpf ist also eine Regelfläche,
die Schraubenfläche ist also eine Regelfläche,
das einschalige Hyperboloid ist also eine Regelfläche,