f:=4:c:=2:
hy:=plot::Implicit3d(x^2/f^2+y^2/f^2-z^2/(f^2*c^2)=1,
x=-10..10,y=-10..10,z=-10..10, Mesh=[20,20,20]):
ger:=plot::Curve3d([f,r,r*c],r=-5..5,
LineWidth=1,LineColor=[0,1,0]);
![]()
Einschaliges Hyperboloid
Prof. Dr. Dörte Haftendorn, MuPAD 4, Juni 08 Update 29. Juni 08
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Eine Gerade, die windschief zur z-Achse ist, dreht sich um die z-Achse.
Erst ist hier das Ergebnis gezeichnet.
f:=4:c:=2:
hy:=plot::Implicit3d(x^2/f^2+y^2/f^2-z^2/(f^2*c^2)=1,
x=-10..10,y=-10..10,z=-10..10, Mesh=[20,20,20]):
ger:=plot::Curve3d([f,r,r*c],r=-5..5,
LineWidth=1,LineColor=[0,1,0]);
![]()
Rotations-Hyperboloid mit erzeugender Gerade, letztere in Parameterdarstellung
plot(hy,ger)
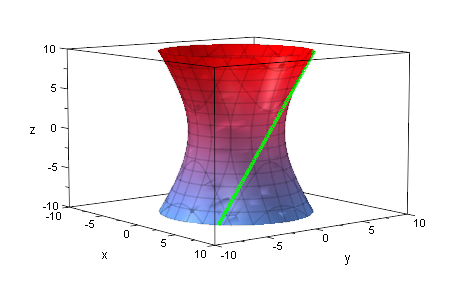
Nun soll die Gerade sich drehen um die z-Achse
A:=matrix([[cos(t),-sin(t),0],[sin(t),cos(t),0],[0,0,1]]);
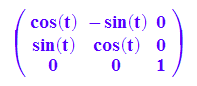
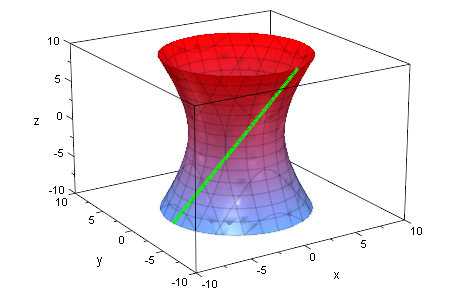
gera:=plot::Curve3d([f*cos(t)-r*sin(t),f*sin(t)+r*cos(t),r*c],r=-5..5, t=0..2*PI, LineWidth=1, LineColor=[0,1,0]):
plot(hy,gera)

Natürlich ist der Einheitsvektor der z-Achse der Eigenvektor der Matrix A
zum Eigenwert 1.
Ev:= linalg::eigenvectors(A)
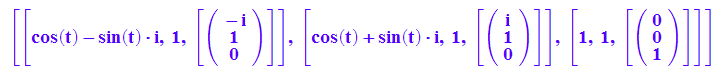
Volumenbrechnung
Für y=0 wird nach x^2 aufgelöst, der dann rechts stehende Term ist der, der über z zu integrieren ist.
hold(x^2/f^2+y^2/f^2-z^2/(f^2*c^2)=1);
hold(x^2=f^2+z^2/c^2)
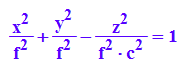
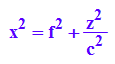
2*PI*int(f^2+z^2/c^2, z);
2*PI*int(f^2+z^2/c^2, z=0..10);
Vhyp:=float(%/PI)*PI
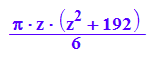
![]()
![]()
Berechnung des oberen Radius bei Höhe 10 von der Mitte aus.
hyp:=x^2/f^2+y^2/f^2-z^2/(f^2*c^2)=1
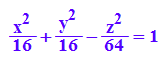
solve((hyp|z=10)|y=0,x);
solve((hyp|z=-10)|y=0,x);
![]()
![]()
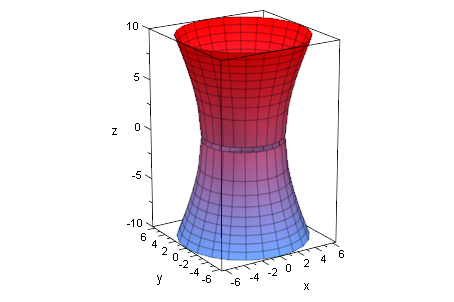
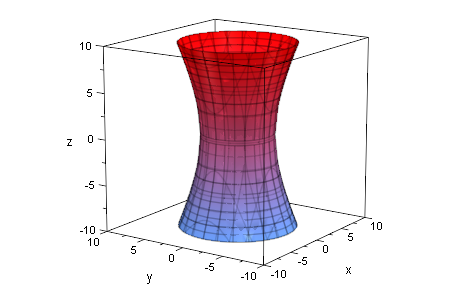
Das durch Rotationsbilder erzeugte Hyperboloid passt genau.
ob:=plot::ZRotate(c*sqrt(x^2-f^2),x=0..sqrt(41)):
unt:=plot::ZRotate(-c*sqrt(x^2-f^2),x=0..sqrt(41)):
plot(ob,unt);
plot(ob,unt, hy)
Volumen eines umfassenden Zylinders
oder eines innen liegenden Kegels
Vzyl:=PI*41*20;
Vkeg:=2*PI*41*10/3;
2.0*PI*41*10/3;
![]()
![]()
![]()
Berechnung der beiden Kegelstümpfe
kleinerer Radius
solve((hyp|z=0)|y=0,x)
![]()
Kegelstumpf-Volumenformel
hold(Vst=PI/3*(R^2+r*R+r^2)*h)
![]()
2 solche Stümpfe
2*float(1/3*(41+4*sqrt(41)+16)*10)*PI;
Vhyp
![]()
![]()
Das passt sehr schön so.