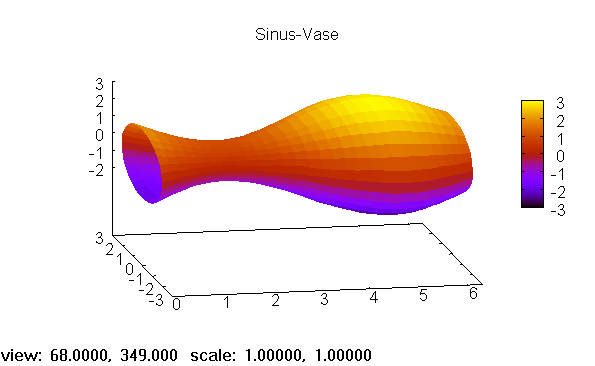
Sinustorte, Rotation um x- und z-Achse
Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Dez 2010
0.1 Handlinghilfen
0.2 Inhalt, auch zum Lernen von 3D-Zeichenmethoden
1 Schnelle Zeichen-Methoden für Einzelobjekte
1.1 Rotation um die x-Achse
1.2 Rotation um die z-Achse
2 Erweiterte Zeichen-Methoden für mehrere Objekte
2.1 Erzeugung von Grafikobjekten
2.2 Mehrere Objekte in einem Bild
2.3 Mehrere Objekttypen in einem Bild
2.4 Weitere zu den Zeichenoptionen
3 Berechnungen der Volumina der Rotationskörper
3.1 Rotation um die x-Achse
3.2 Rotatiom um die z-Achse Methode Zylinderscheibchen
3.3 Rotation um die z-Achse Methode Hohlzylinderchen
0.3 Grundlage
--> load(draw)$
Mit diesem Befehl wird ein Package geladen, das man für
das erweitere Zeichnen braucht.
Mit Markieren von draw und F1 gelangt man in die Hilfe zu draw.
Die Zeichnung erscheint in einem Extrafenster "gnuplot graph".
Oben links ist ein Icon mit Pulldown-Menu unter Options gibt es
"ins Clippboard", vorher am besten kleiner ziehen. Man muss dann
den Gnuplot schließen, damit man weiterarbeiten kann.
Dann kann man die Zeichnung hier in der Maximaseite einfügen.
Achtung, später unbedingt als wxmx speichern, sonst verschwinden
die Zeichnungen.
1 Schnelle Methoden für Einzelobjekte
1.1 Schnelle Zeichenmethode, Rotation um x-Achse
Mit einer Begrenzungsfunktion f
--> f(x):=2-sin(x)$
-->
draw3d(title = "Sinus-Vase",
surface_hide = true,
enhanced3d=true,
parametric_surface(x,
-f(x)*sin(t),
f(x)*cos(t),
t, 0, 2*%pi, x, 0, 2*%pi) )$
Figure 1:

1.2 Schnelle Zeichenmethode, Rotation um die z-Achse
Es ist sinnvoll, "um z-Achse" zu sagen, da sich das Bild dann in die
übliche Raumdarstelung einfügt.
-->
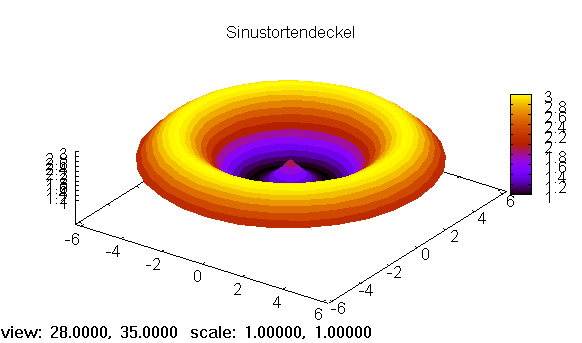
draw3d(title = "Sinustortendeckel",
surface_hide = true,
enhanced3d=true,
parametric_surface(x *cos(t),
x*sin(t),
f(x),
t, 0, 2*%pi, x, 0, 2*%pi) )$
Figure 2:
2 Erweiterte Mathoden für mehrere Objekte
2.1 Erzeugung von Grafik-Objekten
Mit gr3d(optionen, objekttyp) werden sie erzeugt.
Die Erzeugung bewirkt noch keine Darstellung.
-->
deckel:gr3d(title = "Sinustortendeckel",
surface_hide = true,
enhanced3d=true,
parametric_surface(x *cos(t),
x*sin(t),
f(x),
t, 0, 2*%pi, x, 0, 2*%pi))$
-->
rand:gr3d(title = "Sinustortenrand",
surface_hide = true,
enhanced3d=true,
parametric_surface(2*%pi *cos(t),
2*%pi*sin(t),
z,
t, 0, 2*%pi, z, 0, 2))$
Der draw-Befehl stellt die Objekte dar.
--> draw(deckel,rand)$
Figure 3:
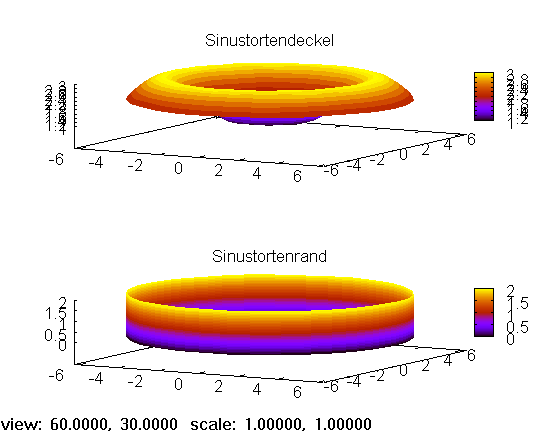
2.2 Mehrere Objekte in demselben Bild
Wenn man mehrere Objekte in ein und demselben Bild darstellen will,
schreibt man sie alle in ein einziges Grafikobjekt.
-->
torte:gr3d(title = "Sinustorte",
surface_hide = true,
enhanced3d=true,
parametric_surface(x *cos(t),
x*sin(t),
f(x),
t, 0, 2*%pi, x, 0, 2*%pi),
parametric_surface(2*%pi *cos(t),
2*%pi*sin(t),
z,
t, 0, 2*%pi, z, 0, 2))$
--> draw(torte)$
Figure 4:
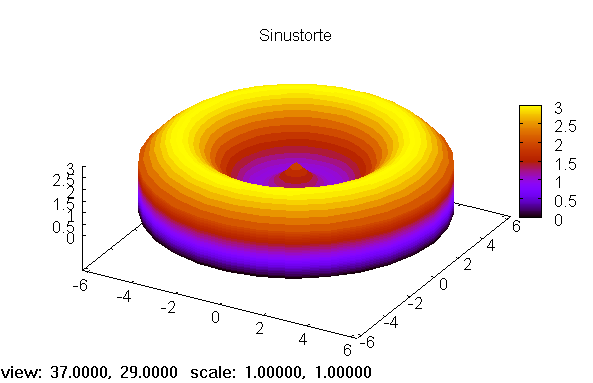
2.3 Mehrere Objekttypen in demselben Bild
Das sieht schon gut aus. Nun wäre noch das erzeugende Kurvenstück
als Raumkurve hilfreich. Es wird noch eingefügt und die
dafür benötigten Optionen stehen davor.
-->
torte_plus:gr3d(title = "Sinustorte",
surface_hide = true,
enhanced3d=true,
parametric_surface(x *cos(t),
x*sin(t),
f(x),
t, 0, 2*%pi, x, 0, 2*%pi),
parametric_surface(2*%pi *cos(t),
2*%pi*sin(t),
z,
t, 0, 2*%pi, z, 0, 2),
surface_hide=false,
enhanced3d=false,
line_width=3,
color=black,
parametric(x ,
0,
f(x),
x, 0, 2*%pi))$
--> draw(torte_plus)$
Figure 5:
Damit kann man zufrieden sein. Im gnuplot kann man die Grafik bewegen,
aber nach dem Transport über das Clippbord natürlich nicht mehr.
Dann ist es nur ein Bild.
2.4 Weiteres zu den Optionen
surface_hide sorgt dafür, dass man Verdecktes nicht sieht.
enhanced=true sorgt für die Farben entsprechend der Höhenlage.
Man kann die Farben auch durch einen Term eines Parameters steuern.
rot_horizontal und rot_vertical beziegen sich auf die Raumrichtung,
aus der man die Grafik betrachtet. Hat man interaktiv eine gute Richtung
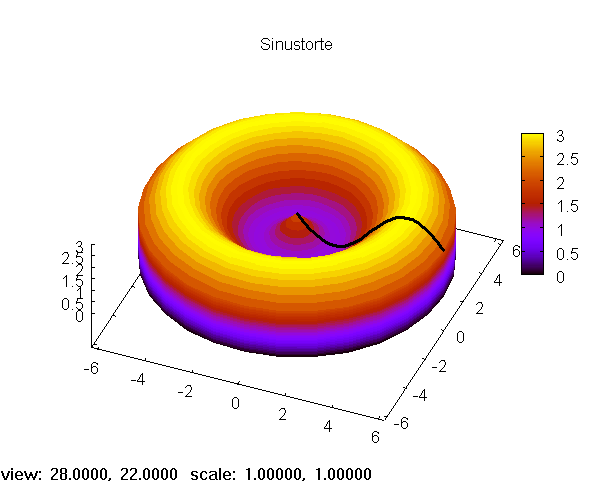
gefunden (wie oben bei View zu sehen), kann man sie dauerhaft eintragen.
-->
torte_plus:gr3d(title = "Sinustorte",
rot_horizontal=28, rot_vertical=22,
surface_hide = true, enhanced3d=true,
parametric_surface(x *cos(t),
x*sin(t),
f(x),
t, 0, 2*%pi, x, 0, 2*%pi),
parametric_surface(2*%pi *cos(t),
2*%pi*sin(t),
z,
t, 0, 2*%pi, z, 0, 2),
surface_hide=false, enhanced3d=false,
line_width=3, color=black,
parametric(x ,
0,
f(x),
x, 0, 2*%pi))$
-->
draw(torte_plus)$
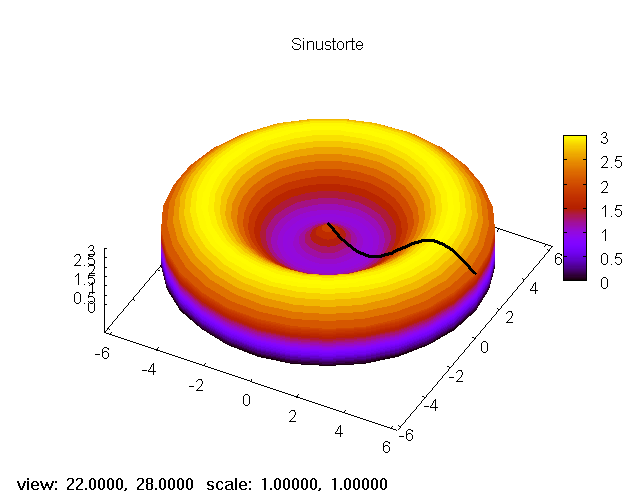
Die Zeichnung erscheint in einem Extrafenster "gnuplot graph".
Oben links ist ein Icon mit Pulldown-Menu unter Options gibt es
"ins Clippboard", vorher am besten kleiner ziehen.
Dann kann man die zeichnung hier einfügen.
Achtung, später unbedingt als wxmx speichern, sonst verschwinden
die Zeichnungen.
3 Berechnung der Volumina
3.1 Rotation um die x-Achse
-->
f(x);
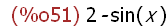
-->
wxplot2d([f(x)], [x,0,2*%pi], [y,0,3.5])$
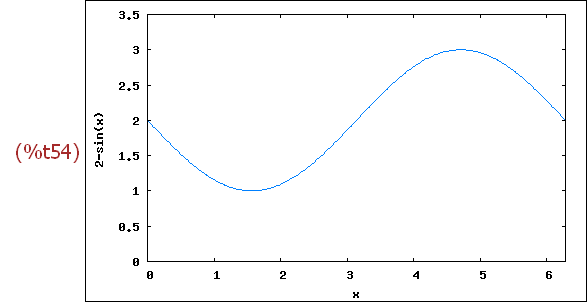
--> Vx(x_term,x,a,b):=%pi*integrate(x_term^2,x,a,b)$
-->
integrate(%pi*f(x)^2, x, 0, 2*%pi);
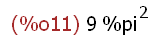
-->
Vx(f(x),x,0,2*%pi);
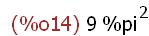
3.2 Rotation um die z-Achse, Zylinderscheibchen
Diese Methode ist hier nicht gut anwendbar, da die Funktion nicht
umkehrbar ist.
--> Vy(y_term,y,a,b):=%pi*integrate(y_term^2,y,y_a,y_b)$
Man kann hier allenfalls von 0 bis PI/2 in der Originalfigur gehen
-->
wxplot2d([asin(2-x)], [x,1,2])$
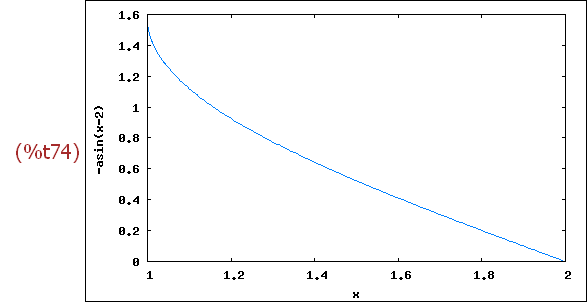
-->
%pi*integrate(asin(2-y),y,1,2) /*aber das nürtzt nichts, Quadrat fehlt*/;
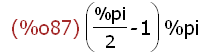
Man muss direkt überlegen, dass das gesuchte Volumen ist:
-->
integrate(asin(x)^2,x);
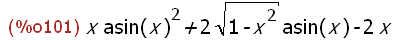
Bei Rotation um die x-Achse
-->
wxplot2d([asin(x)], [x,0,1], [y,0,%pi/2])$
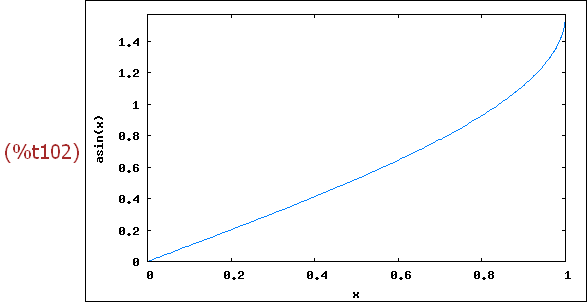
-->
vol:%pi*integrate(asin(x)^2,x,0,1);%,numer;

Mit Unterteil
-->
%pi*(%pi^2)/4*1;
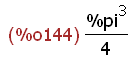
-->
vol +%;expand(%);%,numer;

Dieses Ergebnis ergibt sich mit der unteren Methode 3.3 viel
einfacher.
Und mit der Quadrierung geht es nicht in der verschobenen Form.
-->
Vy(asin(2-y),y,1,2);
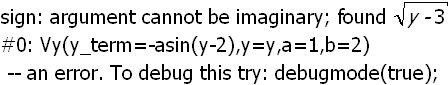
3.3 Rotation um die z-Achse, Hohlzylinderchen
--> Vz(x_term,x,a,b):=2*%pi*integrate(x*x_term,x,a,b)$
-->
vol:Vz(f(x),x,0,2*%pi); expand(vol);factor(vol);vol,numer;

Zwei Vergleichszylinder
(%i5)
%pi*(2*%pi)^2, numer;
%*3 ;
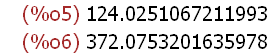
3.4 Mit Hohlzylindern im umkehrbaren Bereich
-->
Vz(f(x),x,0,%pi/2); expand(%);factor(%);%,numer;

Das ist genau der oben viel mühsamer erzeugte Wert.