xx:=t->cos(t)^3;
yy:=t->sin(t)^3;
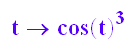
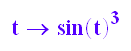
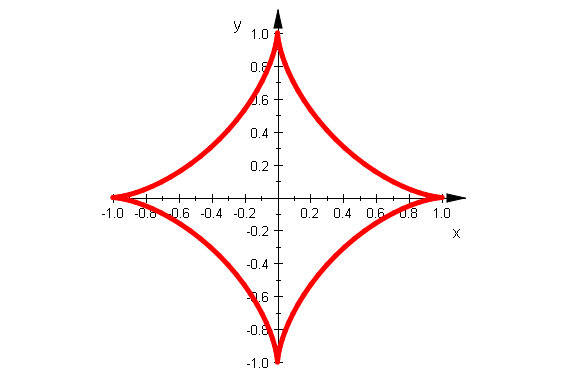
Astroide
Prof. Dr. Dörte Haftendorn, Juni 09 Update 19.06.09
www.mathematik-verstehen.de https://mathe.web.leuphana.de
##################################################################
xx:=t->cos(t)^3;
yy:=t->sin(t)^3;
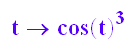
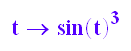
astro:=plot::Curve2d([cos(t)^3,sin(t)^3],t=0..2*PI, Scaling=Constrained, LineWidth=1,LineColor=[1,0,0]):
plot(astro)
yy'(t);xx'(t);
yy'(t)/xx'(t)//Steigung bei t
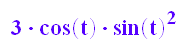
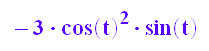
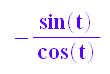
######################
Fläche der Astroide
2*int(yy'(t)*xx(t)-yy(t)*xx'(t), t);
2*int(yy'(t)*xx(t)-yy(t)*xx'(t), t=0..PI/2);
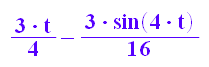

Mehr von Hand:
int(sin(t)^2*cos(t)^4, t);
int(sin(t)^4*cos(t)^2, t);
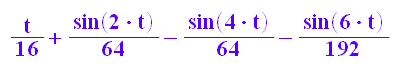
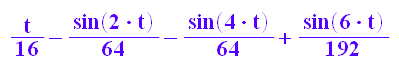
float(3/8*PI)
![]()
6*int(sin(t)^2*cos(t)^4+sin(t)^4*cos(t)^2, t=0..PI/2);

##############################
Länge der Astroide
4*int(sqrt(xx'(t)^2+yy'(t)^2), t);
L:=4*int(sqrt(xx'(t)^2+yy'(t)^2), t=0..PI/2)
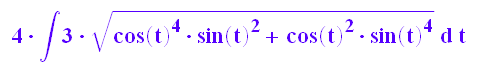
![]()
Bei dem Integral muss man cos*sin herausziehen, dann geht es leicht.
##########################################
xx:=t->cos(t)^3;
yy:=t->sin(t)^3
astro:=plot::Curve2d([cos(t)^3,sin(t)^3],t=0..2*PI, Scaling=Constrained, LineWidth=1,LineColor=[1,0,0]):
kr:=plot::Circle2d(1/2,[0,0],Filled=TRUE, Scaling=Constrained):
Gk:=plot::Circle2d(1,[0,0], Scaling=Constrained,LineColor=[0,1,0,0.5], LineWidth=1):
plot(Gk,kr,astro)
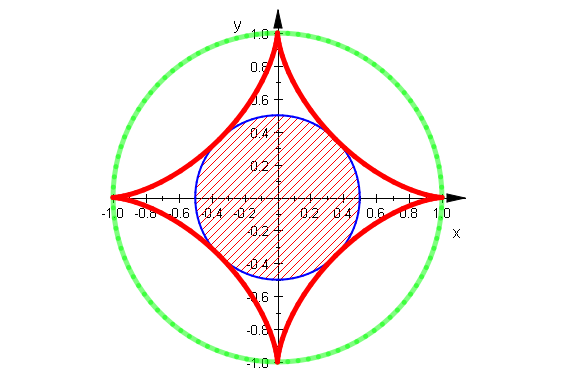
Die Hälfte des kleinen Kreises kann man auf die vier Zipfel
der Astroide verteilen. Sie ist als anderthalb mal so groß wie der Kreis.
Der kleine Keis und die Astoide zusammen sind genau so groß wie
die vier grünen Zigarren.