F:=x->x^2*cos(PI/x^2)
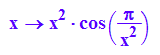
Stetige Stammfunktion und doch keine volle Integrierbarkeit
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Sept 07 Update 21.09.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Hier gibt es überall stetige und differenzierbare Funktionen, die man
"nicht durchzeichnen kann".
F:=x->x^2*cos(PI/x^2)
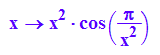
plotfunc2d(x^2,F(x),-x^2,x=-2..2,ViewingBoxYRange=-1..1)
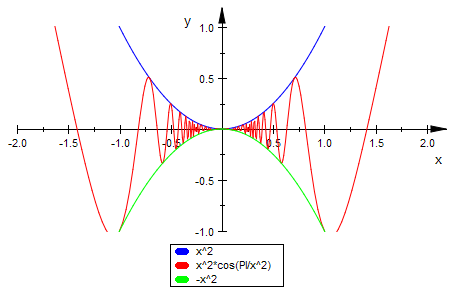
Ersichtlich ist F stetig
F'(x)
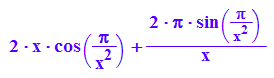
Der Differentialquotient bei x=0 existiert.
limit(F(h)/h,h=0)
![]()
F ist auch überall differenzierbar.
Dennoch hat die Ableitung eine Unstetigkeitsstelle, x=0, und ist nicht beschränkt.
Zudem oszilliert auch f
f:=x-->F'(x)
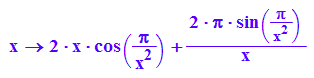
plotfunc2d(2*x+2*PI/x,f(x),-2*x-2*PI/x,x=-2..2,ViewingBoxYRange=-50..50)
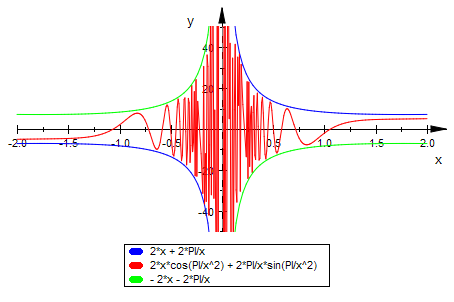
int(f(x), x)
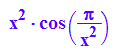
int(f(x), x);
int(f(x), x=c..1/2);
int(f(x), x=0..1/2);
F(1/2);
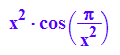
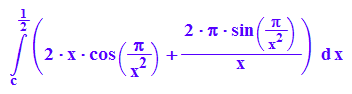
![]()
![]()
Obwohl f alsobei x=0 bis ins Unendliche wächst und obwohl die Fläche
unter den berandenden Funktionen unendlich ist, hat das uneigentliche Integral
einen endlichen Wert.
####################
Nun drücke ich den Graphen bei 0 noch stärker zusammen
F:=x->x^3*cos(PI/x^2)
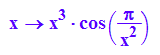
plotfunc2d(x^3,F(x),-x^3,x=-2..2,ViewingBoxYRange=-1..1)
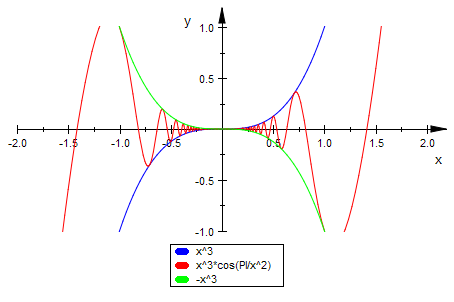
F'(x)
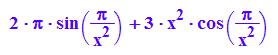
Der Differentialquotient bei x=0 existiert.
limit(F(h)/h,h=0)
![]()
Dennoch ist die Ableitung nicht stetig in 0
f:=x-->F'(x)
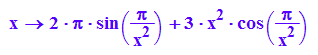
plotfunc2d(2*x^2+2*PI,f(x),-2*x^2-2*PI,x=-2..2,ViewingBoxYRange=-50..50)
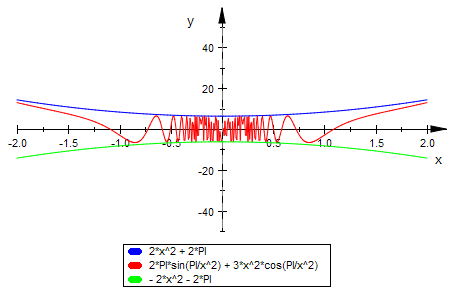
Dennoch ist f Riemann-integrierbar
int(f(x), x);
int(f(x), x=0..0.5)
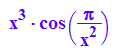
![]()
####################
Nun drücke ich den Graphen bei 0 noch stärker zusammen
F:=x->x^4*cos(PI/x^2)
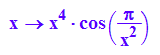
plotfunc2d(x^4,F(x),-x^4,x=-2..2,ViewingBoxYRange=-1..1)
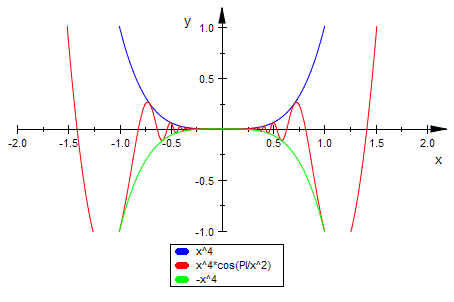
F'(x)
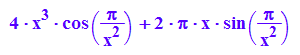
Der Differentialquotient bei x=0 existiert.
limit(F(h)/h,h=0)
![]()
Nun aber ist die Ableitung stetig in 0
f:=x-->F'(x)
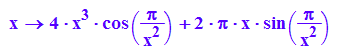
plotfunc2d(4*x^3+2*PI*x,f(x),-4*x^3-2*PI*x,x=-2..2,ViewingBoxYRange=-10..10)
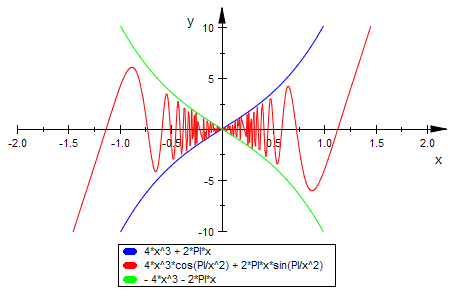
int(f(x), x)
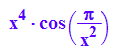
F:=x->x^2*cos(1/x);
F'(x)
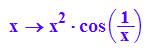
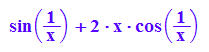
plotfunc2d(F'(x))
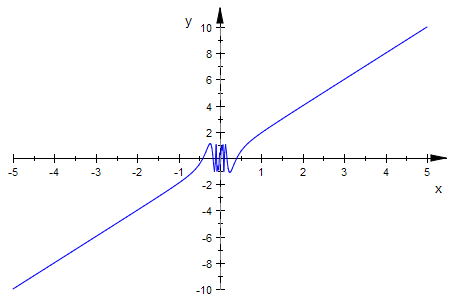
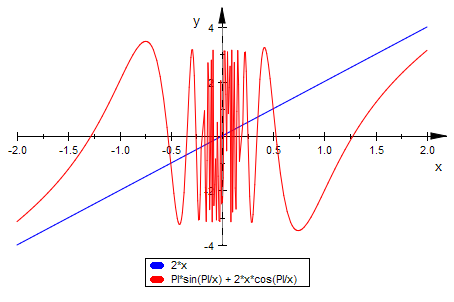
Mein altes Beispiel: Sinuswunderdinge
F:=x->x^2*cos(PI/x)
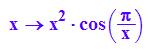
plotfunc2d(x^2,F(x),-x^2,x=-2..2,ViewingBoxYRange=-1..1)
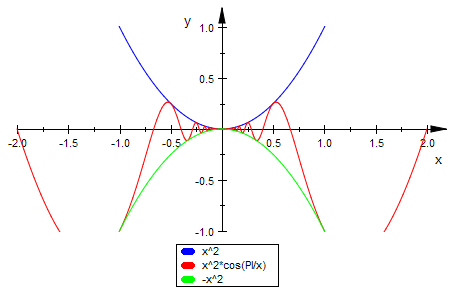
F'(x)
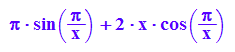
Der Differentialquotient bei x=0 existiert.
limit(F(h)/h,h=0)
![]()
Nun aber ist die Ableitung unstetig
f:=x-->F'(x)
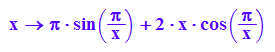
plotfunc2d(2*x,f(x),x=-2..2)
int(f(x), x);
int(f(x), x=0..1/2);
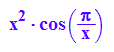
![]()