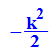Ein weiterer Eulerkasten
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Feb. 06 Update 24.02.06
Web: www.mathematik-verstehen.de www.uni-lueneburg.de/ing-math
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben
#############################
Angeregt durch meine Aufgabe "Eulerkasten" haben meine Studierenden
Anke Freitag, Andre Fritz und Katja Konradt auch bei einer anderen e-Funktion
einen solchen Kasten entdeckt.

• f:=(x,k)->exp(x)*(exp(x)-k)

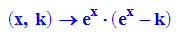
• plotfunc2d(f(x,k)$ k=-2..4,x=-2..4,ViewingBox=[-2..2,-5..5])

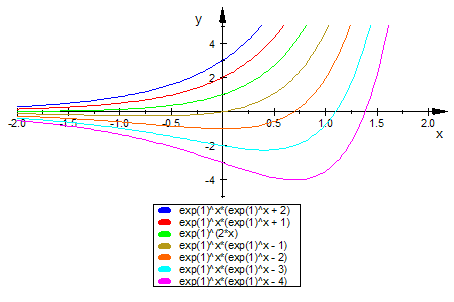
• plotfunc2d(f(x,k),x=-5..3,k=0..4,ViewingBox=[-2..2,-5..5])

• ff:=diff(f(x,k), x)

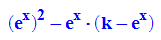
• //assume({x,k},Type::Real)

Hier sieht man mal wieder, dass man ohne eigen Kompetenzen
nicht auskommt.

• solve(ff=0,x)

von Hand

• xe:=ln(k/2)

• expand(xe)

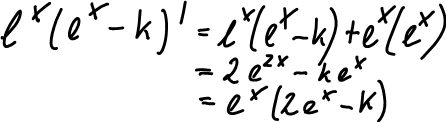
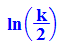
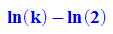
Extremwert ist:

• ye:=f(xe,k)

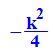
Zweite Ableitung

• fff:=diff(f(x,k), x,x)

• expand(fff)

• solve(%=0,x)

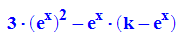
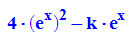
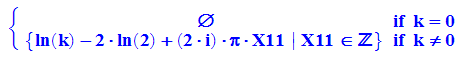
• simplify(subs(fff, x = ln(k)-2*ln(2)))

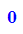
Wendestelle ist:

• xw:=ln(k)-2*ln(2)

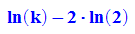
Ordinate des Wendepunktes ist:

• yw:=simplify(expand(f(xw,k)))

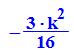
Wendesteigung ist:

• wst:=simplify(subs(ff, x = xw))

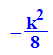
Die Wendetangente ist:

• wt:=x->wst*(x-xw)+yw;
  wt(x)

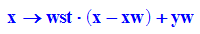
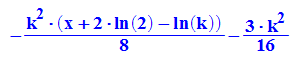
Nullstelle des Wendetangente:

• solve(wt(x)=0,x)

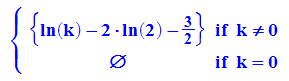
Schnitt der Wendetangente mit der Extremallinie:

• solve(wt(x)=ye,x)

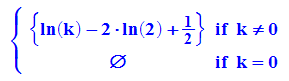
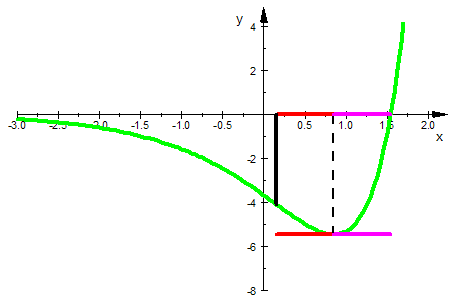
Es gibt also einen Kasten der Breite 2 und der Höhe ,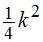
den die Wendetangente mit x-Achse und Extremallinie definiert.
Auf dessen unterer rechter Viertelstelle liegt der Wendepunkt.
Diese Eigenschaft hat auch die auf der Seite "Eulerkasten" beschriebene
Funktion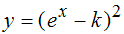
Auch dort wird die Höhe durch Asyptote und Extemallinie definiert,
ist aber .

• gf:=plot::Function2d(f(x,4),x=-3..2,ViewingBox=[-3..2,-4..4],
              LineWidth=1,LineColor=[0,1,0]):

• gwt:=plot::Function2d(subs(wt(x), k= 4),x=-3..2,
              LineWidth=0.6,LineColor=[0,0,1]):
  plot(gf,gwt)

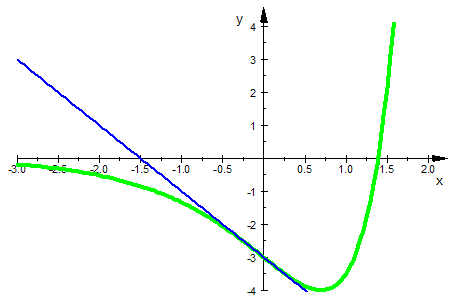
• kasten:=plot::Polygon2d(subs([[xw-3/2,0],[xw+1/2,0],
                         [xw+1/2,ye],[xw-3/2,ye],
                         [xw-3/2,0] ],k=4), Filled=TRUE):
  plot(kasten,gf,gwt)

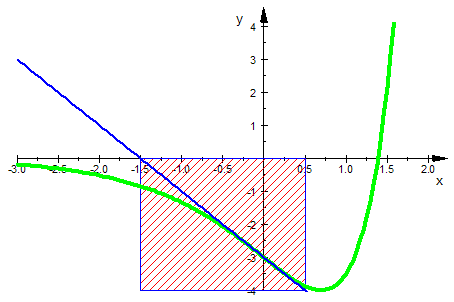
• gfani:=plot::Function2d(f(x,k),x=-3..2,k=1..5,
  ViewingBox=[-3..2,-8..4],LineWidth=1,LineColor=[0,1,0]):
  gwtani:=plot::Function2d(wt(x),x=-3..2,k=1..5
  ,LineWidth=0.6,LineColor=[0,0,1]):
  gex:=plot::Line2d([xw,ye],[xw+ln(2),ye],k=1..5
  ,LineWidth=1,LineColor=[1,0,0]):
  gexo:=plot::Line2d([xw,0],[xw+ln(2),0],k=1..5
  ,LineWidth=1,LineColor=[1,0,0]):
  gexs:=plot::Line2d([xe,0],[xe,ye],k=1..5
  ,LineWidth=0.5,LineColor=[0,0,0], LineStyle=Dashed):
  gnu:=plot::Line2d([xe,0],[ln(k),0],k=1..5
  ,LineWidth=1,LineColor=[1,0,1]):
  gnuu:=plot::Line2d([xe,ye],[ln(k),ye],k=1..5
  ,LineWidth=1,LineColor=[1,0,1]):
  gwp:=plot::Line2d([xw,0],[xw,yw],k=1..5
  ,LineWidth=1,LineColor=[0,0,0]):
  kastenani:=plot::Polygon2d([[xw-3/2,0],[xw+1/2,0],
                         [xw+1/2,ye],[xw-3/2,ye],
                         [xw-3/2,0] ],k=1..5,Filled=TRUE ):
  plot(gfani,gwtani, kastenani,gex,gexo,gexs,gnu,gnuu,gwp);
  

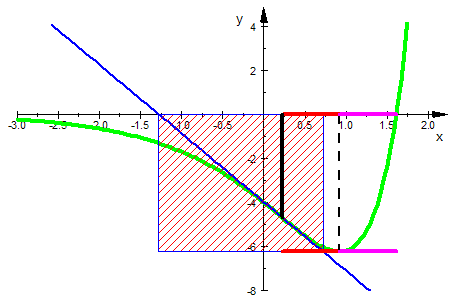
Achtung, die obere und die untere Graphik animieren.

• plot(gfani, gex,gexo,gexs,gnu,gnuu,gwp);

Untersuchung der Flächen:

• int(f(x,k), x)

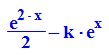
• int(f(x,k), x=-infinity..ln(k))

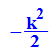
Und das ist wieder genau die Kastenfläche

• 2*ye

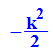
• gfklein:=plot::Function2d(f(x,4),x=-3..ln(4),ViewingBox=[-3..2,-4..4],
              LineWidth=1,LineColor=[0,1,0]):
  wpkt:=plot::Point2d(subs([xw,yw],k=4),
             PointSize=3, PointStyle=FilledDiamonds):
  inte:=plot::Integral(gfklein):plot(inte,gf,kasten,gwt,wpkt)

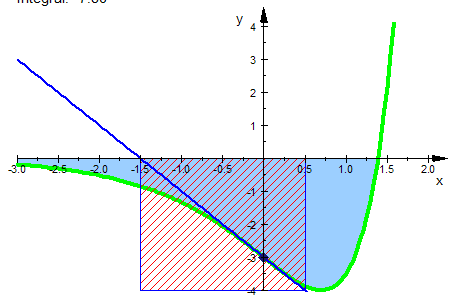
Die blaue Intergralfläche (bis -unendlich) ist stets genauso groß wie der Kasten.
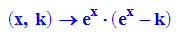
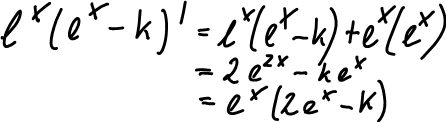
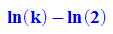
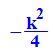
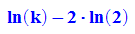
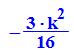
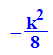
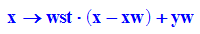
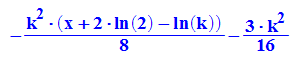
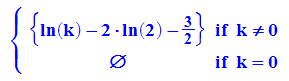
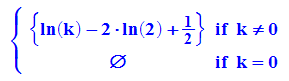
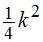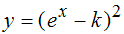
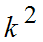