f:=x->x^3-k*x+1
![]()
Kurvendiskussion, die Lerndatei vom Nikolaus
Freiwillige MuPAD-Lernstunde Nikolaustag 2006, Haftendorn und Studis
f:=x->x^3-k*x+1
![]()
So definiert man Funktionen,
Die Zuweisung := muss vorkommen und -> , alles andere ist beliebig.
Sonderzeichen ä,ß....dürfen nicht in Funktonsnamen stehen.
f(x)
![]()
Dieses ist dann der Funktionsterm der Funktion f.
f(3)
![]()
Für x kann man alles einsetzen, wie es die Mathematik erlaubt.
Das gilt auch für ganze Terme:
f(3*k+1)
![]()
Zu der Funktion sind auch die Ableitungen in der üblichen Weise zu haben:
f'(x)
![]()
Da MuPAD ein CAS ist, darf k im Term bleiben
f''(x)
![]()
Die 2. Ableitung enthält kein k mehr.
Da sieht man schon, dass alle Scharkurven eine gemeinsame Wendestelle
bei x=0 haben. (weiter siehe unten)
----------------------------
Nun soll gezeichnet werden. Dazu muss MuPAD wissen, für welches k man
die Kurve sehen will.
Zunächst wählen wir fest:
k:=3:
Mit dem Button von der Komandoleiste erhalten wir den "Schnellzeichner" plotfunc
plotfunc2d(f(x))
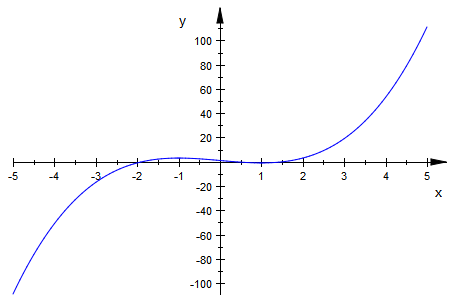
Er stellt von -5 bis +5 alle Werte dar. Das hilft immerhin, einen besseren Zeichenbereich zu überlegen. Dabei erledigen wir auch noch andere sinnvolle Wünsche.
plotfunc2d(f(x),x=-3..3, ViewingBoxYRange=-2..5,
LineWidth=1, GridVisible=TRUE ,
Scaling=Constrained );
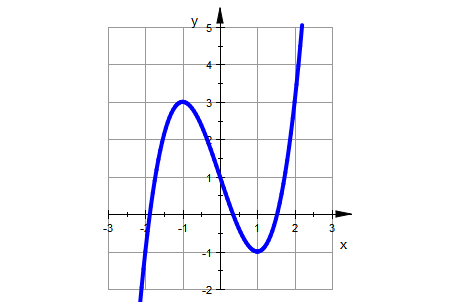
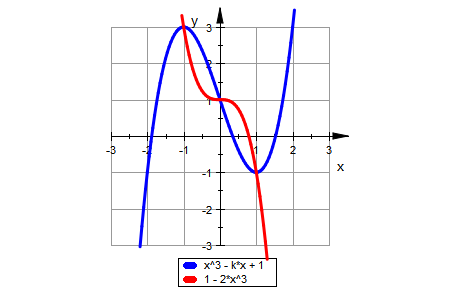
Im Moment ist k=3, wir wollen aber noch andere Scharkurven in demselben Bild sehen. Dazu löschen wir erst den Wert von k wieder. Dann verwenden wir den "mit-Operator", den senkrechten Strich von der Tastatur, und tragen mehrere Funktionen mit Komma getrennt ein.
delete k:
plotfunc2d(f(x)|k=0.5,f(x)|k=1,f(x)|k=2,f(x)|k=3,
x=-3..3,ViewingBoxYRange=-1..3,
LineWidth=1, GridVisible=TRUE ,
Scaling=Constrained );
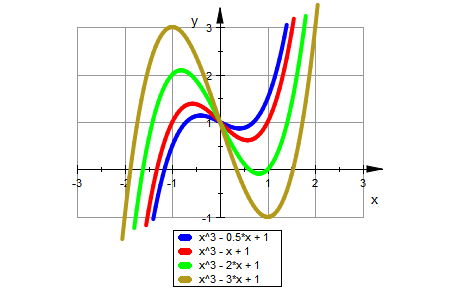
Auf die Idee den YRange anders zu wählen, kann man so kommen:
Klicken in das Bild, oben Zoom, dann ein Fenster aufziehen und ansehen.
Wenn es schön ist, dann die Grenzen für x-und YRange eintragen.
Das Eintragen ist nötig, wenn man bei neuem Auswerten das bessere Fenster
haben will, sonst kommt wieder das alte Fenster.
Wenn wir die Scharkurven ansehen, wird klar, dass für größer werdende k die Extrema weiter nach außen wandern, während alle Graphen durch (0/1) verlaufen.
Das ist dann der gemeinsame Wendepunkt. Es ist tatsächlich:
f(0)
![]()
unabhängig von k. Das beweist die letzte Behautung nun vollständig.
-----------------------------------------------------
Machen wir nun weiter mit der "üblichen" Kurvendiskussion.
Nullstellen:
solve(f(x)=0,x)
![]()
Mit allgemeinem k sind Gleichungen 3. Grades nicht so einfach lösbar.
(Stichwort: Cardanische Formeln siehe www.mathematik-verstehen.de im Bereich
Algebra, Gleichungen)
Im schulischen Rahmen sind die Nullstellen nur mit Einsatz numerischer Verfahren
zu haben. (Newton...) In CAS gibt es das direkt:
numeric::solve(f(x)|k=3,x)
![]()
Das passt zu Zeichnung.
Notwendige Bedingung für Extremstellen:
f'(x);
xe:=solve(f'(x)=0,x)
![]()
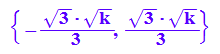
Man sieht, dass es für k>0 geau zwei Extremstellen gibt.
Dass es wirkliche Extremstellen sind, ist klar, da die Parabel f' hier das Vorzeichen wechselt.
(Nach oben geöffnet und Scheitel tiefer als x-Achse für alle k>0)
plotfunc2d(f'(x)|k=3)
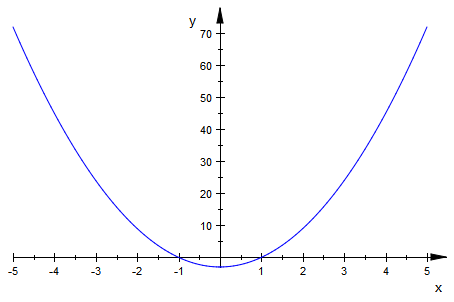
Für k=0 liegt eine doppelte Nullstelle von f' vor, damit also kein
Vorzeichenwechsel von f', also gibt es eine Sattelstelle von f bei x=0 für k=0.
für k<0 haben die Scharkurven keine Extrema.
------------------------------------------------------------------
xe hat in der Ausgabe geschweifte Klammern, ist also eine Menge.
Das i-te Element aus einer Menge (oder Liste) greift man mit Anhängen von [i] heraus.
xe1:=xe[1];
xe2:=xe[2];
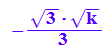
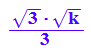
Nun sind die Extemstellen getauft.
Ob es wirkliche Extrema sind, soll bei manchen Lehrern die 2.Ableitung zeigen.
Es ist zwar nicht mehr nötig, aber bitte:
f''(xe1); f''(xe2);
![]()
![]()
Also Extrema nur für k>0
Ordinaten an den Extremstellen
ye:=f(x)$ x in xe
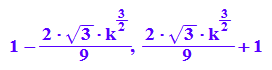
$ ist der Folgenoperator, er ist sehr praktisch und mächtig.
( [x,f(x)]|k=3 ) $ x in xe
![]()
Das sind nun die Extrempunkte für k=3.
Nun z.B. noch die Extrempunkte für k=2
( [x,f(x)]|k=2 ) $ x in xe
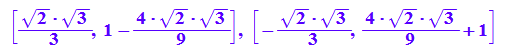
Da ist es sinnvoll, Dezimalzahl-Ausgabe (float) für Alles zu wünschen.
map lässt float auf die vorige Ausgabe, die mit % bezeichnet wird, wirken.
map(%,float)
![]()
Obwohl wir es hier ja schon wissen, dass [0,1] Wendepunkt aller Scharkurven ist, sei berechnet:
notwendige Bedingung für Wendestelle:
f''(x);
solve(f''(x)=0,x)
![]()
![]()
Ordinate
f(0)
![]()
für alle k dieselbe, gemeinsamer Wendepunkt
W:=[0,1]
![]()
Nun soll die Schar nocheinmal animiert dargestellt werden:
plotfunc2d(f(x),x=-3..3,ViewingBoxYRange=-3..3,k=-1..3,
LineWidth=1, GridVisible=TRUE ,
Scaling=Constrained)
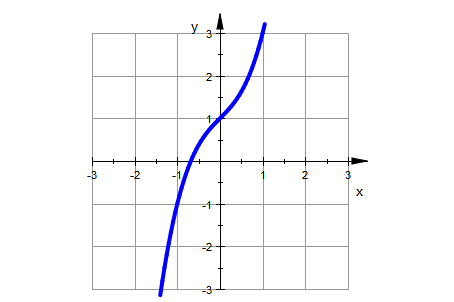

Es ist bei dieser Aufgabe eine schöne Frage:
Auf welcher Kurve liegen eigentlich alle Extrempunkte?
Die koordinaten der Extrempunkte hängen von k ab.
Damit hat man schon eine Parmeterdarstellung der Kurve.
Eine Funktionsdarstellung erhält man, wenn ma k eliminiert.
Man kann auch gleich f'(x)=0 nach k auflösen und das in den Term
von f(x) für k einsetzen
solve(f'(x)=0,k);
k_ex:=%[1]
![]()
![]()
Man sieht, dass k_ex positiv ist, wie wir schon wussten.
g:=x->f(x)|k=k_ex; g(x)
![]()
![]()
Die Kurve der Extrema ist eine verschobene Sattelfunktion.
g(x) in den vorigen Zeichenbefehl einfügen:
plotfunc2d( f(x),g(x),x=-3..3,ViewingBoxYRange=-3..3,k=-1..3,
LineWidth=0.7, GridVisible=TRUE ,
Scaling=Constrained)