f:=x->x*ln(x)
![]()
xlnx-eine interessante Funktion und dazu eine Schar
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Jan. 07 Update Feb.07
Web: www.mathematik-verstehen.de https://mathe.web.leuphana.de
#######################################################################
f:=x->x*ln(x)
![]()
Zeichnung aus Bausteinen
plotfunc2d(x,x*ln(x),ln(x),1,-1,x=0..4, ViewingBoxYRange=-4..4)
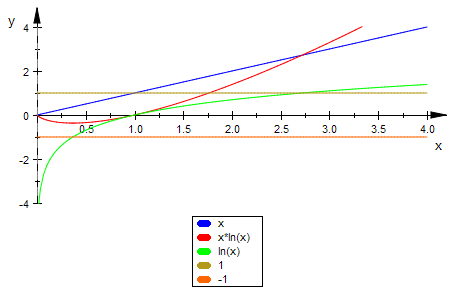
Nullstellen:
Betrachtung von x->0: Die Darstellung zeigt, dass f(0) im Grenzwert 0 sein könnte. Das hieße,
dass die Wh. y=x stärkeren Einfluss hat als der ln. Ohne genauere Untersuchung ergibt sich aber
keine sichere Auskunft über das Verhalten für x->0. Weiteres siehe unten.
Wegen ln(1)=0 (und Wh ungleich 0) ist x=1 Nullstelle von f. Weitere Nullstellen kann es nicht geben,
1-Stellen:
Bei x=1/e: f(1/e)=1/e *(-1)=-1/e negativer Wert im Steifen 0..-1.
bei x=e: f(e)=e*1 Schnitt von f mit Wh.
bei x=1: Es muss sich um eine Berührung von f und ln handeln. Grund:
a)Die Wh ist links von 1 kleiner 1, der ln aber negativ, daher ist f negativ und dichter an der x-Achse als der ln.
b)Die Wh ist rechts von 1 größer 1, der ln aber positiv, und ist f positiv und höher als der ln.
Gesamtverhalten:
Der Definitionsbereich ist Ro+ .
Für große x liegt f zwischen der Parabel y=x 2 und der Wh. y=x
++++++++++++++++++++++++++++++++++++++
Genauere Untersuchung der (einseitigen) Umgebung von x=0.
hold(x*ln(x)=ln(x)/(1/x))
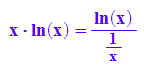
Für diesen Bruch treffen die Voraussetzungen für die Regel von de l'Hospital zu.
limit(ln(x),x=0, Right), limit(1/x,x=0, Right)
![]()
ln'(x), diff((1/x),x)
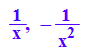
ln'(x)/ diff((1/x),x)
![]()
limit(%,x=0)
![]()
Damit ist der Wert f(0)=0 als Grenzwert gesichert.
f'(x)
![]()
limit(f'(x),x=0,Right)
![]()
Damit geht f mit Steigung minus unendlich in den Ursprung.
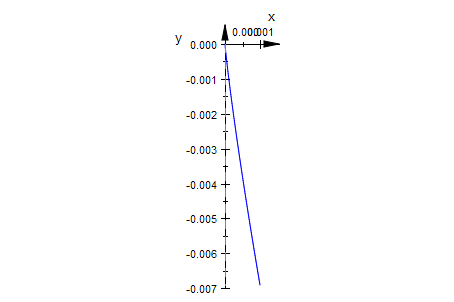
plotfunc2d(f(x),x=0..0.001)
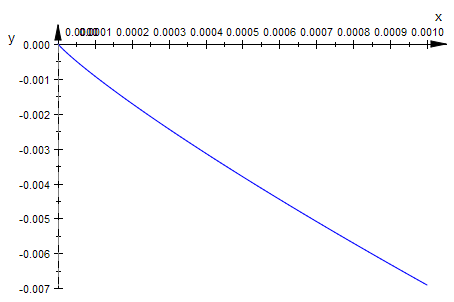
Das sieht oben nicht so aus!!! Aber man muss eben aufpassen und das Seitenverhältnis
gleich machen, wenn man Steigungen beurteilen will.
plotfunc2d(f(x),x=0..0.001, Scaling=Constrained)
dq:=(x,h)->(f(x+h)-f(x))/h; dq(x,h)
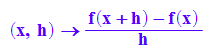
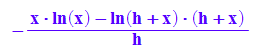
limit(dq(x,h),h=0);
limit(dq(x,h),x=0)
![]()
![]()
Wie mann es auch macht, auch wenn man im Differenzenquotienten erst x gegen Null
streben lässt und dann h, kommt man auf minus unendlich.
#################################################################
Kurvenschar
Die Gerade wird nach rechts verschoben
fa:=x->(x-a)*ln(x);
![]()
plotfunc2d(x-a, (x-a)*ln(x),ln(x),1,x=0..8,a=0..6,
ViewingBoxYRange=-4..3, LineWidth=0.5,
Scaling=Constrained, LegendVisible=FALSE)
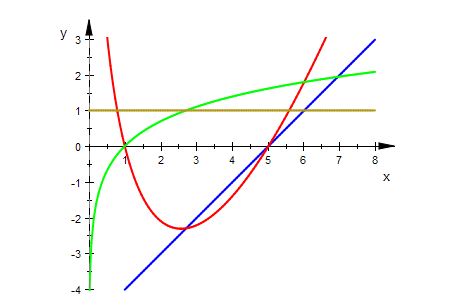

Schlüsse aus der Betrachtung der Bausteine
Die Bausteingerade y=x-a hat stets a als Nullstelle und erzwingt diese Nullstelle auch für fa.
Da gilt sofort für a>0, aber, wie oben zu sehen, auch für a=0.
Für a=0 ist fa=f. (siehe oben).
Für a>0 hat fa an der Stelle x=0 eine Polstelle, sie ist nicht im Definitionsbereich.
Eine weitere Nullstelle von f ist die Nullstelle 1 vom ln.
Zwischen 1 und a muss es ein Extremum von fa geben ( Satz von Rolle).
Für a=1 fallen die beiden Nullstellen zusammen, es gibt eine Berühr-Nullstelle bei x=1,
dieses fa ist die einizige nichtnegative Funktion unter den fa.
Im Punkt (e / e-a) schneidet die Bausteingerade die Kurve fa.
Dieser Punkt wandert beliebig tief, wenn mit wachsendem a die Bausteingerade
nach rechts wandert. Daher erreicht fa im 4. Quadranten alle Punkte mit x>1.
Damit nimmt auch das Extremum beliebig tiefe Werte an.
Ein Wendepunkt scheint nicht zu existieren.
fa''(x)
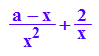
solve(fa''(x)=0,x)

Für positive a und x>0 existiert also wirklich kein WP.
f''(x);
solve(f''(x)=0,x)
![]()
![]()
Für a=0 existiert auch keiner.
+++++++++++++++++++++++++++++++++++++++++++++
plotfunc2d(fa(x),x=0..10,a=0..6, ViewingBoxYRange=-5..15)

Bestimmung des Extremums
fa'(x)
![]()
Also ist das Extremum an der Stelle, wo sich f und die Gerade y=a-x schneiden.
Demontration davon:

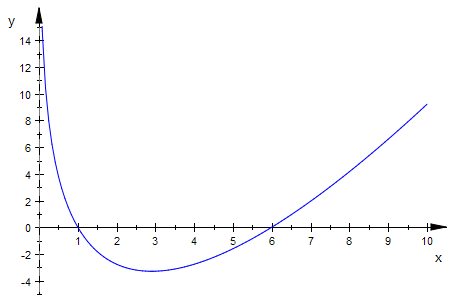
plotfunc2d(-x+a,fa(x),x*ln(x),x=0..10,a=0..6,
ViewingBoxYRange=-4..10)

fag:=plot::Function2d(fa(x),x=0..8,a=0..6,LineColor=[1,0,0],
ViewingBoxYRange=-4..5):
fg:=plot::Function2d(f(x),x=0..8,a=0..6,LineColor=[0,1,0],
ViewingBoxYRange=-4..5):
axg:=plot::Function2d(a-x,x=0..8,a=0..6,LineColor=[0,0,1],
ViewingBoxYRange=-4..5):
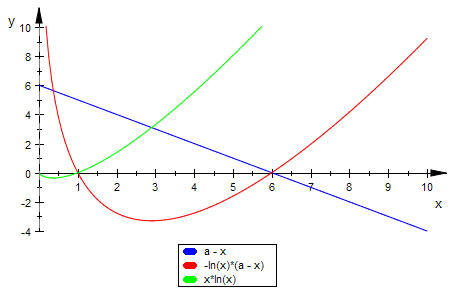
plot(fag,fg,axg, LineWidth=0.5, Scaling=Constrained)

Da die Schnittstellen-Bestimmung (ebenso wie die Extremstellenbestimmung) auf eine
tranzendente Gleichung führen, sind im Folgenden numerische Werte beschafft.
numeric::fsolve(fa'(x)=0,x)$a=0..4 ;
numeric::fsolve(f(x)=a-x,x)$a=0..4 ;
![]()
![]()
Tatsächlich zeigen sich für a>0 dieselben Werte.
Noch für Werte von a zwische 0 und 1:
numeric::fsolve(fa'(x)=0,x)$a=0.1..1 step 0.3;
numeric::fsolve(f(x)=a-x,x)$a=0.1..1 step 0.3;
![]()
![]()
Auch für a=0 schneidet f die Gerade y=a-x an der Extremstelle.
Man musste das numerische Werkzeug genauer steuern.
numeric::fsolve(f(x)=a-x|a=0,x=0.1..0.6);
![]()
Erinnerung, welche Funktionen betrachtet werden.
f(x),fa(x),fa'(x)
![]()
Das folgende Bild zeigt den Zusammenhang nochmals auf andere Art.
plotfunc2d(fa(x),-a+x+f(x)+fa(x),x=0..5,a=0..4,LegendVisible=FALSE,
LineWidth=0.7, Scaling=Constrained,ViewingBoxYRange=-3.5..2)
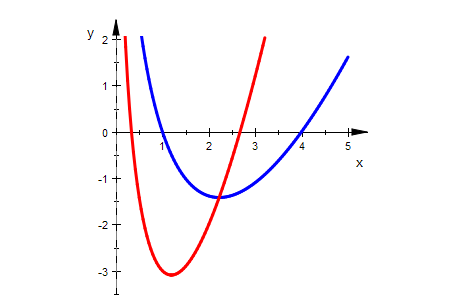

Integrale werden zu aufwändig:
int(-fa(x), x);
int(-fa(x), x=1..a);
%|a=E
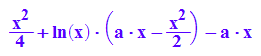
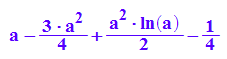
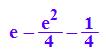
#####################################################
Betrachtung von f(x)=x ln(x)
a) Sei Q=(q,f(q)) ein Punkt des Graphen. Mit zwei Geraden
ergibt sich eine Flächen-Besonderheit:
Gerade durch den Ursprung und f
g:=x->f(q)/q*x; g(x)
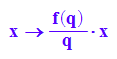
![]()
assume(q>0);
int(g(x)-f(x), x);
int(g(x)-f(x), x=0..q);
![]()
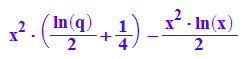
![]()
Tangente in Q an f
t:=x->f'(q)*(x-q)+f(q);simplify( t(x))
![]()
![]()
Fläche zwischen f und dieser Tangente im Bereich 0 bis q
int(f(x)-t(x), x);
int(f(x)-t(x), x=0..q);
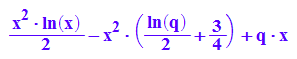
![]()
Erstaunlichererweise ergibt sich hier die gleiche Flächengröße.
Schnitt der Tangente mit der y-Achse
expand(t(0))
![]()
Das ermöglicht eine gute Darstellung diese Flächengröße
fg:=plot::Function2d(f(x),x=0..5,q=0..4, LineColor=[1,0,0]):
tg:=plot::Function2d(t(x),x=0..5,q=0..4, LineColor=[0,0,1]):
gg:=plot::Function2d(g(x),x=0..5,q=0..4, LineColor=[0,1,0]):
polyo:=plot::Polygon2d([[0,-q],[q,0],[q,-q/2]],q=0..4,
FillColor=[0,1,0,1], Filled=TRUE,
FillPattern=HorizontalLines, LineColor=[0,1,0]):
polyu:=plot::Polygon2d([[0,-q],[q,-q],[q,-q/2]],q=0..4,
FillColor=[0,0,1,0.5],FillPattern=VerticalLines,
LineColor=[0,0,1], Filled=TRUE):
li:=plot::Line2d([0,-q],[q,-q/2],q=0..4, LineColor=[1,0,0]):
Q:=plot::Point2d([q,f(q)],q=0..4,PointStyle=Crosses):
plot(tg,gg,fg,Q,polyo,polyu,li,ViewingBoxYRange=-4..7,LineWidth=0.5,
Scaling=Constrained)
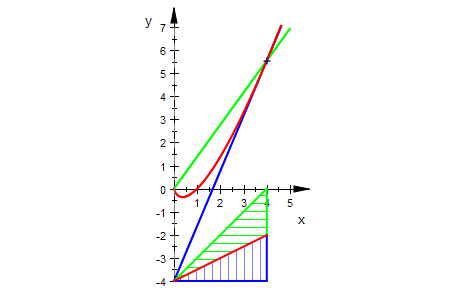

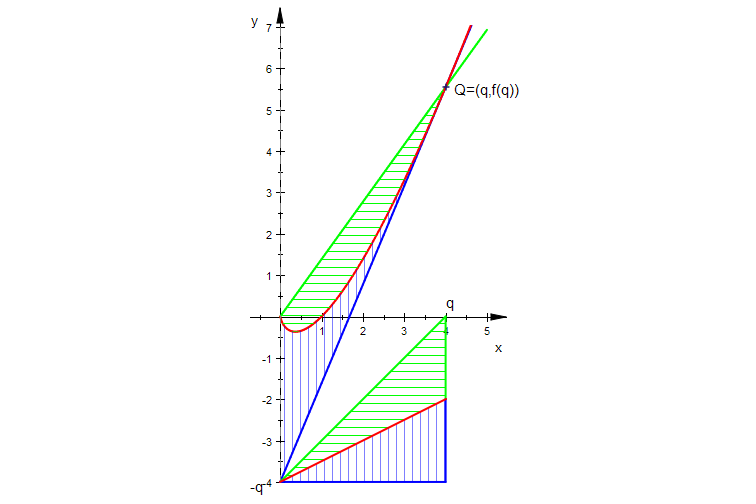
So kann man alle Fälle beobachten.
Die Integrale auch Schraffieren geht nur bei festem q
q:=4:
fg:=plot::Function2d(f(x),x=0..5, LineColor=[1,0,0]):
tg:=plot::Function2d(t(x),x=0..5, LineColor=[0,0,1]):
gg:=plot::Function2d(g(x),x=0..5, LineColor=[0,1,0]):
polyo:=plot::Polygon2d([[0,-q],[q,0],[q,-q/2]],
FillColor=[0,1,0,1], Filled=TRUE,
FillPattern=HorizontalLines, LineColor=[0,1,0]):
polyu:=plot::Polygon2d([[0,-q],[q,-q],[q,-q/2]],
FillColor=[0,0,1,0.5],FillPattern=VerticalLines,
LineColor=[0,0,1], Filled=TRUE):
li:=plot::Line2d([0,-q],[q,-q/2], LineColor=[1,0,0]):
Q:=plot::Point2d([q,f(q)],PointStyle=Crosses):
fqg:=plot::Function2d(f(x),x=0..q, LineColor=[1,0,0]):
tqg:=plot::Function2d(t(x),x=0..q, LineColor=[0,0,1]):
gqg:=plot::Function2d(g(x),x=0..q, LineColor=[0,1,0]):
zwgf:=plot::Hatch(gqg,fqg, FillColor=[0,1,0],
FillPattern=HorizontalLines ):
zwft:=plot::Hatch(fqg,tqg,FillColor=[0,0,1,0.5],
FillPattern=VerticalLines):
Qt:=plot::Text2d("Q=(q,f(q))",[q+0.2,f(q)-0.2]):
qt:=plot::Text2d("q",[q,0.2]):
qy:=plot::Text2d("-q",[-0.73,-q-0.25]):
plot(tg,gg,fg,Q,Qt,qt,qy,polyo,polyu,li,zwgf,zwft,
ViewingBoxYRange=-4..7,LineWidth=0.5,
Scaling=Constrained)
q:=E:
fg:=plot::Function2d(f(x),x=0..3, LineColor=[1,0,0]):
tg:=plot::Function2d(t(x),x=0..3, LineColor=[0,0,1]):
gg:=plot::Function2d(g(x),x=0..3, LineColor=[0,1,0]):
polyo:=plot::Polygon2d([[0,-q],[q,0],[q,-q/2]],
FillColor=[0,1,0,1], Filled=TRUE,
FillPattern=HorizontalLines, LineColor=[0,1,0]):
polyu:=plot::Polygon2d([[0,-q],[q,-q],[q,-q/2]],
FillColor=[0,0,1,0.5],FillPattern=VerticalLines,
LineColor=[0,0,1], Filled=TRUE):
polylio:=plot::Polygon2d([[0,q],[q,q],[0,q/2]],
FillColor=[0.5,0.5,0,1], Filled=TRUE,
FillPattern=CrossedLines, LineColor=[0.5,0.5,0]):
polyliu:=plot::Polygon2d([[0,q/2],[0,0],[q,q]],
FillColor=[1,0,1,1],FillPattern=DiagonalLines,
LineColor=[1,0,1], Filled=TRUE):
li:=plot::Line2d([0,-q],[q,-q/2], LineColor=[1,0,0]):
Q:=plot::Point2d([q,f(q)],PointStyle=Crosses):
fqg:=plot::Function2d(f(x),x=0..q, LineColor=[1,0,0]):
tqg:=plot::Function2d(t(x),x=0..q, LineColor=[0,0,1]):
gqg:=plot::Function2d(g(x),x=0..q, LineColor=[0,1,0]):
zwgf:=plot::Hatch(gqg,fqg, FillColor=[0,1,0],
FillPattern=HorizontalLines ):
zwft:=plot::Hatch(fqg,tqg,FillColor=[0,0,1],
FillPattern=VerticalLines):
Qt:=plot::Text2d("E=(e,e)",[q+0.2,f(q)-0.2]):
qt:=plot::Text2d("e",[q,0.2]):
qy:=plot::Text2d("-e",[-0.7,-q-0.2]):
plot(tg,gg,fg,Q,Qt,qt,qy,polyo,polyu,polylio,polyliu,li,zwgf,zwft,
ViewingBoxYRange=-3..3.1,LineWidth=0.5,
Scaling=Constrained)
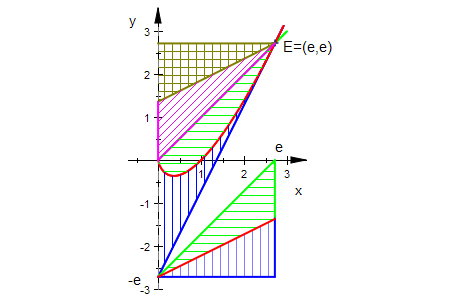
Hier sind alle Flächen gleich groß, dies ist ein Sonderfall des vorigen Erkenntnis.
f(x),f'(x),f''(x)
![]()
Die zweite Ableitung ist für x>0 stets größer als 0, daher kann f keine Wendepunkte haben.
x=0 als Rand des Def.-Bereiches braucht nicht betrachtet zu werden.
###########################################
Krümmung von f in Nähe von x=0:
kappa:=x->f''(x)/(1+f'(x)^2)^(3/2); kappa(x)
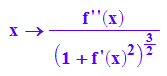
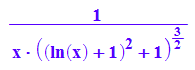
kappa2:=x->1/(x*(1+f'(x)^2)^(3/2)); kappa2(x)
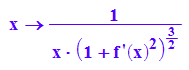
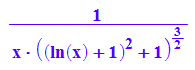
Aus unklaren Gründen, die bei MuPAD nachgefragt habe, verhält sich kappa2 besser als kappa
float(kappa2(x/1000)) $ x=1..60 step 10
![]()
kappa2(0.00001)
![]()
plotfunc2d(kappa(x),kappa2(x), f(x)+1.7,x=0..0.5,
ViewingBoxYRange=1.3..3.3, Scaling=Constrained)
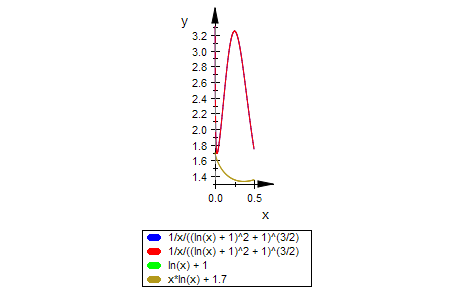
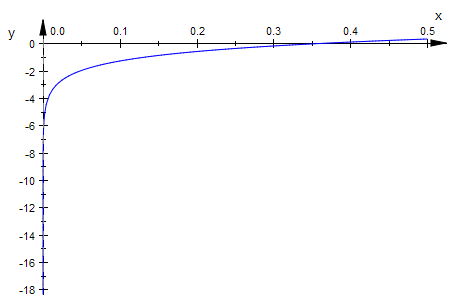
Erstaunlich ist diefür x->0 unendliche Krümmung.
Das passt immerhin zu der drastischen Zunahme des Betrags der Steigung für x gegen 0.
plotfunc2d(f'(x),x=0..0.5)
Krümmungsbetrachtung für a>0
fa(x),fa'(x),fa''(x)
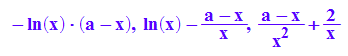
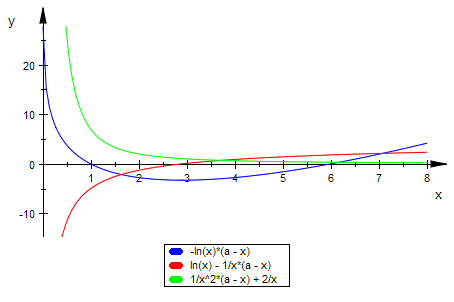
plotfunc2d(fa(x),fa'(x),fa''(x),x=0.01..8,a=0..6)
factor(fa''(x))
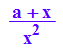
Für positive a kann f'' nur für negative x Null werden und die gehören nicht zum Definitionsbereich.
Also hat auch keins der fa einen Wendepunkt.
a=0 ist oben betrachtet.
kappaa:=x->(a+x)/(x^2*(1+fa'(x)^2)^(3/2)); kappaa(x)
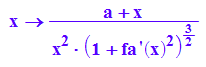
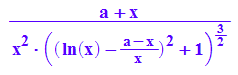
plotfunc2d(kappaa(x), kappaa(x)|a=1,x=0..2,a=0..2, ViewingBoxYRange=0..3.3)
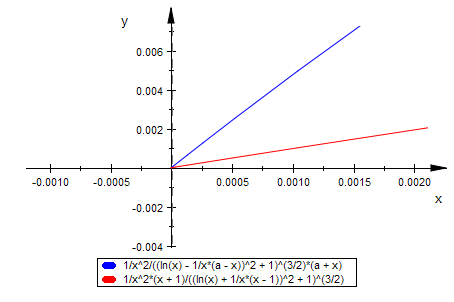
Die Krümmung geht für a>0
plotfunc2d(kappaa(x)|a=0.01,x=0..0.1)
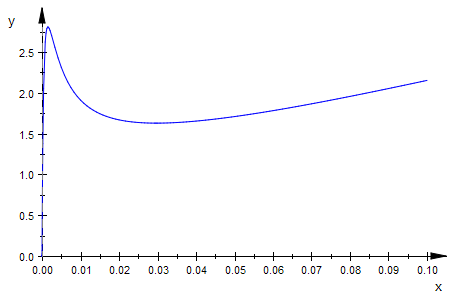
plotfunc2d(kappaa(x)|a=0.01, fa(x)|a=0.01,x=0..1)
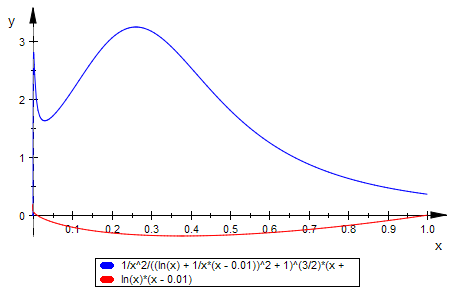
Es ist sehr spannend, welche merkwürdigen Formen die Krümmung annimmt.
Für eine Klausur wird das aber zu schwierig.
#########################################################
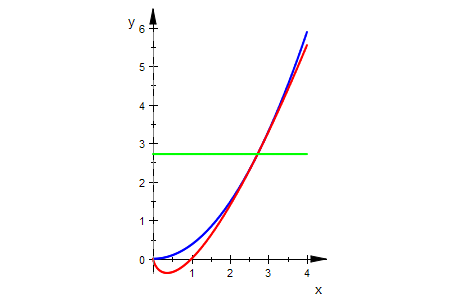
Betrachtung mit einer Parabel
p:=x->1/E*x^2; p(x)
![]()
![]()
plotfunc2d(p(x),f(x),E,x=0..4,LineWidth=0.5,
LegendVisible=FALSE,Scaling=Constrained)
int(p(x)-f(x), x);
int(p(x)-f(x), x=0..E)
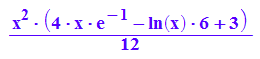
![]()
fa''(2.22341)|a=4
![]()
fa'''(-4)|a=4
![]()
solve(fa''(x)=0,x)
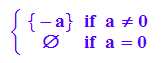
int(x-ln(x), x=0..1);
int(ln(x), x)
![]()
![]()
plotfunc2d(x^2*E,fa(x)|a=4)
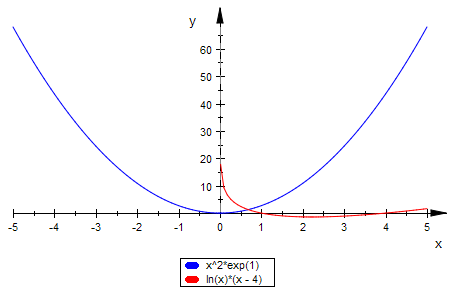
numeric::solve(x^2*E=fa(x)|a=4,x=0.1..1)
![]()