Differentialgleichungen
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, ursprünglich 09.10.01 überarbeitet Sept. 05
Es fehlen nocht textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

dgl:=ode(y'(x)-2*y(x)=sin(x),y(x));//DGL eintragen
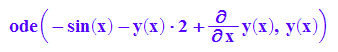
solve(dgl)
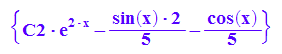
yallg:=op(solve(dgl));
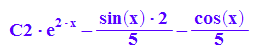
yy:=x->yallg: yy(1) //Funktion daraus machen:Dieses gelingt nicht.
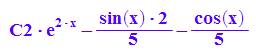
yloesAllg:=xx->yallg|x=xx: //Ohne diesen Klimmzug ging es nicht.
yloesAllg(x)
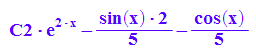
yloesAllg(PI)
![]()
ode heißt ordinary differential equation, gewöhnliche Differentialgleichung, als Argument hat ode die eigentliche
Gleichung und die Funktion, die gesucht ist. solve kann die so gegebene Differentialgleichung allgemein lösen.
Anfangswertproblem
x0Wert:=-1:y0Wert:=0://AWP eintragen, x0, x0 sollen freie Variable bleiben
dglAWP:=ode({y(x0Wert)=y0Wert, y'(x)-2*y(x)=sin(x) },y(x));//DGL eintragen
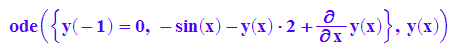
loes:=xx->op(solve(dglAWP))|x=xx:
loes(x);simplify(loes(x)); float(simplify(loes(x)));
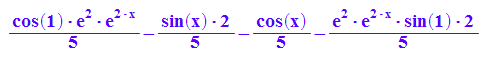
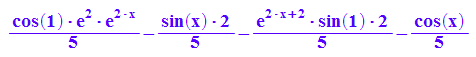
![]()
Proben für diese Lösung:
loes'(x)-2*loes(x) //linke Seite der DGL eintragen, rechts muss dann kommen
![]()
loes(x0Wert)=y0Wert; float(loes(x0Wert))=y0Wert
![]()
![]()
Zeichnen des Richtungsfeldes von DGLn 1. Ordnung,
die man nach y' auflösen kann
g:=(x,y)->(2*y+sin(x)):g(x,y);//DGL eintragen!!!!!!!
![]()
xmin:=-6:xmax:=1:ymin:=-4:ymax:=2://Fenster eintragen !!!!!!!!!!!!
loesGraph:=plot::Function2d(loes(x),x=xmin..xmax,ViewingBoxYRange=ymin..ymax,
Color=RGB::Green):
DIGITS:=5:
field:= plot::VectorField2d( [1,g(x,y)], x=xmin..xmax,y=ymin..ymax,
Color = RGB::Red, ArrowLength=Fixed)://Die 1 musss sein!!!!!!
plot(field,loesGraph, Scaling = Constrained)
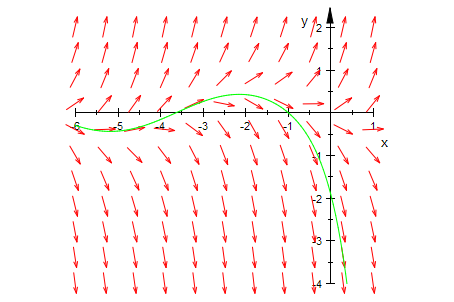
Numerische Lösung entsprechend der Vorlesung Ha
Heunverfahren
heun:=proc(x0,y0) local x00,y00,m0,mz,z,mm,x1,y1;
begin
x00:=float(x0):y00:=float(y0):
x1:=x00+h: m0:=g(x00,y00):z:=y00+m0*h:
mz:=g(x1,z):mm:=(m0+mz)/2:y1:=y00+mm*h:
return(x1,y1)
end_proc:
heunPrint:=proc(x0,y0,h) local x00,y00,m0,mz,z,mm,x1,y1;
begin
x00:=float(x0):y00:=float(y0):
x1:=x00+h: m0:=g(x00,y00):z:=y00+m0*h:
mz:=g(x1,z):mm:=(m0+mz)/2:y1:=y00+mm*h:
DIGITS:=8;
[[x00,y00],h,m0,z,mz,mm,[x1,y1]];
end_proc:
h:=0.2:heun(x0Wert,x0Wert)// Schrittweite wählen
![]()
heunPrint(x0Wert,y0Wert,h)
![]()
Hier stehen [x0,y0],h,m0,z,mz,mm,[x1,y1]
heun(heun(x0Wert,y0Wert)) //Ein nächster Schritt
![]()
heunPrint(heun(x0Wert,y0Wert),h)
![]()
n:=6:liste:=(heun@@i)(x0Wert,y0Wert) $ i=1..n://Folge xi,yi
punkte:=[liste[j],liste[j+1]]$ j=1..2*n-1://Kombination zu Punkten
punkte:=punkte[2*j-1] $ j=1..n //Folge der Heunpunkte
![]()
punkte:=[x0Wert,y0Wert],punkte; //Davor der Start zugefügt
![]()
heunpkte:=plot::Listplot([punkte],PointSize=2,Color=RGB::Green):
plot(field,heunpkte)
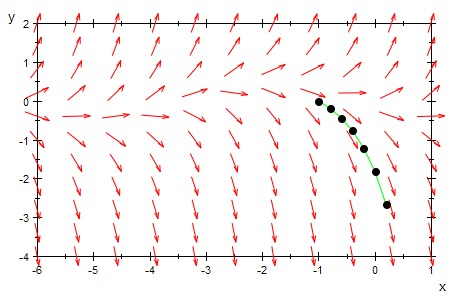
plot(field,heunpkte,loesGraph,Axes=Origin,
TicksDistance = 2.0, GridVisible = TRUE,
SubgridVisible = TRUE,Scaling=Constrained)
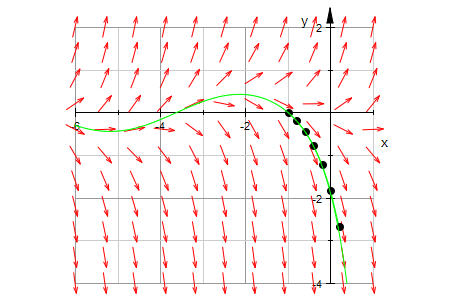
Die exakte Lösung stimmt mit der numerischen Lösung und dem Richtungsfeld gut überein.
Numerische Lösung mit MuPAD
Frage, welche Syntax odesolve hat und wie man DGLn zeichnet
h:=0.2: n:=6: //Wie oben
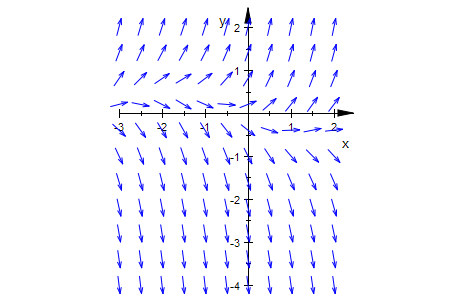
Feld := plot::VectorField2d([1, g(x, y)], x = -3..2, y = -4..2,
Color = RGB::Blue, ArrowLength=Fixed):plot(Feld, Scaling=Constrained)
//Feld hat nur etwas andere Maße als field
x0Wert;y0Wert;//zur Erinnerung
![]()
![]()
Hier muss man nochmal die DGL eintragen, denn in g(x,y) ist y nur als Variable.
Mit dem folgenden Befehl werden G, X0 und Y0 belegt.
[G,X0, Y0] := [numeric::ode2vectorfield(
{y'(x) = 2*y(x)+sin(x) , y(x0Wert) =y0Wert}, [y(x)])]
![]()
X0
![]()
Erzeugung der Werte mit numeric::odesolve
MuPkte:=[x0Wert+i*h,
op(numeric::odesolve(
G, X0..x0Wert+i*h, [0],Stepsize=h, RK4))]$i=1..n:
Stepsize=h, RK4))]$i=1..n:
Wichtig ist, dass man mit RK4 das Rung-Kutta-Verfahren 4.Ordnung wählt.
Alternative ist u.a. Euler1
MuPkte:=[x0Wert,y0Wert],MuPkte
![]()
MuPkteGraph:=plot::Listplot([MuPkte],
PointSize=3,PointStyle=Stars,Color=RGB::Magenta):
plot(Feld,MuPkteGraph,heunpkte, Axes=Origin, TicksDistance = 1, GridVisible = TRUE,
SubgridVisible = TRUE,Scaling=Constrained):
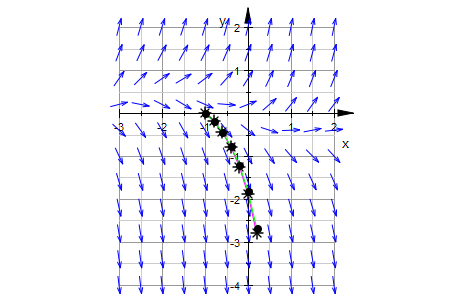
Man sieht, dass die Runge-Kutta-Punkte und die Heun-Punkte
fast aufeinander liegen.
g(x,y);x0Wert;y0Wert;h; //zur Erinnerung
![]()
![]()
![]()
![]()
[G,X0, Y0] ist oben schon erzeugt
Hier wird nun die numerische Lösung direkt von Mupad gezeichnet.
p1 := plot::Ode2d(G, [-1+i*h $ i=0..6], Y0,RK4,Stepsize=h,
PointSize = 2*unit::mm,
PointStyle = FilledCircles):
p2:= plot::Ode2d(G, [-4+i*h $ i=0..6], Y0,RK4,Stepsize=h,
PointSize = 2*unit::mm,
PointStyle = FilledDiamonds):
p3:= plot::Ode2d(G, [-4+i*h $ i=0..6], [-1],RK4,Stepsize=h,
PointSize = 2*unit::mm,
PointStyle = FilledDiamonds):
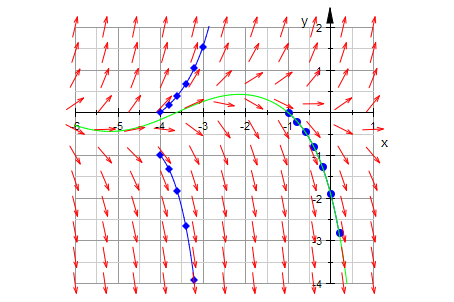
plot(p1,p2,p3,loesGraph,field ,TicksDistance = 1, GridVisible = TRUE,
SubgridVisible = TRUE,Scaling=Constrained):
all:=plot::Ode2d(G, [-6+i*h $ i=0..16], [-1+k*0.1],RK4,Stepsize=h,
PointsVisible =FALSE)$ k=0..10:
all2:=plot::Ode2d(G, [-1+i*h $ i=0..16], [-2+k*0.5],RK4,Stepsize=h,
PointsVisible =FALSE)$ k=0..10:
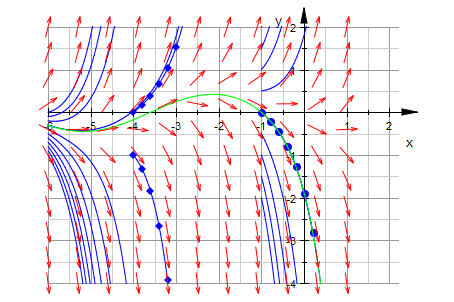
plot(all,all2,p1,p2,p3,loesGraph,field ,TicksDistance = 1, GridVisible = TRUE,
SubgridVisible = TRUE,Scaling=Constrained)
Isoklinen
iso:=(x,m)->op(solve(m=g(x,y),y)):iso(x,m);
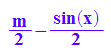
alleIso:= iso(x,m/4) $ m=-8..8//Achtung, Bereich anpassen
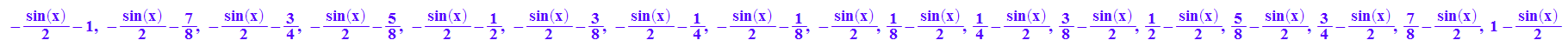
plotfunc2d(alleIso)
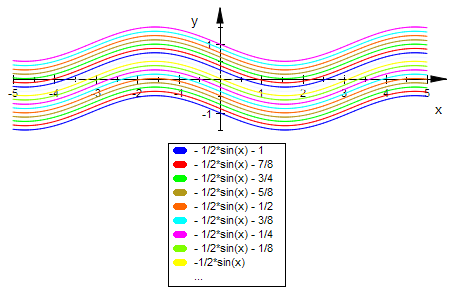
Man sieht hier deutlich, dass nur in einem schmalen Bereich um die x-Achse herum flache
Steigungen vorkommen können. In diesem Bereich entscheidet sich durch kleinste Änderungen
in den Anfangswerten, ob die Lösungsfunktion nach oben oder nach unten geht.
alleIso:=plot::Function2d(iso(x,m/2),x=-6..xmax,
Color=RGB::Green ) $ m=-8..8:
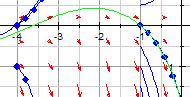
plot(alleIso,field,Scaling = Constrained)
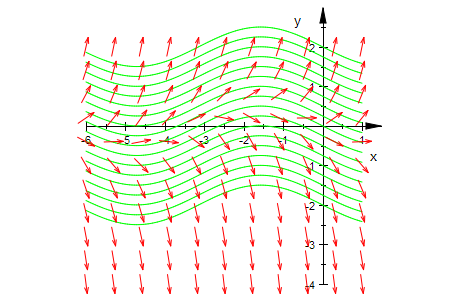
In diesem Bereich entscheidet sich durch kleinste Änderungen
in den Anfangswerten, ob die Lösungsfunktion nach oben oder nach unten geht.