saiteDGL:=y->diff(y(x,t), t,t)=`α`^2*diff(y(x,t), x,x)
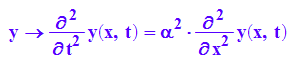
Riemann und die Wellengleichung
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Sept 07 Update 21.09.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de ######################################################
Dateiname riemann-trig.mn
saiteDGL:=y->diff(y(x,t), t,t)=`α`^2*diff(y(x,t), x,x)
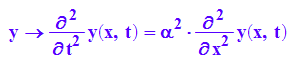
Differentialgleichung einer schwingenden Saite
f:=(x,t)->sin(k*PI*x)*cos(k*PI*`α`*(t-`β`));
![]()
diff(f(x,t),t,t);
diff(f(x,t),x,x);
![]()
![]()
saiteDGL(f)
![]()
Linke Seite = rechte Seite Also ist f ein Lösung der DGL
Wenn k ganze Zahl ist, sind die Randbedingungen bei einer Saitenlänge von 1 von allein erfüllt.
Die Anfangsbedingung: für t=0 ist die Saite straff:
f(0,t),f(1,t),f(x,0)
![]()
Damit die letzte Bedingung für alle x Null wird, muss der Kosinus 0 werden
solve(`α`*`β`*k=1/2,`β`)
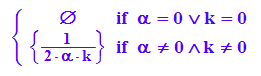
expand(cos(r-s))
![]()
f(x,t)|`&beta`=1/(2*`α`*k)
![]()
expand(cos((hold(k*PI*`α`*t))-PI/2));
![]()
f:=x->sin(k*PI*x)*sin(k*PI*`α`*t)
![]()
k:=3:
plotfunc3d(f(x,t),x=0..1,`α`=0..1,t=0..2*PI);
f(x,t)
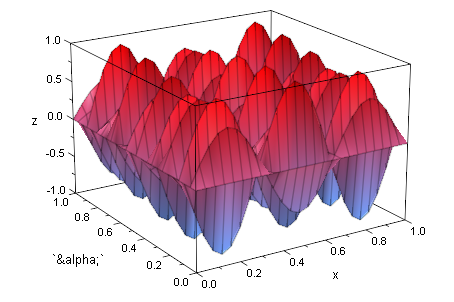
![]()

plotfunc2d(f(x,t)|`α`=1,x=0..1,t=0..60*PI)
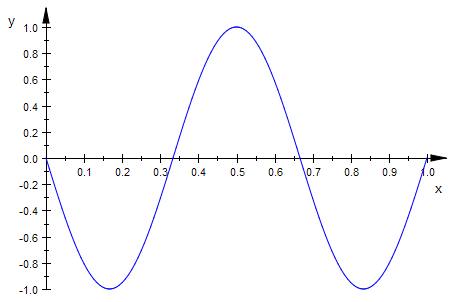
delete k:

##################################################
Addition dieser Funktionen , 6 Summanden, dem 1. ein 4-faches Gewicht gegeben
trigS:=4*(f(x,t)|k=1)+ (f(x,t)|k=2)+(f(x,t)|k=3)+
(f(x,t)|k=4)+ (f(x,t)|k=5)+(f(x,t)|k=6):
`α`:=1:
plotfunc2d(trigS,x=0..8,t=0..8*PI)
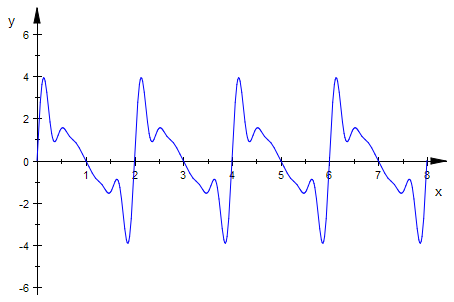

`α`:=1:
plotfunc2d(trigS,x=0..1,t=0..2*PI)
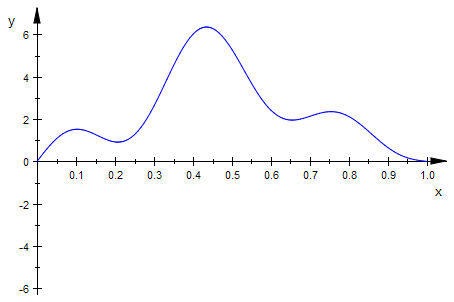

plotfunc3d(trigS,x=0..1,t=0..2*PI)
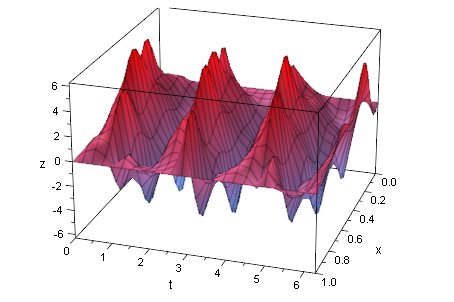
################################################