f:=x->x^3 - x+3
![]()
Kurvendiskussion
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Update Jan 08
https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
________________________________________________________________________________
Autoren:(ehem) Studentinnen: Sandra Gorgas, Maike Mecklenburg,MuPAD 2.5
umgeschrieben auf MuPAD 4 von Haftendorn
Funktionen: plotfunc2d, f',f'', discont, GridVisible, solve, limit
________________________________________________________________________________
Definieren sie die Funktion:
f:=x->x^3 - x+3
![]()
:= bennent den rechten Teil mit Namen hier: f. Der Name darf nicht f(x) lauten, da es Probleme
mit der Zuordnung gibt.
x-> kennzeichnet es als Funktion von x. Nur dann ist später Ableitung bilden mit f' möglich.
1. Skizze des Graphen
plotfunc2d(f(x))
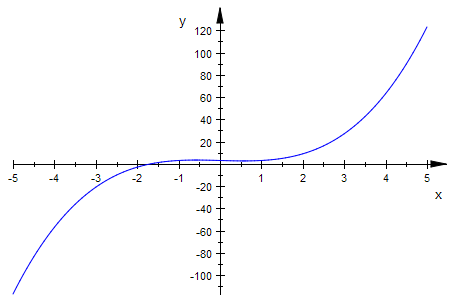
Das sieht nun so aus, als habe f einen Sattel. Am Funktionsterm kann man aber sehen,
dass das nicht stimmen kann. Man denkt sich f aus zwei Bausteinen aufgebaut:
1.) den durch x^3 erzeugten Sattel
2.) die fallende Gerade y= - x+3
dann die Sattelfunktion aufsetzt auf die Gerade. y-Bereich drastisch eingrenzt.
plotfunc2d(f(x),-x+3,x^3, ViewingBox=[-3..3,-5..10])
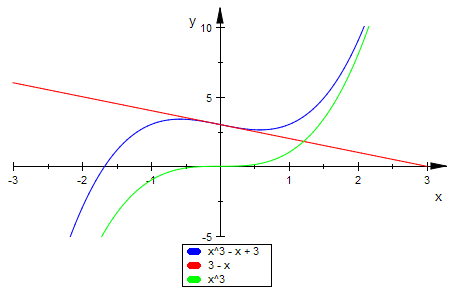
Unstetigkeit kann es bei einem Polynom nicht geben, für alle Fälle aber:
2. Unstetigkeitsstellen
Problemstellen:=discont(f(x),x)
![]()
das x (hinten in der Klammer) bedeutet, dass es nach x berechnet werden soll
-------------------------------
Der Definitionsberech ist bei Polynomen immer ganz R, aber:
3. Definitionsbereich, eher bei gebrochen-rationalen Funktionen
sinnvoll daher hier für den Kehrwert durchgeführt:
discont(1/f(x),x)
![]()
Hier zu sehen, dass die Nullstellen von f die Polstellen von 1/f sind. Klar.
4. y-Achsenabschnitt
f(0)
![]()
5. Nullstellenberechnung
nst:=numeric::solve(f(x)=0,x)
![]()
solve(f(x)=0,x)
![]()
solve ist ein exakter Gleichungslöser. Der erledigt dieses Problem nicht.
Sie Extra-Seiten bei Agebra zu Gleichungen, besonders zu Cardanischen Folmeln.
Daher nuss der numerische Gleichungslöser genommen werden.
Dabei werden auch die komplexen Lösungen angezeigt.
Alle komplexen Zahlen erkennt man am i.
hier: nur eine reelle Lösung -2,08674534.
Man konnte ja schon mit Sicherheit am Graphen sehen, dass es nur eine einfache reelle
Nullstelle gibt. Die greift man so heraus:
x0:=nst[1]; f(x0);
![]()
![]()
6. Ableitungen bilden auf mehrere Arten
Abl1:=diff(f(x),x);
f'(x);
ff:=D(f); ff(x)
![]()
![]()
![]()
![]()
Nun dort einen Wert einsetzen:
subs(Abl1, x = 3)
![]()
f'(3);ff(3)
![]()
![]()
Abl1 ist nur ein Term. In den muss man mit subs(term, x=zahl) einsetzen.
f' ist eine Funktion von x, wie es sich gehört. Darum kann man f'(zahl) bilden.
Mit der Version ff ist hier gezeigt, wie man selbst eine Funktion aus einer
Ableitung machen kann.
------------------------
Zweite Ableitung:
f''(x);
Abl2:=diff(diff(f(x),x),x);
fg:=diff(f'(x),x);
fff:=D(ff);
![]()
![]()
![]()
![]()
Mit der Version fff ist hier gezeigt, wie man selbst eine Funktion aus einer
Ableitung machen kann.
f''(3);
fff(3)
![]()
![]()
fff'(x);
f'''(x)
![]()
![]()
Es gibt 3 Möglichkeiten Ableitungen zu bilden. 1. mit f'(x) oder 2. mif D(f) und 3. mit diff(f(x),x).
Dabei funktioniert der einfache Strich nur für Funktionen von einer Variablen.
Parameter dürfen dabei sein, sofern sie nicht im Funktionsaufruf vorkommen.
Die Version immer nur mit Termen zu arbeiten -wie hier Abl1...- ist nicht so gut,
da man Einsetzungen dann nur mit subs(...) vornehmen kann.
7. Extrema bestimmen
Ext:=solve(f'(x)=0,x)
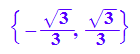
Wende:=solve(f''(x)=0,x)
![]()
8. Prüfung der Extrema
Diese Prüfung ist unsinnig, da Polynome 3.Grades nur dann eine Sattel haben können,
wenn die beiden Nullstellen von f' zusammenfallen. Existieren zwei verschieden Nullstellen von f'
beim Polynom 3. Grades, dann müssen es wirkliche Extremstellen sein.
f''(xe) $ xe in Ext;
![]()
[xe,f(xe)] $ xe in Ext;
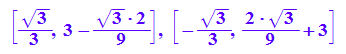
map(%,float)
![]()
Hier stehen nun die Extrema.
f'''(xw) $ xw in Wende
![]()
[xw,f(xw)] $ xw in Wende;
![]()
Dieses ist der Wendepunkt.
Eine Prüfung wäre unsinnig, da Polynome 3.Grades mit 2 Extrema einen
Wendepunkt haben müssen.
Man beachte, dass man die Funktionen nicht auf Mengen anwenden kann.
Das kann man beim TI-voyage, in Mathematica und einigen Systemen.
Man hilft sich mit "$ x in Menge" wie oben oder mit map(menge, fktname)
map(Ext,f)
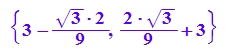
Manchmal ist bei Kurvendiskussionen die Bestimmung einer Asymptote verlangt.
9. Waagerechte Asymptote bestimmen für Kehrwert-Funktion
limit(1/f(x),x=-infinity), limit(1/f(x),x=infinity)
![]()
Schräge Asymptoten können so nicht bestimmt werden
Da muss man die Asymptote raten oder mit einem passenden Verfahren
bestimmen und dann abziehen.
10. Exakte Zeichnung des Graphen
plotfunc2d(x^3-x+3,x=-3..3,YRange=-1..5
,GridVisible=TRUE,Scaling=Constrained)
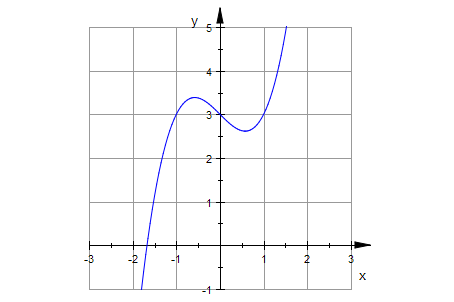
Mit Scaling=Constrained sorgt man für gleichen Maßstab in x und y.