f:=(x,k)->x^2*(x-k)*(x-2)
![]()
Kurvenschar-Diskussion
Analysis mit MuPAD 4, mit Kurven der Extrema und der Wendepunkte
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Okt. 05 Version vom Jul.06 update Aug06
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
f:=(x,k)->x^2*(x-k)*(x-2)
![]()
fani:=plot::Function2d(f(x,k),x=-2..3,k=-1..3,
ViewingBoxYRange=-3..3, Color=RGB::Red, LineWidth=1):
plot(fani);
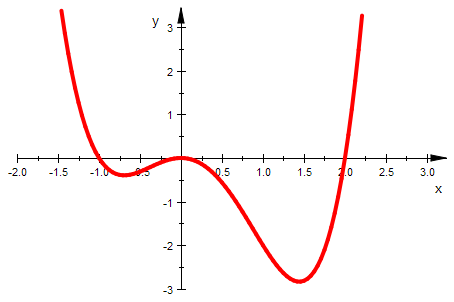

Die Animation geht auch mit dem einfachen plotfunc2d. Hier soll aber später die Kurve
der Extrema hinzugefügt werden. Daher braucht man Graphik-Primitive, wie man sie durch
plot::xxxxxxxx erhält. Die werden dann von plot(...) dargestellt.
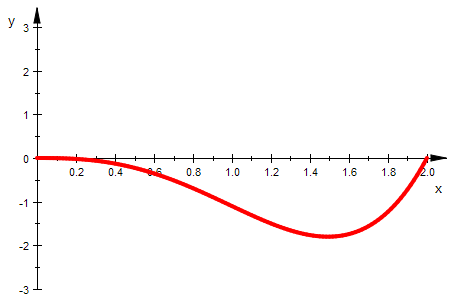
fanika:=plot::Function2d(f(x,k),x=0..2,k=-1..3,
ViewingBoxYRange=-3..3, Color=RGB::Red, LineWidth=1):
plot(fanika);

alle:=f(x,k) $ k=-1..3
![]()
plotfunc2d(alle,x=-1.2..3,YRange=-3..3,
GridVisible=TRUE)
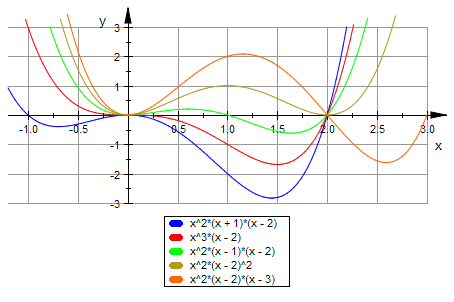
Die Nullstellen sind hier offensichtlich: Gemeinsame doppelte Nullstelle x=0, Berührung,
Gemeinsame Nullestelle bei x=2, weitere Nullstalle bei x=k.
Für k=2 ist auch diese Nullstelle doppelt, also Berührung, sonst ist sie einfach.
für k=0 ist die bei x=0 dreifach, also Sattel, sonst sind alle anderen Nullstellen einfach.
Automatische Bestimmung der Nullstellen:
nst=solve(f(x,k)=0,x)
![]()
Die Vielfachheiten sind nicht zu sehen. Die Klammerform ist aussagekräftiger.
solve(f(x,k)=0,x, Multiple)
![]()
Multiple gibt die Vielfachheit mit aus.
ausmulti:=expand(f(x,k))
![]()
Wenn nun diese Form gegeben wäre, könnte man die Klammerform herstellen.
factor(ausmulti)
![]()
Ableitung und zugehörige Rechnungen
f
![]()
ableit:=diff(f(x,k),x)
![]()
simplify(ableit)
![]()
ableit:=factor(%)
![]()
plotfunc2d(subs(ableit, k=2),x=-3..3,YRange=-3..3)
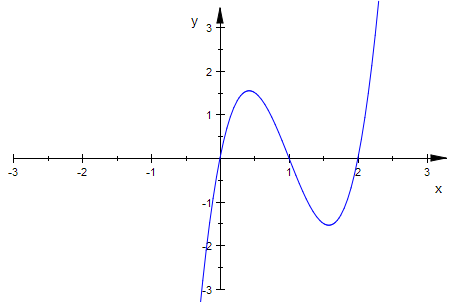
plotfunc2d(subs(ableit),x=-3..3,k=-2..2,YRange=-3..3)
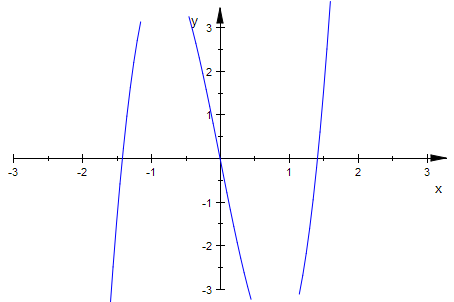
subs(ableit, k=2)
![]()
ableit
![]()
xe:=solve(ableit=0,x)
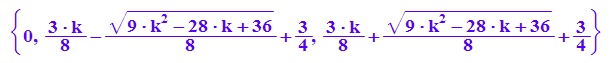
extremstellen:=float(xe) $ k=-1..2
![]()
Achtung, bei Mengen wird die Reihenfolge nicht beibehalten.
ExtremPunkte für k=2:
[xex,f(xex,2)] $ xex in subs(xe,k=2);
![]()
f(x,2)
![]()
Diese Schar-Funktion hat also, wie man gleich sieht, zwei doppelte Nullstellen
und in der Mitte dazwischen ein Maximum.
[xex,f(xex,i)] $ xex in subs(xe,k=i) $ i=-1..3:
matrix([map(%,float)]);

solve(9*k^2-28*k+36=0,k)
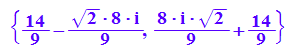
Die Diskriminate wird nie Null, damit existieren i.a. drei Extrempounkte.
Kurve der Extrema
lo:=solve(ableit=0,k)
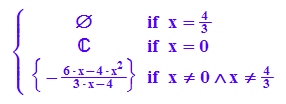
Die Gleichung Ableitung=0 ist nach k aufzulösen.
Von diesen ist die mittlere die gesuchte.
kk:=lo[3][1]
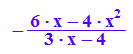
Dieser Term ist für k in f(x,k) einzusetzen
kurveextrema:=subs(f(x,k),k=kk)
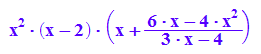
factor(kurveextrema)
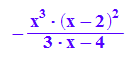
Dieses ist der Funktionsterm der Kurve der Extrema.
Man sieht einen Sattel bei 0, einen Pol bei x=4/3 und eine doppelte Nullstelle bei 2.
plotfunc2d(alle,kurveextrema,x=-1.2..3,YRange=-3..3,
GridVisible=TRUE, LineWidth=0.8)
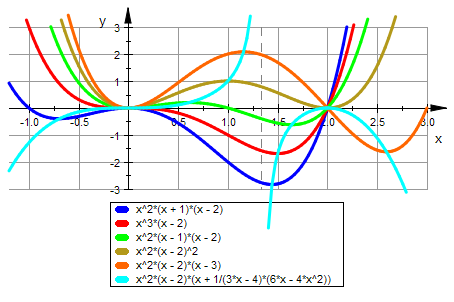
Hier sieht man, dass die Kurve der Extrem (hier blau) gut passt.
Wendepunkte
zw_abl:=diff(ableit,x)
![]()
simplify(zw_abl)
![]()
solve(zw_abl=0,x)
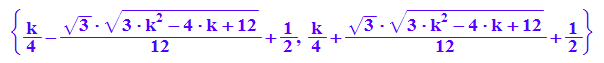
Das sind unangenehme Terme.
solve(3*k^2-4*k+12=0,k)
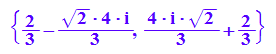
Die Diskriminante wird aber nie Null, damit exitieren
stets zwei Wendepunkte.
wp:=solve(zw_abl=0,k)
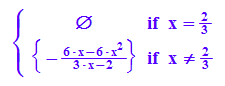
wwp:=wp[2][1]
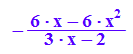
kurvewend:=subs(f(x,k),k=wwp)
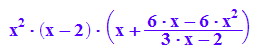
factor(kurvewend)
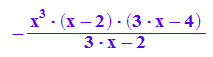
Auch die Kurve der Wendepunkte hat einen Sattel im Ursprung.
Sie hat einen Pol bei x=2/3 und einfache Nullstellen bei x=4/3 und x=2.
Bemerkenswert ist, dass das Intervall [0,2] von diesen beiden
Polstellen genau gedrittelt wird.
plotfunc2d(alle,kurveextrema,kurvewend,x=-1.2..3,YRange=-3..3,
GridVisible=TRUE, LineWidth=0.8)
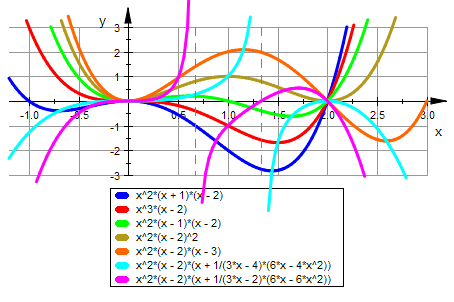
Auch die Kurve der Wendpunkte (hier lila) passt gut.
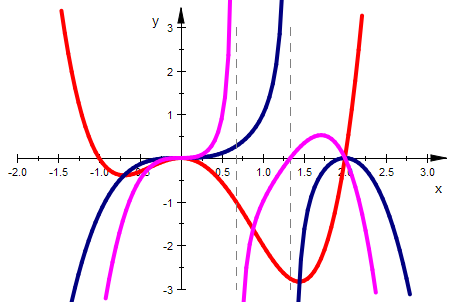
Nun also alles im animierten Graphen:
kuexg:=plot::Function2d(kurveextrema,x=-2..3, LineWidth=1,Color=RGB::DarkBlue):
kuwendg:=plot::Function2d(kurvewend,x=-2..3, LineWidth=1,Color=RGB::Magenta):
plot(fani,kuexg,kuwendg)
 !
!
Integrale
int(f(x,k), x)
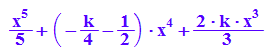
i2:=int(f(x,k), x=0..2)
![]()
i2 $ k=-1..3
![]()
Hierzu ist mir nichts Bemerkenswertes eingefallen.
-------------------------------------------------------------------------------------------------------
Für welches k wird das Intergral im Intervall [0,2] Null?
solve(i2=0,k)

in1:=plot::Integral(fanika,10)
![]()
plot(in1,fani,fanika)
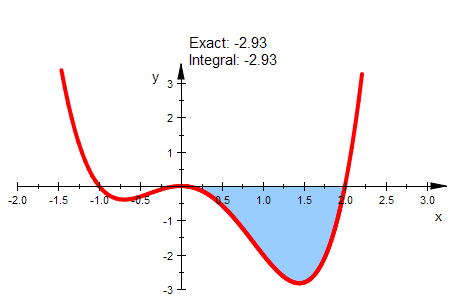

f(x,6/5)
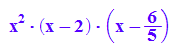
plotfunc2d(f(x,6/5), x=-1..3,YRange=-1..1,
Scaling=Constrained)
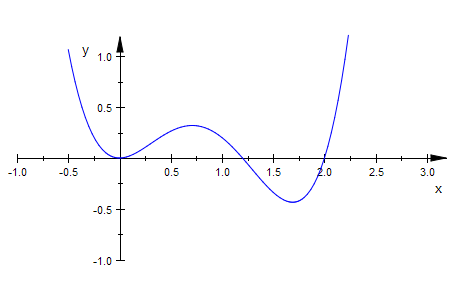
Bei der Scharkurve mit x=6/5 halten sich also die Flächen über und unter der x-Achse
gerade die Waage.
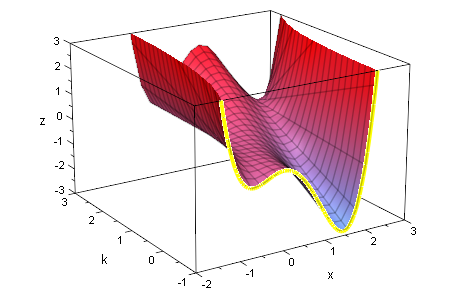
Es folgen einige 3-d-Graphen, die in der Vorlesung entstanden sind.
f(x,k)
![]()
plotfunc3d(f(x,k))
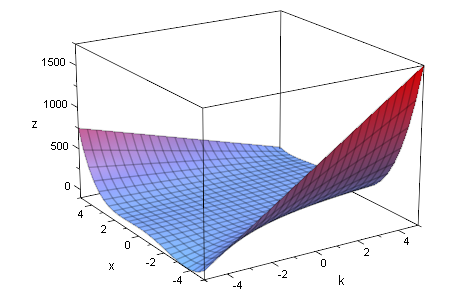
fxkg:=plot::Function3d(f(x,k),x=-2..3,k=-1..3)
![]()
plot(fxkg)
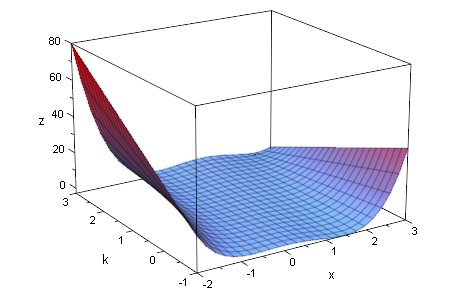
fxkg2:=plot::Function3d(f(x,k),x=-2..3,k=-1..3,ViewingBoxZRange=-3..3):
plot(fxkg2)
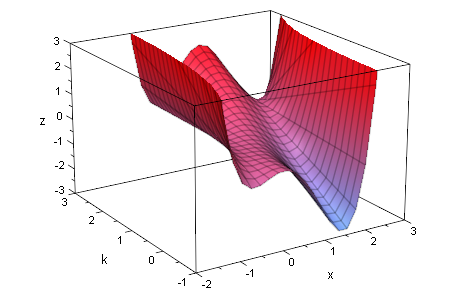
g:=(x,y)->x^2*y
![]()
form:=plot::Function3d(g(x,y),x=-3..3,y=-1..2): plot(form)
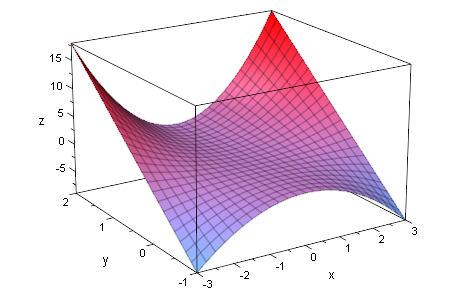
Hier wierd nun gezeigt, wie man die Grids wandern lässt.
geradeng:=plot::Curve3d([x,y,g(x,y)], x=-2..3,y=-1..3):
parg:=plot::Curve3d([x,y,g(x,y)], y=-1..3,x=-2..3):
plot(geradeng,parg,form)
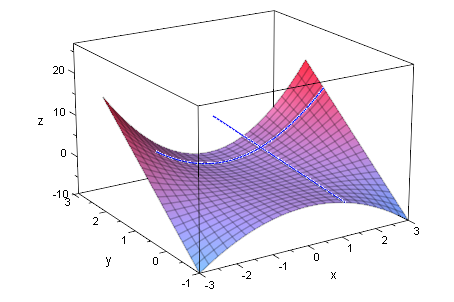

gerg:=plot::Curve3d([x,k,f(x,k)], k=-1..3,x=-1..3,
LineWidth=1, LineColor=RGB::Green):
plot(gerg,fxkg2)
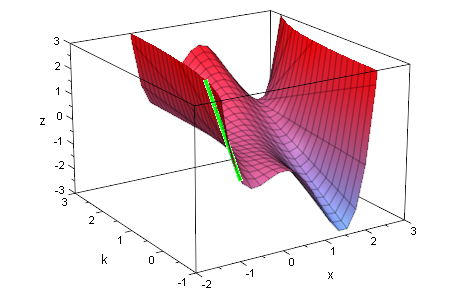

polyg:=plot::Curve3d([x,k,f(x,k)], x=-2..3,k=-1..3,
LineWidth=1,LineColor=[1,1,0]):
plot(polyg,fxkg2)