Download des MuPAD-Notebooks (240 KB) Save Link Taget As..., Verküpfung speichern unter...
 Kurvenschar-Diskussion
Kurvenschar-Diskussion
Analysis mit MuPAD, mit Kurven der Extrema und der Wendepunkte
Prof. Dr.Dörte Haftendorn, Juni 04
-----------------------------------------------------------------------------------
- f:=(x,k)->x^2*(x-k)*(x-2)
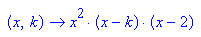
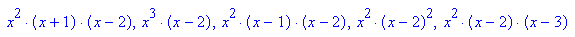
- plotfunc2d(alle,x=-1.2..3,y=-3..3,
Scaling=Constrained,GridLines=Automatic)
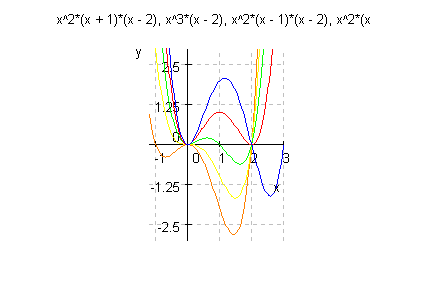

Die Nullstellen sind hier offensichtlich: Gemeinsame doppelte Nullstelle x=0, Berührung,
Gemeinsame Nullestelle bei x=2, weitere Nullstalle bei x=k.
Für k=2 ist auch diese Nullstelle doppelt, also Berührung, sonst ist sie einfach.
für k=0 ist die bei x=0 dreifach, also Sattel, sonst sind alle anderen Nullstellen einfach.
Automatische Bestimmung der Nullstellen:
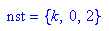
Die Vielfachheiten sind nicht zu sehen. Die Klammerform ist aussagekräftiger.
- solve(f(x,k)=0,x, Multiple)
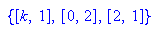
Multiple gibt die Vielfachheit mit aus.
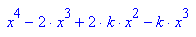
Wenn nun diese Form gegeben wäre, könnte man die Klammerform herstellen.
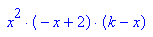
Ableitung und zugehörige Rechnungen
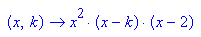
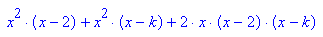
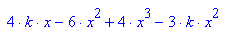
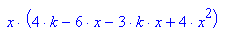
- plotfunc2d(subs(ableit, k=2),x=-3..3,y=-3..3)
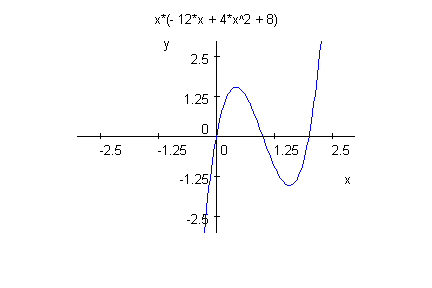

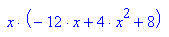
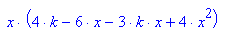
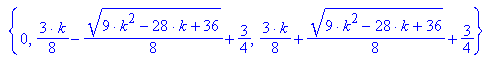
- extremstellen:=float(xe) $ k=-1..2
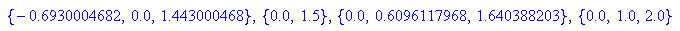
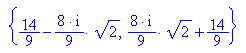
Die Diskriminate wird nie Null, damit existieren i.a. drei Extrempounkte.
Für k=2
- extremwertek:=f(op(xe,i),k) $i=1..nops(xe):
- map(extremwertek,expand):// Wahnsinnsterme!!!
- [k,map(extremwertek,float)] $ k=-1..2
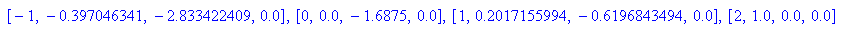
Kurve der Extrema
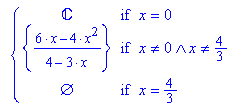
Die Gleichung Ableitung=0 ist nach k aufzulösen.
Von diesen ist die mittlere die gesuchte.
Dieser Term ist für k in f(x,k) einzusetzen
- kurveextrema:=subs(f(x,k),k=(6*x-4*x^2)/(4-3*x))
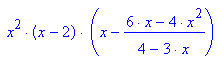
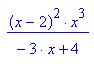
Dieses ist der Funktionsterm der Kurve der Extrema.
Man sieht einen Sattel bei 0, einen Pol bei x=4/3 und eine doppelte Nullstelle bei 2.
- plotfunc2d(alle,kurveextrema,x=-1.2..3,y=-3..3,
Scaling=Constrained,GridLines=Automatic)
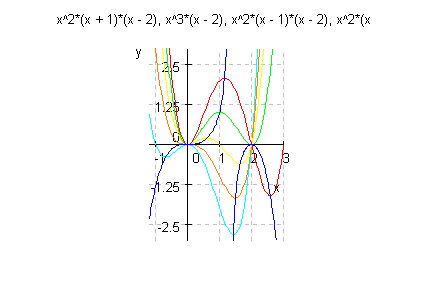

Hier sieht man, dass die Kurve der Extrem (hier blau) gut passt.
Wendepunkte
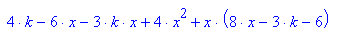
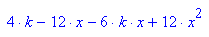
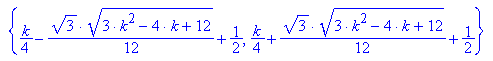
Das unangenehme Terme.
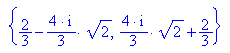
Die Diskriminante wird aber nie Null, damit exitieren
stets zwei Wendepunkte.
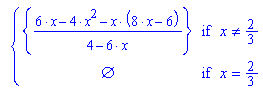
- kurvewend:=subs(f(x,k),k=(-12*x^2+12*x)/(4-6*x))
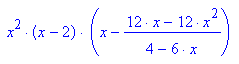
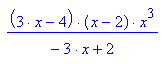
Auch die Kurve der Wendepunkte hat einen Sattel im Ursprung.
Sie hat einen Pol bei x=2/3 und einfache Nullstellen bei x=4/3 und x=2.
- plotfunc2d(alle,kurveextrema,kurvewend,x=-1.2..3,y=-3..3,
Scaling=Constrained,GridLines=Automatic)
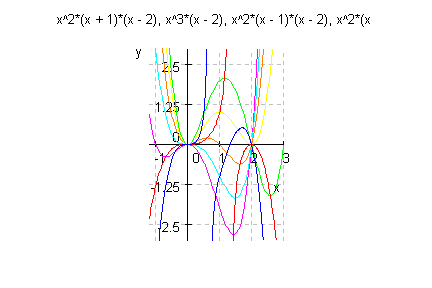

Auch die Kurve der Wendpunkte (hier blau) passt gut.
Integrale
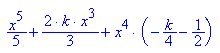
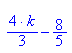
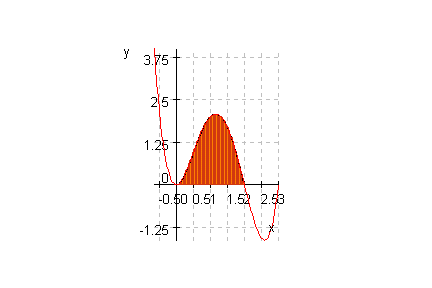
- f3 := plot::Function2d(f(x,3), x = -1..3,y=-3..4):
- p := student::plotRiemann(f(x,3), x = 0..2, 50):
plot(p,f3,Scaling=Constrained,GridLines=Automatic)

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]
[haftendorn.uni-lueneburg.de/ing-math]


 [LBS-Mathe] [Analysis]
[LBS-Mathe] [Analysis]
Inhalt und Webbetreuung Prof. Dr. Dörte Haftendorn  April. 2003, update 15. August 2011
April. 2003, update 15. August 2011
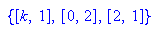
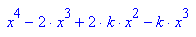
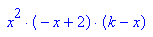
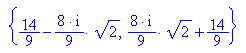
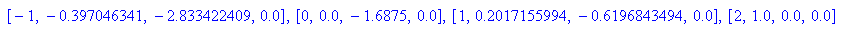
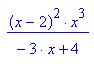


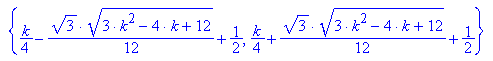
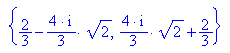
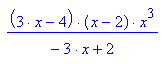


![]()
![]()
![]()
![]() [LBS-Mathe] [Analysis]
[LBS-Mathe] [Analysis] ![]() April. 2003, update
April. 2003, update