Kosinuswundern x^k Cos (1/x)
Prof. Dr. Dörte Haftendorn Ha /02

In[737]:=

f[x_] := Cos[1/x] ; f[0] = 0 ; f '[x] f[h]/h (* Differenzenquotient für x = 0 *) f ''[x] ... 1}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;

Out[738]=

sin(1/x)/x^2

Out[739]=

cos(1/h)/h

Out[740]=

-cos(1/x)/x^4 - (2 sin(1/x))/x^3

[Graphics:coswunder_6.gif]

In[742]:=

Limit[f[x], x -> 0] (* nicht stetig in x = 0 *) Limit[f '[x], x -> 0] Limit[f[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . nicht *)

Out[742]=

Interval[{-1, 1}]

Out[743]=

Interval[{-∞, ∞}]

Out[744]=

Interval[{-∞, ∞}]

In[745]:=

h[x_] := x Cos[1/x] h '[x] h[k]/k (* Differenzenquotient für x = 0 *) h ''[x] hGraph = Pl ... x}, {x, -2, 2}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;

Out[746]=

cos(1/x) + sin(1/x)/x

Out[747]=

cos(1/k)

Out[748]=

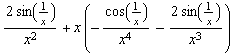
(2 sin(1/x))/x^2 + x (-cos(1/x)/x^4 - (2 sin(1/x))/x^3)

[Graphics:coswunder_15.gif]

In[750]:=

Limit[h[x], x -> 0] Limit[h '[x], x -> 0] Limit[h[k]/k, k -> 0] (* Differenzialquotient für x = 0 ex . nicht *) Limit[h ' '[x], x -> 0]

Out[750]=

0

Out[751]=

Interval[{-∞, ∞}]

Out[752]=

Interval[{-1, 1}]

Out[753]=

Interval[{-∞, ∞}]

•Asyptotengewinnung aus der Taylorreihe

•Tranformation xCos[1/x] - asy(x) Overscript[->, x -> ∞] 0 in 1/z Cos[z] - asy[1/z] Overscript[->, z -> 0] 0

In[754]:=

tay[z_] := Normal[Series[Cos[z], {z, 0, 6}]]

In[755]:=

Clear[asy] ; (1/z tay[z] // Expand) - asy

Out[755]=

-z^5/720 + z^3/24 - z/2 - asy + 1/z

•Wenn dieser Term für z->0 gegen 0 gehen soll, muss  gleten:

In[756]:=

asy = (1/z) /. z -> 1/x

Out[756]=

x

In[757]:=

hhAsyGraph = Plot[{h[x], x, x}, {x, -3, 2}, PlotStyle -> farbig, PlotRange -> {-1, 2}, AspectRatio -> Automatic] ;

[Graphics:coswunder_29.gif]

In[758]:=

Limit[h[x] - x, x -> ∞] (* Asymptote y = x *) Limit[h '[x] - 1, x -> ∞] Limit[h ''[x], x -> ∞]

Out[758]=

0

Out[759]=

0

Out[760]=

0

In[761]:=

hh[x_] := x^2 Cos[1/x] hh '[x] hh[h]/h (* Differenzenquotient für x = 0 *) hh ''[x]

Out[762]=

2 x cos(1/x) + sin(1/x)

Out[763]=

h cos(1/h)

Out[764]=

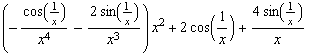
(-cos(1/x)/x^4 - (2 sin(1/x))/x^3) x^2 + 2 cos(1/x) + (4 sin(1/x))/x

In[765]:=

hhGraph = Plot[{hh[x], x^2, -x^2}, {x, -2, 2}, PlotStyle -> farbig, PlotRange -> {-1, 1}, AspectRatio -> Automatic] ;

[Graphics:coswunder_39.gif]

In[766]:=

Limit[hh[x], x -> 0] Limit[hh '[x], x -> 0] (* nicht stetig in x = 0 *) Limit[hh[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . *) Limit[hh ' '[x], x -> 0]

Out[766]=

0

Out[767]=

Interval[{-1, 1}]

Out[768]=

0

Out[769]=

Interval[{-∞, ∞}]

•Asyptotengewinnung aus der Taylorreihe

•Tranformation x^2 Cos[1/x] - asy(x) Overscript[->, x -> ∞] 0 in 1/z^2 Cos[z] - asy[1/z] Overscript[->, z -> 0] 0

In[770]:=

tay[z_] := Normal[Series[Cos[z], {z, 0, 6}]]

In[771]:=

Clear[asyy] ; (1/z^2 tay[z] // Expand) - asyy

Out[771]=

-z^4/720 + z^2/24 - asyy - 1/2 + 1/z^2

•Wenn dieser Term für z->0 gegen 0 gehen soll, muss  gleten:

In[772]:=

asyy = (1/z^2 - 1/2) /. z -> 1/x

Out[772]=

x^2 - 1/2

In[773]:=

hhAsyGraph = Plot[{hh[x], x^2, x^2 - 1/2}, {x, -3, 2}, PlotStyle -> farbig, PlotRange -> {-1, 2}, AspectRatio -> Automatic] ;

[Graphics:coswunder_53.gif]

In[774]:=

Limit[hh[x] - x^2 + 1/2, x -> ∞] (* Asymptote y = x^2 - 1/2 *) Limit[hhh '[x] - 2 x, x -> ∞] Limit[hhh ''[x] - 2, x -> ∞]

Out[774]=

0

Out[775]=

0

Out[776]=

0

In[777]:=

hhh[x_] := x^3 Cos[1/x] hhh '[x] hhh[h]/h (* Differenzenquotient für x = 0 *) hhh ''[x]

Out[778]=

3 cos(1/x) x^2 + sin(1/x) x

Out[779]=

h^2 cos(1/h)

Out[780]=

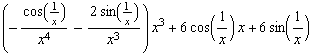
(-cos(1/x)/x^4 - (2 sin(1/x))/x^3) x^3 + 6 cos(1/x) x + 6 sin(1/x)

In[781]:=

hhhGraph = Plot[{hhh[x], x^3, -x^3}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;

[Graphics:coswunder_63.gif]

In[782]:=

Limit[hhh[x], x -> 0] Limit[hhh '[x], x -> 0] (* stetig in x = 0 *) Limit[hhh[h]/h, h -& ... ferenzialquotient für x = 0 *) Limit[hhh ' '[x], x -> 0] (* Unbeschränkt in x = 0 *)

Out[782]=

0

Out[783]=

0

Out[784]=

0

Out[785]=

Interval[{-∞, ∞}]

•Asyptotengewinnung aus der Taylorreihe

•Tranformation x^3 Cos[1/x] - asy(x) Overscript[->, x -> ∞] 0 in 1/z^3 Cos[z] - asy[1/z] Overscript[->, z -> 0] 0

In[786]:=

tay[z_] := Normal[Series[Cos[z], {z, 0, 6}]]

In[787]:=

Clear[asyyy] ; (1/z^3 tay[z] // Expand) - asyyy

Out[787]=

-z^3/720 + z/24 - asyyy - 1/(2 z) + 1/z^3

•Wenn dieser Term für z->0 gegen 0 gehen soll, muss  gleten:

In[788]:=

asyyy = (1/z^3 - 1/(2 z)) /. z -> 1/x

Out[788]=

x^3 - x/2

In[789]:=

hhhAsyGraph = Plot[{hhh[x], x^3, -x^3, x^3 - 1/2 x}, {x, -1, 2}, PlotStyle -> farbig, PlotRange -> {-1/2, 2}, AspectRatio -> Automatic] ;

[Graphics:coswunder_77.gif]

In[790]:=

Limit[hhh[x] - x^3 + 1/2 x, x -> ∞] (* Asymptote y = x^3 - 1/2 x *) Limit[hhh '[x] - 3 x^2 + 1/2, x -> ∞] Limit[hhh ''[x] - 6 x, x -> ∞]

Out[790]=

0

Out[791]=

0

Out[792]=

0

In[793]:=

hhhh[x_] := x^4 Cos[1/x] hhhh '[x] hhhh[h]/h (* Differenzenquotient für x = 0 *) hhhh ''[x]

Out[794]=

4 cos(1/x) x^3 + sin(1/x) x^2

Out[795]=

h^3 cos(1/h)

Out[796]=

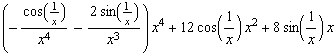
(-cos(1/x)/x^4 - (2 sin(1/x))/x^3) x^4 + 12 cos(1/x) x^2 + 8 sin(1/x) x

In[797]:=

hhhhGraph = Plot[{hhhh[x], x^4, -x^4}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;

[Graphics:coswunder_87.gif]

In[798]:=

Limit[hhhh[x], x -> 0] Limit[hhhh '[x], x -> 0] Limit[hhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhh ' '[x], x -> 0]

Out[798]=

0

Out[799]=

0

Out[800]=

0

Out[801]=

Underscript[lim, x -> 0] (12 cos(1/x) x^2 + 6 sin(1/x) x - cos(1/x))

•Asyptotengewinnung aus der Taylorreihe

•Tranformation x^4 Cos[1/x] - asy(x) Overscript[->, x -> ∞] 0 in 1/z^4 Cos[z] - asy[1/z] Overscript[->, z -> 0] 0

In[802]:=

tay[z_] := Normal[Series[Cos[z], {z, 0, 6}]]

In[825]:=

Clear[asyyyy] ; (1/z^4 tay[z] // Expand) - asyyyy

Out[825]=

-z^2/720 - asyyyy + 1/24 - 1/(2 z^2) + 1/z^4

•Wenn dieser Term für z->0 gegen 0 gehen soll, muss  gleten:

In[826]:=

asyyyy = (1/z^4 - 1/(2 z^2) + 1/24) /. z -> 1/x

Out[826]=

x^4 - x^2/2 + 1/24

In[805]:=

hhhAsyGraph = Plot[{hhhh[x], x^3, -x^3, asyyyy}, {x, -0.7, 0.7}, PlotStyle -> farbig, PlotRange -> {-0.05, 0.1}] ;

[Graphics:coswunder_101.gif]

In[806]:=

Limit[hhhh[x] - asyyyy, x -> ∞] (* Asymptote y = x^4 - 1/2 x^2 + 1/24 *) Limit[hhhh '[x] - 4 x^3 + x, x -> ∞] Limit[hhhh ''[x] - 12 x^2 + 1, x -> ∞]

Out[806]=

0

Out[807]=

0

Out[808]=

0

In[809]:=

hhhhh[x_] := x^5 Cos[1/x] hhhhh '[x] hhhhh[h]/h (* Differenzenquotient für x = 0 *) hhhhh ''[x] <br />

Out[810]=

5 cos(1/x) x^4 + sin(1/x) x^3

Out[811]=

h^4 cos(1/h)

Out[812]=

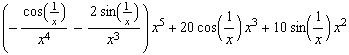
(-cos(1/x)/x^4 - (2 sin(1/x))/x^3) x^5 + 20 cos(1/x) x^3 + 10 sin(1/x) x^2

In[813]:=

hhhhhGraph = Plot[{hhhhh[x], x^5, -x^5}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;

[Graphics:coswunder_111.gif]

In[814]:=

Limit[hhhhh[x], x -> 0] Limit[hhhhh '[x], x -> 0] Limit[hhhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhhh ' '[x], x -> 0]

Out[814]=

0

Out[815]=

0

Out[816]=

0

Out[817]=

0

•Asyptotengewinnung aus der Taylorreihe

•Tranformation x^5 Cos[1/x] - asy(x) Overscript[->, x -> ∞] 0 in 1/z^5 Cos[z] - asy[1/z] Overscript[->, z -> 0] 0

In[818]:=

tay[z_] := Normal[Series[Cos[z], {z, 0, 6}]]

In[827]:=

Clear[asyyyyy] ; (1/z^5 tay[z] // Expand) - asyyyyy

Out[827]=

-asyyyyy - z/720 + 1/(24 z) - 1/(2 z^3) + 1/z^5

•Wenn dieser Term für z->0 gegen 0 gehen soll, muss  gleten:

In[828]:=

asyyyyy = (1/z^5 - 1/(2 z^3) + 1/(24 z)) /. z -> 1/x

Out[828]=

x^5 - x^3/2 + x/24

In[821]:=

hhhAsyGraph = Plot[{hhhhh[x], x^3, -x^3, asyyyyy}, {x, -0.7, 0.7}, PlotStyle -> farbig, PlotRange -> {-0.05, 0.1}] ;

[Graphics:coswunder_125.gif]

In[822]:=

Limit[hhhhh[x] - asyyyyy, x -> ∞] (* Asymptote y = x^5 - 1/2 x^3 + 1/24 x *) Limit[hh ... [x] - 5 x^4 + 3/2 x^2 - 1/24, x -> ∞] Limit[hhhhh ''[x] - 20 x^3 + 3 x, x -> ∞]

Out[822]=

0

Out[823]=

0

Out[824]=

0

Converted by Mathematica  (July 27, 2003)