www.mathematik-verstehen.de
Sinuswundern 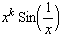
Prof. Dr. Dörte Haftendorn Ha 6/99 6/01 7/03
![f[x_] := Sin[1/x] ; f[0] = 0 ; f '[x] f[h]/h (* Differenzenquotient für x = 0 *) f ''[x] ... 1}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;](index_2.gif)
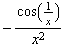
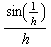
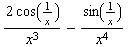
![[Graphics:index_6.gif]](index_6.gif)
![Limit[f[x], x -> 0] (* nicht stetig in x = 0 *) <br /> Limit[f '[x], x -> 0] <br /> Limit[f[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . nicht *)](index_7.gif)
![Interval[{-1, 1}]](index_8.gif)
![Interval[{-∞, ∞}]](index_9.gif)
![Interval[{-∞, ∞}]](index_10.gif)
![h[x_] := x Sin[1/x] h '[x] h[k]/k (* Differenzenquotient für x = 0 *) h ''[x] hGraph = Pl ... x}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;](index_11.gif)
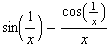
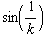
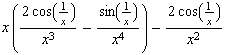
![[Graphics:index_15.gif]](index_15.gif)
![Limit[h[x], x -> 0] Limit[h '[x], x -> 0] Limit[h[k]/k, k -> 0] (* Differenzialquotient für x = 0 ex . nicht *) Limit[h ' '[x], x -> 0]](index_16.gif)
![Interval[{-∞, ∞}]](index_18.gif)
![Interval[{-1, 1}]](index_19.gif)
![Interval[{-∞, ∞}]](index_20.gif)
•Asyptotengewinnung aus der Taylorreihe
•Tranformation ![xSin[1/x] - asy(x) Overscript[->, x -> ∞] 0](index_21.gif) in
in ![1/z Sin[z] - asy[1/z] Overscript[->, z -> 0] 0](index_22.gif)
![tay[z_] := Normal[Series[Sin[z], {z, 0, 6}]]](index_23.gif)
![Clear[as] ; (1/z tay[z] // Expand) - as](index_24.gif)
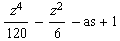
•Wenn dieser Term für z->0 gegen 0 gehen soll, muss gelten:
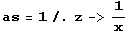
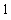
![hAsyGraph = Plot[{h[x], x, -x, 1}, {x, -3, 2}, PlotStyle -> farbig, PlotRange -> {-1, 2}, AspectRatio -> Automatic] ;](index_28.gif)
![[Graphics:index_29.gif]](index_29.gif)
![Limit[h[x] - 1, x -> ∞] (* Asymptote y = 1 *) Limit[h '[x], x -> ∞] Limit[h ''[x], x -> ∞]](index_30.gif)
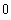
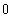
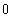
![hh[x_] := x^2 Sin[1/x] hh '[x] hh[h]/h (* Differenzenquotient für x = 0 *) hh ''[x]](index_34.gif)
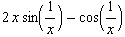
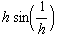
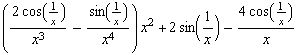
![hhGraph = Plot[{hh[x], x^2, -x^2}, {x, -2, 2}, PlotStyle -> farbig, PlotRange -> {-1, 1}, AspectRatio -> Automatic] ;](index_38.gif)
![[Graphics:index_39.gif]](index_39.gif)
![Limit[hh[x], x -> 0] Limit[hh '[x], x -> 0] <br /> (* nicht stetig in x = 0 *) Limit[hh[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . *) Limit[hh ' '[x], x -> 0]](index_40.gif)
![Interval[{-1, 1}]](index_42.gif)
![Interval[{-∞, ∞}]](index_44.gif)
•Asyptotengewinnung aus der Taylorreihe
•Tranformation ![x^2 Sin[1/x] - asy(x) Overscript[->, x -> ∞] 0](index_45.gif) in
in ![1/z^2 Sin[z] - asy[1/z] Overscript[->, z -> 0] 0](index_46.gif)
![tay[z_] := Normal[Series[Sin[z], {z, 0, 7}]]](index_47.gif)
![Clear[ass] ; (1/z^2 tay[z] // Expand) - ass](index_48.gif)
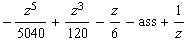
•Wenn dieser Term für z->0 gegen 0 gehen soll, muss gelten:
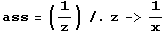
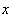
![hhAsyGraph = Plot[{hh[x], x^2, -x^2, x}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-3, 3}, AspectRatio -> Automatic] ;](index_52.gif)
![[Graphics:index_53.gif]](index_53.gif)
![Limit[hh[x] - x, x -> ∞] (* Asymptote y = x *) Limit[hh '[x] - 1, x -> ∞] Limit[hh ''[x], x -> ∞]](index_54.gif)
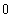
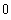
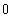
![hhh[x_] := x^3 Sin[1/x] hhh '[x] hhh[h]/h (* Differenzenquotient für x = 0 *) hhh ''[x]](index_58.gif)
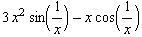
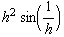
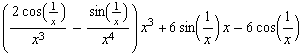
![hhhGraph = Plot[{hhh[x], x^3, -x^3}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;](index_62.gif)
![[Graphics:index_63.gif]](index_63.gif)
![Limit[hhh[x], x -> 0] <br /> Limit[hhh '[x], x -> 0] (* stetig in x = 0 *) <br /> Limit[ ... ferenzialquotient für x = 0 *) Limit[hhh ' '[x], x -> 0] (* Unbeschränkt in x = 0 *)](index_64.gif)
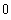
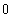
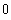
![Interval[{-∞, ∞}]](index_68.gif)
•Asyptotengewinnung aus der Taylorreihe
•Tranformation ![x^3 Sin[1/x] - asy(x) Overscript[->, x -> ∞] 0](index_69.gif) in
in ![1/z^3 Sin[z] - asy[1/z] Overscript[->, z -> 0] 0](index_70.gif)
![tay[z_] := Normal[Series[Sin[z], {z, 0, 7}]]](index_71.gif)
![Clear[asss] ; (1/z^3 tay[z] // Expand) - asss](index_72.gif)
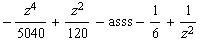
•Wenn dieser Term für z->0 gegen 0 gehen soll, muss gelten:
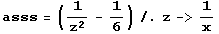
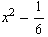
![hhhAsyGraph = Plot[{hhh[x], x^3, -x^3, x^2 - 1/6}, {x, -1, 1}, PlotStyle -> farbig, PlotRange -> {-0.1, 1}, AspectRatio -> Automatic] ;](index_76.gif)
![[Graphics:index_77.gif]](index_77.gif)
![Limit[hhh[x] - x^2 + 1/6, x -> ∞] (* Asymptote y = x^2 - 1/6 *) Limit[hhh '[x] - 2 x, x -> ∞] Limit[hhh ''[x] - 2, x -> ∞]](index_78.gif)
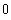
![hhhh[x_] := x^4 Sin[1/x] hhhh '[x] hhhh[h]/h (* Differenzenquotient für x = 0 *) hhhh ''[x]](index_82.gif)
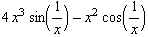
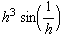
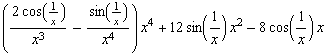
![hhhhGraph = Plot[{hhhh[x], x^4, -x^4}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;](index_86.gif)
![[Graphics:index_87.gif]](index_87.gif)
![Limit[hhhh[x], x -> 0] Limit[hhhh '[x], x -> 0] Limit[hhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhh ' '[x], x -> 0]](index_88.gif)

•Asyptotengewinnung aus der Taylorreihe
•Tranformation ![x^4 Sin[1/x] - asy(x) Overscript[->, x -> ∞] 0](index_93.gif) in
in ![1/z^4 Sin[z] - asy[1/z] Overscript[->, z -> 0] 0](index_94.gif)
![tay[z_] := Normal[Series[Sin[z], {z, 0, 7}]]](index_95.gif)
![Clear[assss] ; (1/z^4 tay[z] // Expand) - assss](index_96.gif)
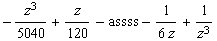
•Wenn dieser Term für z->0 gegen 0 gehen soll, muss gelten:
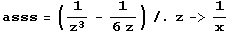
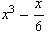
![hhhhAsyGraph = Plot[{hhhh[x], x^4, -x^4, x^3 - 1/6 x}, {x, -0.7, 0.7}, PlotStyle -> farbig, PlotRange -> {-0.3, .3}] ;](index_100.gif)
![[Graphics:index_101.gif]](index_101.gif)
![Limit[hhhh[x] - x^3 + 1/6 x, x -> ∞] (* Asymptote y = x^3 - 1/6 x *) Limit[hhhh '[x] - 3 x^2 + 1/6, x -> ∞] Limit[hhhh ''[x] - 6 x, x -> ∞]](index_102.gif)
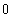
![hhhhh[x_] := x^5 Sin[1/x] hhhhh '[x] hhhhh[h]/h (* Differenzenquotient für x = 0 *) hhhhh ''[x]](index_106.gif)
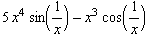
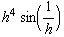
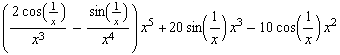
![hhhhhGraph = Plot[{hhhhh[x], x^5, -x^5}, {x, -.1, .1}, PlotStyle -> farbig (* , PlotRange -> {-0.1, 1}, AspectRatio -> Automatic *)] ;](index_110.gif)
![[Graphics:index_111.gif]](index_111.gif)
![Limit[hhhhh[x], x -> 0] Limit[hhhhh '[x], x -> 0] Limit[hhhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhhh ' '[x], x -> 0]](index_112.gif)
•Asyptotengewinnung aus der Taylorreihe
•Tranformation ![x^5 Sin[1/x] - asy(x) Overscript[->, x -> ∞] 0](index_117.gif) in
in ![1/z^5 Sin[z] - asy[1/z] Overscript[->, z -> 0] 0](index_118.gif)
![tay[z_] := Normal[Series[Sin[z], {z, 0, 7}]]](index_119.gif)
![Clear[asssss] ; (1/z^5 tay[z] // Expand) - asssss](index_120.gif)
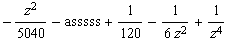
•Wenn dieser Term für z->0 gegen 0 gehen soll, muss gelten:
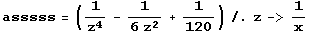
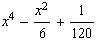
![hhhhhAsyGraph = Plot[{hhhhh[x], x^5, -x^5, x^4 - 1/6 x^2 + 1/120}, {x, -0.5, 0.5}, PlotStyle -> farbig, PlotRange -> {-0.001, .02}] ;](index_124.gif)
![[Graphics:index_125.gif]](index_125.gif)
![Limit[hhhhh[x] - x^4 + 1/6 x^2 - 1/120, x -> ∞] (* Asymptote y = x^4 - 1/6 x^2 + 1/12 ... t[hhhhh '[x] - 4 x^3 + 1/3 x, x -> ∞] Limit[hhhhh ''[x] - 12 x^2 + 1/3, x -> ∞]](index_126.gif)
Converted by Mathematica
(July 27, 2003)
![f[x_] := Sin[1/x] ; f[0] = 0 ; f '[x] f[h]/h (* Differenzenquotient für x = 0 *) f ''[x] ... 1}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;](index_2.gif)
![]()
![]()
![]()
![[Graphics:index_6.gif]](index_6.gif)
![Limit[f[x], x -> 0] (* nicht stetig in x = 0 *) <br /> Limit[f '[x], x -> 0] <br /> Limit[f[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . nicht *)](index_7.gif)
![]()
![]()
![]()
![h[x_] := x Sin[1/x] h '[x] h[k]/k (* Differenzenquotient für x = 0 *) h ''[x] hGraph = Pl ... x}, {x, -3, 3}, PlotStyle -> farbig, PlotRange -> {-1, 1.5}, AspectRatio -> Automatic] ;](index_11.gif)
![]()
![]()
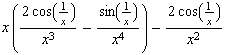
![[Graphics:index_15.gif]](index_15.gif)
![Limit[h[x], x -> 0] Limit[h '[x], x -> 0] Limit[h[k]/k, k -> 0] (* Differenzialquotient für x = 0 ex . nicht *) Limit[h ' '[x], x -> 0]](index_16.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:index_29.gif]](index_29.gif)
![Limit[h[x] - 1, x -> ∞] (* Asymptote y = 1 *) Limit[h '[x], x -> ∞] Limit[h ''[x], x -> ∞]](index_30.gif)
![]()
![]()
![]()
![hh[x_] := x^2 Sin[1/x] hh '[x] hh[h]/h (* Differenzenquotient für x = 0 *) hh ''[x]](index_34.gif)
![]()
![]()
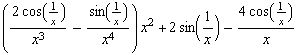
![]()
![[Graphics:index_39.gif]](index_39.gif)
![Limit[hh[x], x -> 0] Limit[hh '[x], x -> 0] <br /> (* nicht stetig in x = 0 *) Limit[hh[h]/h, h -> 0] (* Differenzialquotient für x = 0 ex . *) Limit[hh ' '[x], x -> 0]](index_40.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:index_53.gif]](index_53.gif)
![Limit[hh[x] - x, x -> ∞] (* Asymptote y = x *) Limit[hh '[x] - 1, x -> ∞] Limit[hh ''[x], x -> ∞]](index_54.gif)
![]()
![]()
![]()
![hhh[x_] := x^3 Sin[1/x] hhh '[x] hhh[h]/h (* Differenzenquotient für x = 0 *) hhh ''[x]](index_58.gif)
![]()
![]()
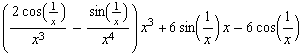
![]()
![[Graphics:index_63.gif]](index_63.gif)
![Limit[hhh[x], x -> 0] <br /> Limit[hhh '[x], x -> 0] (* stetig in x = 0 *) <br /> Limit[ ... ferenzialquotient für x = 0 *) Limit[hhh ' '[x], x -> 0] (* Unbeschränkt in x = 0 *)](index_64.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![hhhAsyGraph = Plot[{hhh[x], x^3, -x^3, x^2 - 1/6}, {x, -1, 1}, PlotStyle -> farbig, PlotRange -> {-0.1, 1}, AspectRatio -> Automatic] ;](index_76.gif)
![[Graphics:index_77.gif]](index_77.gif)
![Limit[hhh[x] - x^2 + 1/6, x -> ∞] (* Asymptote y = x^2 - 1/6 *) Limit[hhh '[x] - 2 x, x -> ∞] Limit[hhh ''[x] - 2, x -> ∞]](index_78.gif)
![]()
![]()
![]()
![hhhh[x_] := x^4 Sin[1/x] hhhh '[x] hhhh[h]/h (* Differenzenquotient für x = 0 *) hhhh ''[x]](index_82.gif)
![]()
![]()
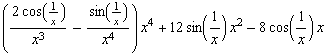
![]()
![[Graphics:index_87.gif]](index_87.gif)
![Limit[hhhh[x], x -> 0] Limit[hhhh '[x], x -> 0] Limit[hhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhh ' '[x], x -> 0]](index_88.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:index_101.gif]](index_101.gif)
![Limit[hhhh[x] - x^3 + 1/6 x, x -> ∞] (* Asymptote y = x^3 - 1/6 x *) Limit[hhhh '[x] - 3 x^2 + 1/6, x -> ∞] Limit[hhhh ''[x] - 6 x, x -> ∞]](index_102.gif)
![]()
![]()
![]()
![hhhhh[x_] := x^5 Sin[1/x] hhhhh '[x] hhhhh[h]/h (* Differenzenquotient für x = 0 *) hhhhh ''[x]](index_106.gif)
![]()
![]()
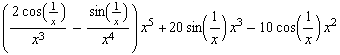
![]()
![[Graphics:index_111.gif]](index_111.gif)
![Limit[hhhhh[x], x -> 0] Limit[hhhhh '[x], x -> 0] Limit[hhhhh[h]/h, h -> 0] (* Differenzialquotient für x = 0 *) Limit[hhhhh ' '[x], x -> 0]](index_112.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![hhhhhAsyGraph = Plot[{hhhhh[x], x^5, -x^5, x^4 - 1/6 x^2 + 1/120}, {x, -0.5, 0.5}, PlotStyle -> farbig, PlotRange -> {-0.001, .02}] ;](index_124.gif)
![[Graphics:index_125.gif]](index_125.gif)
![Limit[hhhhh[x] - x^4 + 1/6 x^2 - 1/120, x -> ∞] (* Asymptote y = x^4 - 1/6 x^2 + 1/12 ... t[hhhhh '[x] - 4 x^3 + 1/3 x, x -> ∞] Limit[hhhhh ''[x] - 12 x^2 + 1/3, x -> ∞]](index_126.gif)
![]()
![]()
![]()