Extremwertaufgabe: Silberschmied Spitzpokal
Prof. Dr. Dörte Haftendorn, MuPAD 4, Sept.06 Update
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Mathix ist Silberschmied geworden. Er möchte Pokale schmieden, bei denen auf einen Kegel mit Raduis r und Höhe r ein offener Zylinder aufgesetzt ist. Er hat versucht auszurechnen, welche Zylinderhöhe und welchen Radius er bei festem Volumen (z.B.2 Liter) nehmen muss, damit er minimalen Silberverbrauch hat. Mathilde sagt: "Am besten lässt du den Zylinder weg, das war bei dem Pokal mit der Halbkugel auch am besten." Hat Mathilde Recht? (Variante mit halbkugelförmigem Unterteil siehe Extradatei)


Zielgröße: Silberverbrauch, entspricht der Oberfläche, setzt sich zusammen aus dem Zylindermantel und dem Kegelmantel (hh=h, weil h später gebraucht wird, s=Mantellinie):
Sformel:=2*PI*r*hh+PI*r*s;
![]()
Nebenbedingung, Volumen 2 Liter= 2000 cm^3, setzt sich zusammen aus Kegelvolumen und Zylindervolumen
delete V:
s:=sqrt(2)*r;
NB:= V=PI*r^2*hh+1/3*PI*r^3;
![]()
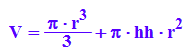
Nach r ließe sich diese Gleichung gar nicht leicht auflösen, daher Auflösen nach hh
assume(r>0): solve(NB,hh);
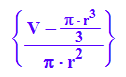
expand(op(%))
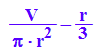
h:=r->V/(PI*r^2)-1/3*r;h(r);
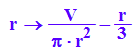
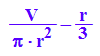
Aufstellen der Zielfunktion S in Abhängigkeit von r allein
S:=r->2*PI*r*h(r)+PI*r*s;S(r); expand(S(r)):
![]()
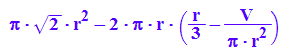
Man kann die Ausgabe markieren und in eine neue Ausgabezelle ziehen.
expand(2^(1/2)*PI*r^2 - 2*PI*r*(1/3*r - 1/PI*V/r^2));
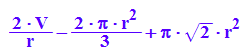
S:=r->2*V/r - 2/3*PI*r^2 + 2^(1/2)*PI*r^2: S(r); //Zielfunktion
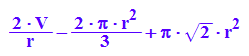
Aufbau der Zielfunktion aus Bausteinen:
Nun wird das Volumen auf 2 Liter=2000cm^3 festgesetzt.
V:=2000: //Längen in cm
plotfunc2d(2*V/r,S(r), - 2/3*PI*r^2 + 2^(1/2)*PI*r^2,r=0..16,
ViewingBoxYRange=0..1000 );
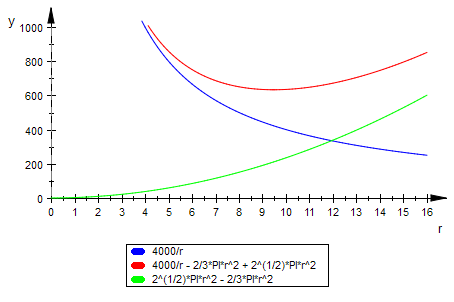
Als Summe aus Parabel und Hyperbel hat die Zielfunktion ein gesichertes Minimum, etwa bei r=10.
Berechnung:
S'(r);
solve(S'(r)=0,r);
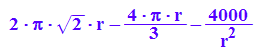

rs:=float(%[1])
![]()
Welches ist das maximale r, für welchel die 2 Liter ganz in dem Kegel sind?
Wenn r noch größer würde, wäre der Pokal ja zu groß.
Berechnung aus dem Kegelvolumen:
V:=2000:
solve(V=1/3*PI*r^3,r);
rm:=(op(%));rmf:=float(rm);
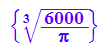
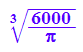
![]()
Da ergibt sich ein größerer Wert, darum hat der Pokal mit minimalem Verbrauch
einen zylindischen Rand mit folgender Höhe:
simplify(h(rs));
![]()
Damit ist klar, dass Mathilde nicht Recht hat, der Pokal für 2 Liter mit minimalem Silberverbrauch hat einen
Zylinderrand von fast 4 cm. Die Silberoberfläche ist dann
simplify(S(rs));
float(%)
![]()
![]()
####################################################################
Herstellung der Graphen:
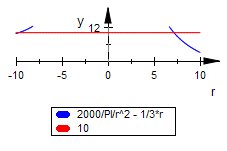
Sinnvolle optische Begrenzung für h könnte 10 sein. Wie groß ist dann r
solve(h(r)=10,r)
![]()
Exakt geht es nicht, also Ablesen:
plotfunc2d(h(r),10,r=-10..10,ViewingBoxYRange=0..12 )
Numerische Bestimmung:
lo:=numeric::solve(h(r)=10,r);
lm:=numeric::solve(h(r)=0,r)
![]()
![]()
rmin:=lo[3];
rmax:=lm[1];
![]()
![]()
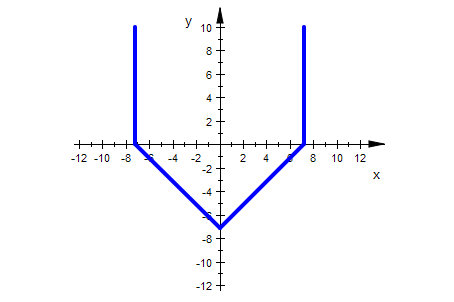
gerli2d:=plot::Line2d([-r,0],[0,-r],r=rmin..rmax):
gerre2d:=plot::Line2d([r,0],[0,-r],r=rmin..rmax):
zy2d1:=plot::Line2d([-r,0],[-r,h(r)],r=rmin..rmax ):
zy2d2:=plot::Line2d([r,0],[r,h(r)],r=rmin..rmax):
plot(gerli2d, gerre2d,zy2d1,zy2d2, ViewingBoxYRange=-rmax..10,
LineWidth=1, Scaling=Constrained):

hkeg3d:=plot::Surface([k*cos(t),k*sin(t),-r+k],
t=0..2*PI,k=0..r , r=rmin..rmax):
zyl3d:=plot::Surface([r*cos(t),r*sin(t),hh],t=0..2*PI,hh=0..h(r),
r=rmin..rmax, ViewingBoxZRange=-rmax..10,
AnimationStyle=BackAndForth):
plot(hkeg3d,zyl3d)
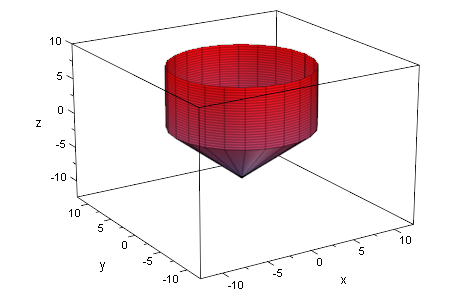

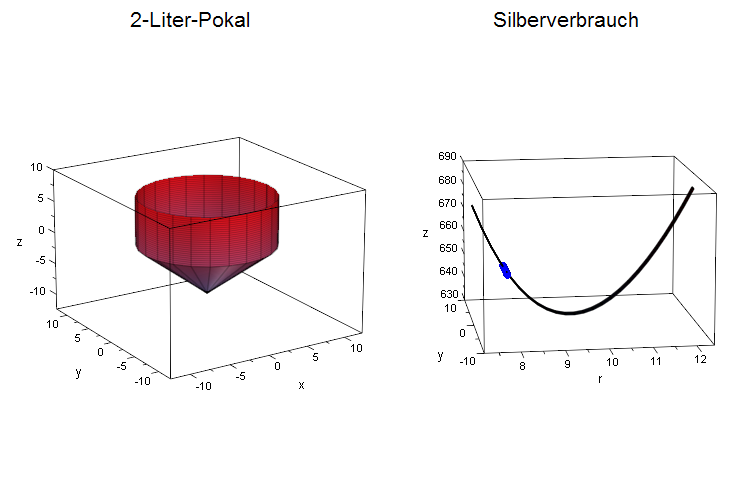
Gezeigt sind verschiedene Pokale mit 2 Liter Inhalt.
###############################################################
Darstellung der Zielfunktion allein und eines animierten Silververbrauchspunktes
Sg:=plot::Function2d(S(r),r=rmin..rmax, LineColor=[1,0,0]):
pkt:=plot::Point2d([r,S(r)],r=rmin..rmax, PointSize=5,
PointStyle=XCrosses):
Definition von Szenen, damit man alles zusammen sehen kann.
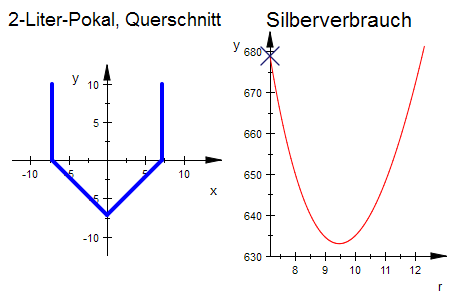
scen1:=plot::Scene2d(gerli2d,gerre2d,zy2d1,zy2d2,
ViewingBoxYRange=-rmax..10,LineWidth=1, Scaling=Constrained,
AnimationStyle=BackAndForth,
Header="2-Liter-Pokal, Querschnitt",HeaderFont = ["arial", 14]):
scen2:=plot::Scene2d(Sg,pkt, ViewingBoxYRange=630..680,
AnimationStyle=BackAndForth,
Header="Silberverbrauch", HeaderFont = ["arial", 16]):
plot(scen1, scen2):

Leider können 2d- und 3d-Szenen micht in denselben plot.
Darum Simulation von 2d in 3d.
SWand:=plot::Function3d(S(r),r=rmin..rmax,y=0..1,
ViewingBox=[rmin..rmax,-10..10,630..690]):
SZeiger:=plot::Line3d([r,-2,S(r)],[r,2,S(r)],r=rmin..rmax,
Tubular=TRUE, TubeDiameter=2):
scen3:=plot::Scene3d(hkeg3d,zyl3d, AnimationStyle=BackAndForth,
Header="2-Liter-Pokal",HeaderFont = ["arial", 16]):
scen4:=plot::Scene3d(SWand,SZeiger,AnimationStyle=BackAndForth,
Header="Silberverbrauch", HeaderFont = ["arial", 16]):
plot(scen3,scen4):