Extremwertaufgabe: Silberschmied
Prof. Dr. Dörte Haftendorn, MuPAD 4, Aug.06 Update
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Mathix ist Silberschmied geworden. Er möchte Pokale schmieden, bei denen auf eine Halbkugel ein offener Zylinder aufgesetzt ist. Er hat versucht auszurechnen, bei welchem Verhältnis von Zylinderhöhe und Radius er bei festem Volumen minimalen Silberverbrauch hat. Unten ist sein Rechenzettel. Schreiben Sie ihn kommentiert so auf, dass man die Schritte verstehen kann. Führen Sie ihn zuende und konkretisieren Sie für V= 2 Liter. Entwickeln Sie eine qualitative Skizze der Funktion S=S(r) aus Bausteinen. Warum sagt Mathilde: "Am besten lässt du den Zylinder weg." (Variante mit kegelförmigem Unterteil sie Extradatei)

Zielgröße: Silberverbrauch, entspricht der Oberfläche, setzt sich zusammen aus dem Zylindermantel und der Halbkugelfläche (hh=h, weil h später gebraucht wird):
Sformel:=2*PI*r*hh+2*PI*r^2;
![]()
Nebenbedingung, Volumen 2 Liter= 2000 cm^3, setzt sich zusammen aus Zylindervolumen und Halbkugelvolumen:
delete V:
NB:= V=PI*r^2*hh+2/3*PI*r^3;
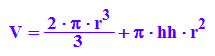
Nach r ließe sich diese Gleichung gar nicht leicht auflösen, daher Auflösen nach hh
assume(r>0): solve(NB,hh);
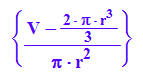
expand(-1/PI/r^2*(2/3*PI*r^3 - 2000))
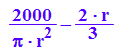
h:=r->V/(PI*r^2)-2/3*r;h(r);
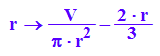
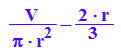
Nun wird das Volumen auf 2 Liter=2000cm^3 festgesetzt.
V:=2000: //Längen in cm
Aufstellen der Zielfunktion S in Abhängigkeit von r allein
S:=r->2*PI*r*h(r)+2*PI*r^2;S(r); expand(S(r)):
![]()
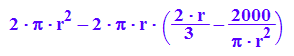
Man kann die Ausgabe markieren und in eine neue Ausgabezelle ziehen.
expand(2*PI*r^2 - 2*PI*r*(2/3*r - 2000/PI/r^2));
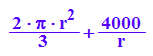
S:=r->2/3*PI*r^2 + 4000/r: S(r); //Zielfunktion
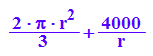
Aufbau der Zielfunktion aus Bausteinen:
plotfunc2d(4000/r,S(r),2*PI/3*r^2,r=0..16,
ViewingBoxYRange=0..1000 );
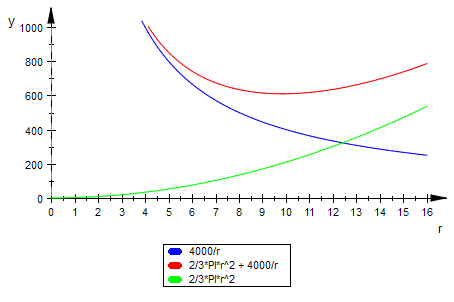
Als Summe aus Parabel und Hyperbel hat die Zielfunktion ein gesichertes Minimum, etwa bei r=10.
Berechnung:
S'(r);
solve(S'(r)=0,r)
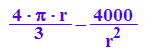
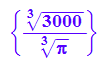
rs:=float(%[1])
![]()
Welches ist das maximale r, für welchel die 2 Liter ganz in der Halbkugel sind?
Wenn r noch größer würde, wäre der Pokal ja zu groß.
Berechnung aus dem Halbkugelvolumen:
rm:=(3*V/2/PI)^(1/3);rmf:=float(rm);
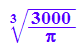
![]()
Da ergibt sich derselbe Wert, darum überrascht es nicht, wenn gilt:
simplify(h(rm))
![]()
Damit ist klar, dass Mathilde Recht hat, der Pokal für 2 Liter mit minimalem Silberverbrauch ist ein Halbkugel-Pokal ohne Zylinderrand. Die Silberoberfläche ist dann
simplify(S(rm));
float(%)
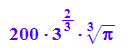
![]()
####################################################################
Herstellung der Graphen:
Sinnvolle optische Begrenzung für h könnte 10 sein. Wie groß ist dann r
solve(h(r)=rm,r)
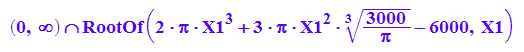
Exakt geht es nicht, also Ablesen:
plotfunc2d(h(r),10,r=-10..10,ViewingBoxYRange=0..12 )
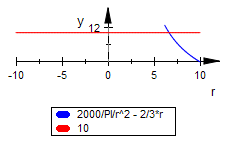
Numerische Bestimmung:
lo:=numeric::solve(h(r)=10,r);
lm:=numeric::solve(h(r)=0,r)
![]()
![]()
rmin:=lo[1];
rmax:=lm[1];
![]()
![]()
hkreis2d:=plot::Curve2d([r*cos(t),r*sin(t)],t=PI..2*PI,r=rmin..rmax);
zy2d1:=plot::Line2d([-r,0],[-r,h(r)],r=rmin..rmax ):
zy2d2:=plot::Line2d([r,0],[r,h(r)],r=rmin..rmax):
plot(hkreis2d,zy2d1,zy2d2,
ViewingBoxYRange=-rmax..10,LineWidth=1, Scaling=Constrained):
![]()
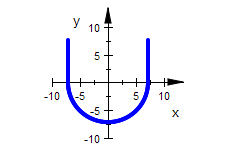

hkug3d:=plot::Surface([r*cos(t)*cos(phi),r*sin(t)*cos(phi),r*sin(phi)],
t=0..2*PI,phi=PI..2*PI , r=rmin..rmax);
zyl3d:=plot::Surface([r*cos(t),r*sin(t),hh],t=0..2*PI,hh=0..h(r),
r=rmin..rmax, ViewingBoxZRange=-rmax..10,
AnimationStyle=BackAndForth);
plot(hkug3d,zyl3d)
![]()
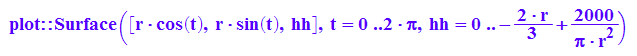
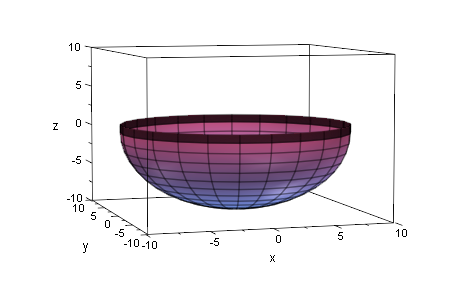

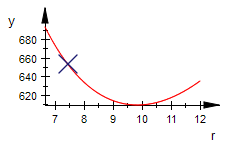
Darstellung der Zielfunktion allein und eines animierten Silververbrauchspunktes
Sg:=plot::Function2d(S(r),r=rmin..12, LineColor=[1,0,0]):
pkt:=plot::Point2d([r,S(r)],r=rmin..rmax+2, PointSize=5,
PointStyle=XCrosses):
plot(Sg,pkt);

Definition von Szenen, damit man alles zusammen sehen kann.
Leider können 2d- und 3d-Szenen micht in denselben plot.
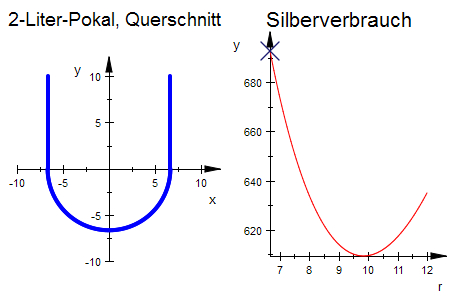
scen1:=plot::Scene2d(hkreis2d,zy2d1,zy2d2,
ViewingBoxYRange=-rmax..10,LineWidth=1,
AnimationStyle=BackAndForth,
Header="2-Liter-Pokal, Querschnitt",HeaderFont = ["arial", 14],
Scaling=Constrained):
scen2:=plot::Scene2d(Sg,pkt,AnimationStyle=BackAndForth,
Header="Silberverbrauch", HeaderFont = ["arial", 16]):
plot(scen1, scen2):

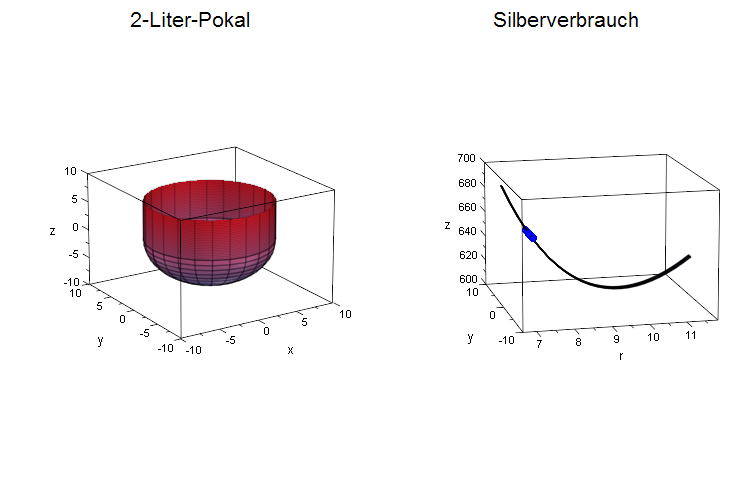
scen3:=plot::Scene3d(hkug3d,zyl3d, AnimationStyle=BackAndForth,
Header="2-Liter-Pokal",HeaderFont = ["arial", 16]):
SWand:=plot::Function3d(S(r),r=rmin..rmax+2,y=0..1,
ViewingBox=[rmin..rmax+2,-10..10,600..700]):
SZeiger:=plot::Line3d([r,-2,S(r)],[r,2,S(r)],r=rmin..rmax,
Tubular=TRUE, TubeDiameter=2):
scen4:=plot::Scene3d(SWand,SZeiger,AnimationStyle=BackAndForth,
Header="Silberverbrauch", HeaderFont = ["arial", 16]):
plot(scen3,scen4);