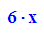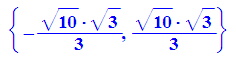fkt-gebrauch

Funktions-Gebrauch
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Mai. 06 Update 22.05.06
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben

Die beste Art, Funktionen zu definieren,
die zum mathematischen Vorgehen passt, ist die Funktionszuweisung.
Dabei soll zunächst der Parameter k einfach so im Term stehen

f:=x->x^3+k*x

f(x)

f(3)

f'(x)

f'(3)

f''(x)

f''(3)

xe:=solve(f'(x)=0,x)

f'(xe[1]),f'(xe[2])

f''(xe[1]),f''(xe[2])

float(f(xe[2]))

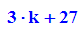
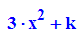
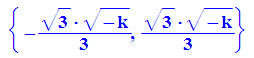
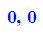
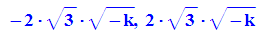
Für die Zeichnung gibt es mehrere Möglichkeiten für den Umgang mit k:
+++++++ Typ 1 ++++++++++
k festlegen

k:=1/2:
plotfunc2d(f(x),f'(x),f''(x));
delete k:

+++++++ Typ 2 ++++++++++
k zur Animation nutzen

plotfunc2d(f(x),f'(x),f''(x),x=-3..4,k=-2..2, ViewingBoxYRange=-5..10);

+++++++ Typ 3 ++++++++++
Schar mit Werten aufeinanderfolgenden Werten von k zeichnen

i^2+k $ i=1..5

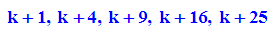
plotfunc2d(f(x)$ k=-2..2,x=-3..3, ViewingBoxYRange=-5..10)

+++++++ Typ 4 ++++++++++
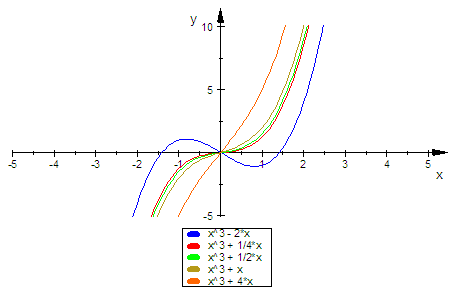
Schar mit ausgewählten Werten von k zeichnen.
Entweder den Term neu schreiben

plotfunc2d(x^3+k*x $ k in [-2,1/4,1/2,1,4], ViewingBoxYRange=-5..10)

oder k substituieren

subs(f(k,x), x = 7)

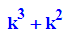
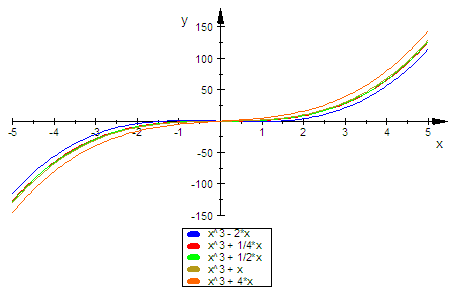
alle:=subs(f(x),k=kk) $ kk in [-2,1/4,1/2,1,4]

plotfunc2d(alle)

f(x)

plotfunc3d(f(x))

########################################################
Die beste Art, Funktionen zu definieren,
die zum mathematischen Vorgehen passt, ist die Funktionszuweisung.
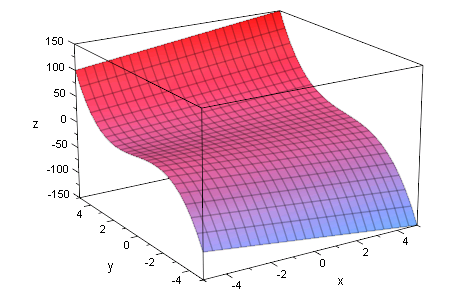
Dabei soll nun der Parameter k als zweite Variable auftreten.

fk:=(k,x)->x^3+k*x+1

fk(k,x)

diff(fk(k,x),x)

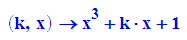
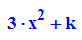
plotfunc2d(fk(1,x),diff(fk(10,x),x))

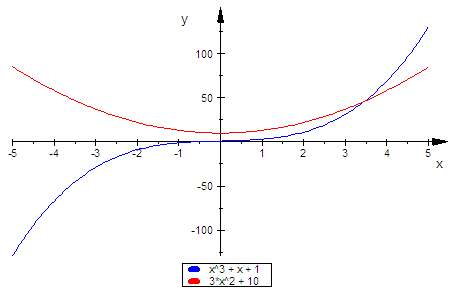
Zweite Ableitung nach x

diff(fk(k,x),x,x)

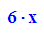
Damit man die Ableitung nun auch als Funktion hat,
verwendet man fp::unapply

diff(fk(k,3),x)

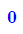
ffk:=fp::unapply(diff(fk(k,x),x))

ffk(k,a+b)

ffk(k^2+1,a+b)

ff(5,x)

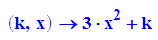
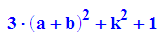
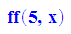
solve(diff(fk(k,x),x)=0,x)

solve(ffk(k,x)=0,x)

########################################
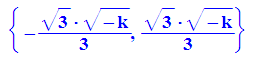
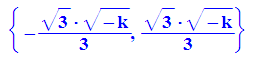
Funktionen zusammensetzen:
Man kann Funktionen als Zuordnung x-> Funktionsterm definieren,
aber auch durch Verwendung von Funktionsnamen anderer Funktionen.
Terme aus Funktionsnamen heißen "Funktionale Terme", (Term=Ausdruck=expression)

g:=x->3*sin(2*x):
h:=x->PI*x^2:
s:=g+h;
f:=x->g(h(x));
k:=g@h;

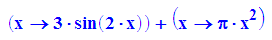
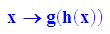
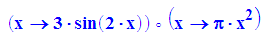
g(x);h(x);s(x); f(x); k(x)

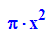
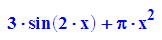
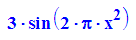
plotfunc2d(g(x),h(x),s(x),f(x))

s;
s(x)

ss:=sin+6*sin+h

ss(x)

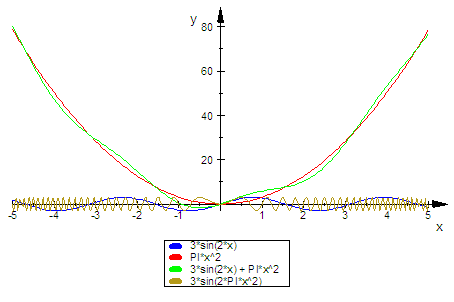
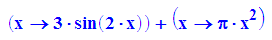
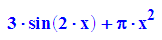
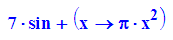
Nun kann man auch funktionale Terme aus Ausrücken gewinnen

sse:=fp::expr_unapply(ss(x))

sse(x)

plotfunc2d(sse(x),2*sin(x),PI*x^2,ss(x), LineWidth=0.7)

####################################
Nicht so empfehlenswert ist, nur die Terme zu verwenden,
da man keine Einsetzungen einfach machen kann.
Möglich aber ist es.

ft:=1/10*x^3-x

plotfunc2d(ft)

ff:=diff(ft, x)

subs(ff, x =5)

xe:=solve(ff=0,x)

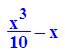
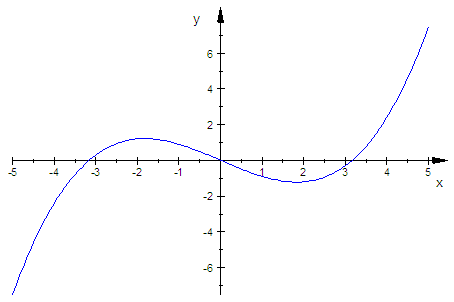
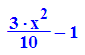
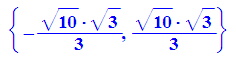
Bei der Verwendung der Lösungamenge passiert Unsinn:

subs(ft, x =xe)

xe[1]

subs(ft,x=xe[1])

li:={1,2,10}

1/10*x^3-x $ x in li

ft:=(1/10*x^3-x)

ft $ x in li

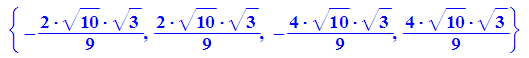
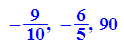
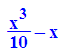
Error: Wrong number of arguments [_power]

Dieses hätte nicht passieren dürfen, eine Email an MuPAD ist unterwegs.