pZ:=x->2/5*(x+2)*(x-1);
pN:=x->(x-2);
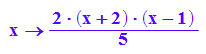
![]()
Gebrochenrationale Funktionen LEVEL 1, Grundlagen
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Mai 07
Analysis mit MuPAD 4,
Automatische Übersetzung aus MuPAD 3.11, Okt. 05 Version vom Jul.06 update Aug06
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Definition: Funktionen, die sich als Quotienten aus zwei Polynomen darstellen lassen,
heißen gebrochenrationale Funktionen.
Beispiel LEVEL 1 gekürzter Term, schräge Asymptote
Beispiel LEVEL 2 ungekürzter Term, stetige Fortsetzung
Beispiel LEVEL 3 aufwendigerer Funktionstem, mehrere Pole
#################################################################
Beispiel LEVEL 1
Diese Seite ist so gestaltet, das man durch Eintrag anderer Zähler- und Nennerpolynome
ohne weiteres Zutun (mit Evaluiere->alle Eingaben) etliche der schulischen Aufgaben
durchführen kann.
pZ:=x->2/5*(x+2)*(x-1);
pN:=x->(x-2);
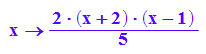
![]()
//pZ:=x->2/5*(x+2)*(x-1);pN:=x->(x-2);
//dies war die Aufgabe, zu der der Test genau passt
f:=x->pZ(x)/pN(x); f(x)
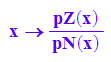
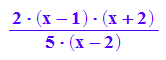
Sofort erkennbar sind die beiden Nullstellen bei x=1 und x=-2
und die Polstelle x=2, Pol mit Zeichenwechsel.
Wegen des Grad-Unterschiedes 1 muss es eine schräge Asymptote geben.
plotfunc2d(f(x))
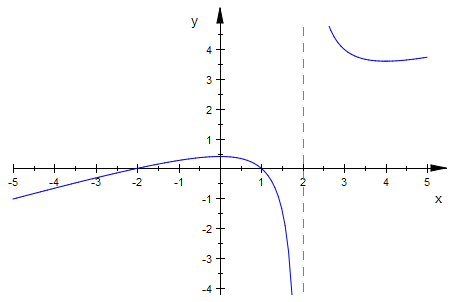
So war die Erwartung.
Man hätte sich den Graphen auch aus zwei Bausteinen aufbauen können:
Damit kann man den qualitativen Graphen gut begründen.
plotfunc2d(f(x),pZ(x),pN(x))
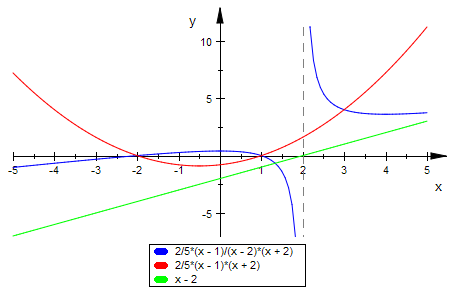
Zusamenhänge:
Wo der Zähler 0 ist hat f Nullstellen, wenn der Nenner dort ungleich 0 ist.
Wo der Nenner 0 ist hat f Polstellen,wenn der Zähler dort ungleich 0 ist.
Wo der Nenner 1 ist, schneidet f den Zählergraphen.
Wo der Zähler 1 ist, hat f den Kehrwert des Nennerwertes, wenn der Nenner dort ungleich 0 ist.
Haben Zähler und Nenner gleichen Grad, gibt es eine waagerechte Asymptote.
Ist der Nennergrad größer als der Zählergrad, ist die x-Achse Asymptote.
Ist der Zählergrad größer als der Nennergrad, gibt es eine Polynom-Asymptote, deren Grad die
Differenz aus Zählergrad und Nennergrad ist.
+++++++++++++++++
Beschaffung der Asymptoten
teile:=divide(pZ(x),pN(x))
![]()
MuPAD liefert "Ganzrationer Anteil, Rest".
So wie 60:7=8+ 4/7 <==> 60= 8*7+4
muss man das jetzt deuten.
hold(f(x)=teile[1]+teile[2]/pN(x));
f(x)=teile[1]+teile[2]/pN(x)
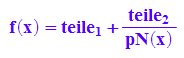
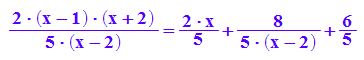
So wie der "Rest" immer kleiner als der Teiler ist,
ist die "Restfunktion" immer im Grad kleiner als das
Nennerpolynom.
++++++++++++++++++++++++++++
asy:=x->teile[1];asy(x);
g:=x->teile[2]/pN(x);g(x);
![]()
![]()
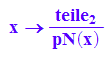
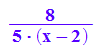
Probe
probe:=asy(x)+g(x)
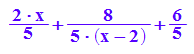
simplify(f(x)-probe)
![]()
++++++++++++++++++++++++++
Einzeichnen der Asymptote und des Restes:
plotfunc2d(f(x),asy(x),g(x))
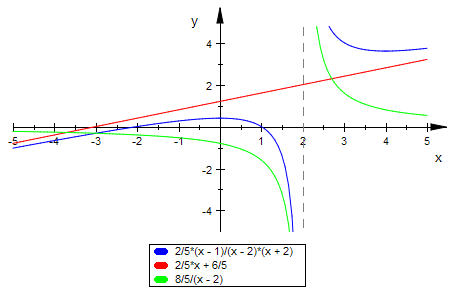
Man kann sich vorstellen, dass die x-Achse gedreht wird, bis sie die Lage der
Asymptote hat. Dabei wird die einfache grüne Hyperbel mit gedreht und man
erhält den gesuchten Graphen von f.
Allgemein hat die "Restfunktion" immer die x-Achse als Asymptote und wird auf die
Asymptote aufgesetzt.
Das stimmt auch für Asymptoten-Paraben u.s.w.
++++++++++++++++++++++++++
Beschaffung der Extrema, die man hier mit Sicherheit erwartet.
Anmerkung für Puristen: Was heißt hier "mit Sicherheit"?
Schulisch - und im besten Sinne mathematisch- ist eine umfassendes Sicht
auf die Phänomene sinnvoll. Dazu gehört ein "umrundendes" Vorgehen mit passenden
Wechseln der Aspekte. Das heißt hier: der Graph zeigt eindeutige Extrema, weder kann es mehr noch kann es weniger Extrema geben, wie die Sicht auf die Bausteine zeigt.
Irgendwelche Unsicherheiten bei den Lernenden zu erzeugen, in dem man so tut, als sei das alles nicht sicher, bevor man nicht die 2. Ableitung untersucht, sind mathematischer und pädagodischer Unsinn.
Viel sinnvoller sind Klassifizierungs-Überlegungen: Welche Fälle können beim Typ "Parabel durch Gerade"
überhaupt auftreten. Damit wird sehr viel mehr Eigentätigkeit ermöglicht und sehr viel besser
Mathematik gelernt.
+++++++++++++++++
Weitere Untersuchungen
ableitung:=asy'(x)+g'(x)
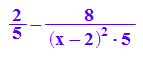
Anmerkung: i.A. ist dies leichter zu berechnen als f'(x), allerdings muss man für die
Nullstellen der Ableitung nun auf der Hauptnenner bringen, wenn man "von Hand" arbeitet.
Mit dem CAS ist es egal.
ex:=solve(ableitung=0,x)
![]()
Sollte hier in anderen Fällen "RootOf" stehen, muss man numerisch vorgehen. Siehe LEVEL 3
f(x) $ x in ex // Ordinaten der Extrema
![]()
float(f(x)) $ x in ex // Ordinaten der Extrema
![]()
####################################################################