pZ:=x->(x+3)*(x-1);
pN:=x->(x^2-1);
![]()
![]()
Gebrochenrationale Funktionen LEVEL 2
ungekürzter Term, stetige Fortsetzung
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Mai 07
Analysis mit MuPAD 4,
Automatische Übersetzung aus MuPAD 3.11, Okt. 05 Version vom Jul.06 update Aug06
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Beispiel LEVEL 1 gekürzter Term, schräge Asymptote
Beispiel LEVEL 2 ungekürzter Term, stetige Fortsetzung Dies ist diese Seite.
Beispiel LEVEL 3 aufwendigerer Funktionstem, mehrere Pole
#################################################################
Beispiel LEVEL 2
Diese Seite ist kann man für ähnliche Beispiele leicht anpassen.
Dabei muss man vor allem die Lücke x=1 passend ersetzen.
pZ:=x->(x+3)*(x-1);
pN:=x->(x^2-1);
![]()
![]()
//pZ:=x->(x+3)*(x-1);pN:=x->(x^2-1);
//dies war die Aufgabe, zu der der Test genau passt
f:=x->pZ(x)/pN(x); f(x)
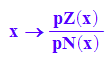
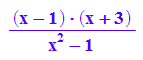
Sofort erkennbar sind die beiden Nullstellen des Zählers bei x=1 und x=-3
und die Nullstellen des Nenners bei x=1 und x= -1.
Aha!!!!!! Zähler und Nenner haben eine gemeinsame Nullstelle.
Zerlegt man Zähler und Nenner in Faktoren (3. binomische Formel hier), dann sieht man das noch besser.
factor(pZ(x)),factor(pN(x))
![]()
Der Definitionsbereich von f ist 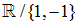
nichtDef:=discont(f(x),x)
![]()
Das wird von MuPAD richtig erkannt.
Allerdings wird sofort gekürzt, wenn die gleiche Linearfaktoren
schon sichtbar sind.
Hier lässt sich der der gemeinsame Linearfaktor vollständig kürzen.
Andere Fälle werden in LEVEL 3 behandelt.
ff:=x->(pZ(x)/factor(pN(x)));
ff(x);
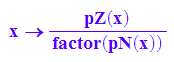
![]()
Hier ist ff(1) dennoch nicht nicht bestimmbar. Das ist mathematisch korrekt.
//ff(1)
Das heißt MuPAD behält den ursprünglichen Definitionsbereich bei.
Also definieren wir:
luecke:=1:
fs:=x->(x+3)/(x+1)
![]()
fs(luecke)
![]()
Man nennt die Funktion fs die "stetige Forsetzung von f".
f und fs unterscheiden sich nur im Definitionsbereich.
Hier hat fs hat den Definitionsbereich 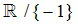
Die Graphen von f und fs sehen fast gleich aus, nur hat f an der Stelle x=luecke
eine sogenannte "hebbare Unstetigkeitsstelle", ein "Lücke".
Genaueres zur Stetigheit siehe unten ****.
grf:=plot::Function2d(f(x),x=-4..3,
LineColor=RGB::Red, LineStyle=Dashed, LineWidth=1):
grfs:=plot::Function2d(fs(x),x=-5..5,
LineColor=RGB::Blue):
grluecke:=plot::Point2d([luecke,fs(luecke)],PointSize=3, PointStyle=Circles):
plot(grf,grfs, grluecke);
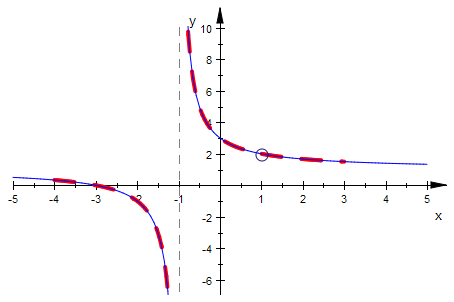
Für alle weiteren Untersuchungen kann man die stetige Fortsetzung fs
anstelle von f nehmen.
++++++++++++
Man sieht sofort, wenn man sich große x eingesetzt denkt, dass y=1 eine waagerechte
Asymptote ist.
Bestimmung mit MuPAD:
limit(fs(x),x=infinity)
![]()
Alterativ
teile:=divide(pZ(x),pN(x))
![]()
teile[1]+factor(teile[2]/factor(pN(x)))
![]()
Alternativ mit "Hinsehen"
(x+3)/(x+1),(x+1+2)/(x+1),1+2/(x+1)
![]()
Es handelt sich also um eine gewöhnliche Hyperbel, mit Steckfaktor 2,
die um 1 nach oben und 1 nach links geschoben ist. f hat dazu bei
x=1 eine Lücke, die durch den Wert 2 geschlossen werden kann.
Der Pol mit Zeichenwechsel bei x=-1 ist davon nicht betroffen.
Man kann dieses Schließen der Lücke auch "augenfällig" machen:
fst:=x->piecewise([x<>1,f(x)],[x=luecke,fs(x)]);
fst(x)
![]()
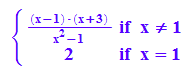
plotfunc2d(1,fst(x))
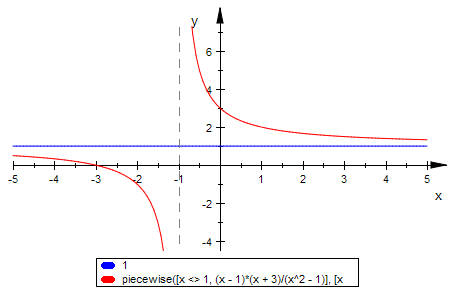
"Unstetigkeitsstelle"
Die Definition der Stetigkeit bezieht sich ausschließlich auf Stellen x=a aus dem
Definitionsbereich einer Funktion.
x=1 liegt nicht im Definitionsbereich von f.
f ist stetig in seinem Definitionsbereich. Insofern ist x=1 eine Definitionslücke,
die "stetig geschlossen werden kann".
Der Begriff "Stetig schließbare Definitionslücke" wäre als besser als
"hebbare Unstetigkeitsstelle".
funstet:=x->piecewise([x<>luecke,f(x)],[x=luecke,fs(x)+1])
![]()
Wenn man dagegen die Lücke durch einen "falschen" Wert füllt,
limit(fs(x),x=1);
funstet(1)
![]()
![]()
dann hat man tatsächsich bei x=1 eine Unstetigkeitsstelle. f ist unstetig für x=1.
Jetzt gehört 1 nämlich zum Def.bereich, der Funktionswert 3 kann aber durch Grenzwertbildung
nicht erreicht werden. (Lies nochmal die Definition der Stetigkeit.)
Nun ist x=1 erst wirklich eine hebbare Unstetigkeitsstelle.
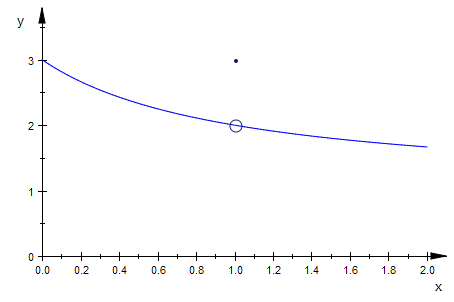
fug:=plot::Function2d(funstet(x),x=0..2,ViewingBoxYRange=0..3.5):
pkt:=plot::Point2d([1,funstet(1)],PointSize=1):
plot(fug,pkt,grluecke);
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
limit(funstet(1+h),h=+0);
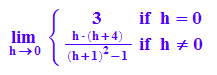
limit( h/((h + 1)^2 - 1)*(h + 4),h=0)
![]()
In dieser Stetigkeitsüberprüfung mit h->0 muss man den unteren Term getrennt betrachten.
Bemerkenswerterweise wäre dies von Hand auch gegengen mit Klammerauflösen und h Kürzen
oder mit der Regel vom l'Hopital.