//weitere Terme ohne (x-1) können auch da sein.
pZ:=x->(x-1)^m;
pN:=x->(x-1)^n;
![]()
![]()
Gebrochenrationale Funktionen LEVEL 3
Aufwändigerer Term, evt. mehrere Pole
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Mai 07
Analysis mit MuPAD 4,
Automatische Übersetzung aus MuPAD 3.11, Okt. 05 Version vom Jul.06 update Aug06
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Beispiel LEVEL 1 gekürzter Term, schräge Asymptote
Beispiel LEVEL 2 ungekürzter Term, stetige Fortsetzung
Beispiel LEVEL 3 aufwendigerer Funktionsterm, e.v.t. mehrere Pole Diese Seite.
Fall1 Gemeinsame Nullstelle höherer Vielfachheit in Zähler und Nenner
Fall2 Keine gemeinsame Nullstelle, aber Nennernullstellen höherer Vielfachheit
#################################################################
Diese Seite ist kann man für ähnliche Beispiele leicht anpassen.
Fall 1 ------------------------------------------
Gemeinsame Nullstelle in Zähler und Nenner
Vielfachheit m>0 und n>0
//weitere Terme ohne (x-1) können auch da sein.
pZ:=x->(x-1)^m;
pN:=x->(x-1)^n;
![]()
![]()
//pZ:=x->(x-1)^m;pN:=x->(x-1)^n;
//dies war die Aufgabe, zu der der Test genau passt
f:=x->pZ(x)/pN(x); f(x)
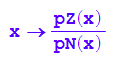
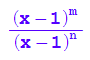
Jedenfalls gehört 1 nicht zum Definitionsbereich.
Fall 1 a) m=n Man kann vollständig kürzen. Bei x=1 ist eine hebbare Unstetigkeitsstelle.
Fall 1 b) m>n Man kann den Nenner vollständig wegkürzen.
Bei x=1 ist eine hebbare Unstetigkeitsstelle. Die stetige Fortsetzung hat eine Nullstelle
der Vielfachheit m-n. (Begriffe siehe LEVEL 2)
Fall 1c) m<n Man kann den Zähler vollständig wegkürzen.
Bei x=1 ist eine Polstelle vom Grad n-m. (Siehe unten Fall 2)
+++++++++++++++++++++++++++++++++++++++++++++
Beispiel 1b):
pZ1b:=x->(x-1)^4*(x+6);
pN1b:=x->(x-1)^2*(x-4);
f1b:=x->pZ1b(x)/pN1b(x);
f1b(x);
![]()
![]()

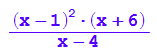
plotfunc2d(f1b(x),x=-10..10)
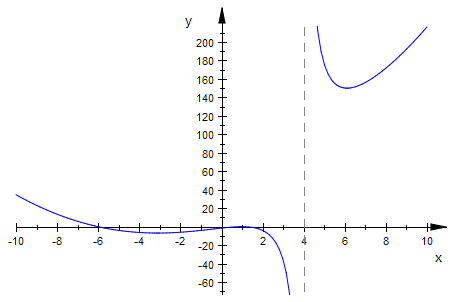
Zu erwarten ist eine Parabel-Asymptote, da Zählergrad-Nennergrad=5-3=3-1=2 ist
teile:=divide(pZ1b(x),pN1b(x))
![]()
teile[1]
![]()
plotfunc2d(f1b(x),teile[1],x=-10..10)
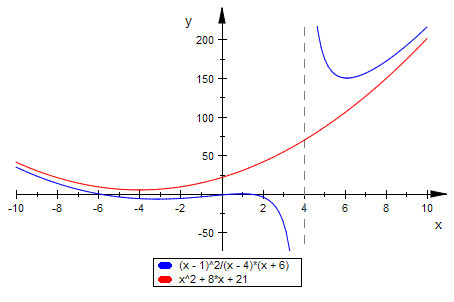
Der wahre "Rest" ist übrigens 90, denn:
divide(teile[2],(x-1)^2)
![]()
Probe, die stetige Fortsetzung als Parabel+Hyperbel
probe:=teile[1]+90/(x-4)
![]()
simplify(probe-f1b(x))
![]()
+++++++++++++++++++++++++++++++++++++++++++++
Beispiel 1c):
pZ1c:=x->(x-1)^2*(x+3);
pN1c:=x->(x-1)^4*(x-2);
f1c:=x->pZ1c(x)/pN1c(x);
f1c(x);
![]()
![]()

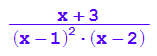
plotfunc2d(f1c(x))
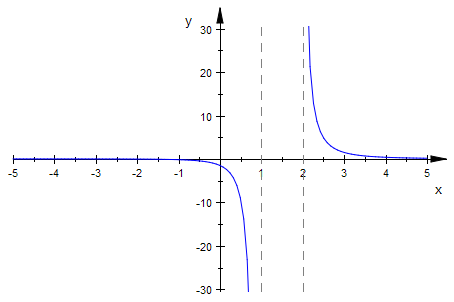
Links ist bei x= - 3 ist noch eine Nullstelle zu erwarten. (wegen (x+3)-Faktor).
Die x-Achse ist Asymptote, da der Nennergrad größer als der Zählergrad ist.
plotfunc2d(f1c(x),x=-10..-2)
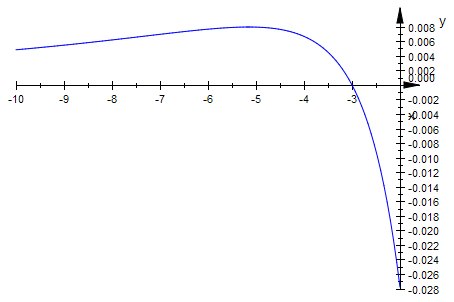
#################################################################
Fall 2 ------------------------------------------
Keine gemeinsame Nullstelle, aber Nennernullstellen höherer
Vielfachheit
f2k:=x->1/(x-1)^k
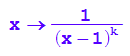
Definition Eine Polstelle x=a hat den Grad k, wenn im gekürzten Term der
Nenner eine Nullstelle vom Grad k (= Vielfachheit k) , also den Faktor (x-a)^k hat.
Man sagt auch "f hat bei x=a einen Pol vom Grad k".
alle:=f2k(x)$ k=1..7
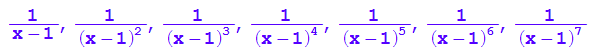
plotfunc2d(alle,x=-2..3,ViewingBoxYRange=-3..3)
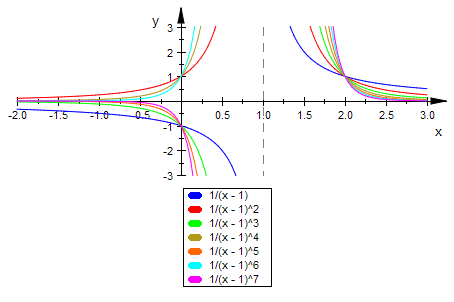
Fazit:
Ist k ungerade, so handelt es sich um einn Pol mit Vorzeichenwechsel.
Ist k gerade, so handelt es sich um einn Pol ohne Vorzeichenwechsel.
Jeder Linearfaktor (des gekürzten Terms) in Zähler und Nenner hat seinen vorhersagbaren
Einfluss.
pZ2:=x->(x-1)^2*(x+2);
pN2:=x->(x+1)^2*(x-2)^3;
f2:=x->pZ2(x)/pN2(x);
f2(x);
plotfunc2d(f2(x),x=-5..5,ViewingBoxYRange=-1..1)
![]()
![]()
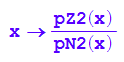
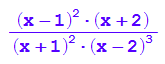
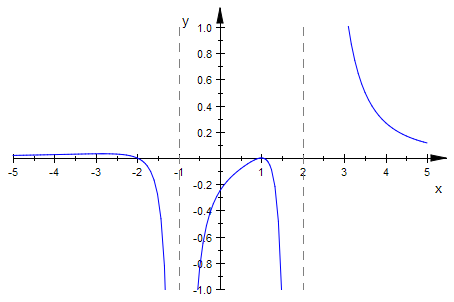
Also konnte man vorhersagen:
Eine einfache Nullstelle bei x=-2, ein Pol ohne Zeichenwechsel bei x=-1,
eine Berühr-Nullstelle bei x=1, ein Pol mit Zeichenwechsel bei x=2.