start:=1:
werte:=start,(hanoi@@i)(start) $ i=1..4;
![]()
Iteration-Rekursion allgemein
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Okt. 05 Update 19.4.07
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
####################################################
Turm von Hanoi, allgemeine Erläuterung (diese Seite)
Heronverfahren zum Wurzelziehen (diese Seite)
Newtonverfahren (diese Seite)
Logistische Parabel (extra Seite)
####################################################
Kern der Iteration ist die Anwendung einer Funktion auf ihre eigene
Ausgabe, in MuPAD erzeugt durch @@
(f@@n)(start) wendet f auf start an, und dann f auf das Ergebnis, usw.
insgesamt n mal.
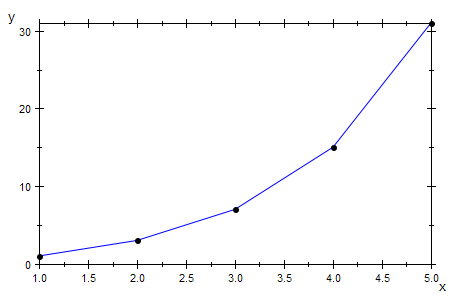
hanoi:=x->(2*x+1): //Trägerfunktion der Iteration
start:=1:
werte:=start,(hanoi@@i)(start) $ i=1..4;
![]()
Der Startwert start wird auf 1 gesetzt. Der Doppelpunkt unterdrückt die Ausgabe.
Mit start, wird der Wert dann doch angezeigt und zwar, wegen des Kommas als erster Wert einer Folge.
Der eigentliche Teil der Folge wird dann erzeugt.
$ heißt Folgengerator, der Laufindex i läuft von 1 bis 4.
Der vor $ stehende Term wird also mit Werten 1=,i=2,.. ausgewertet.
Es entstehen die Werte (hanoi@@1)(x), (hanoi@@2)(x), ...,
das ist ausführlich hanoi(start), hanoi(hanoi(start)), hanoi(hanoi(hanoi(start)),..
// sind Zeilen-Kommentare
Graphen dazu auf zwei Arten: "Zeit-Graphen" und "Spinnweb-Graphen"
grwerte:=plot::Listplot([werte]):
plot(grwerte);
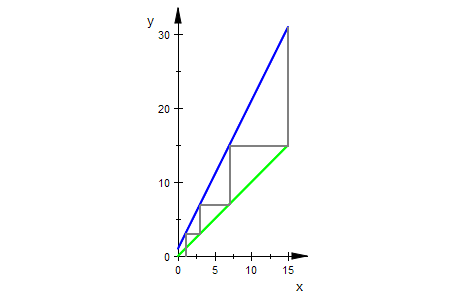
it:=plot::Iteration(hanoi(x),start, x = 0..15,
LineStyle=Solid, LineWidth=0.65):
wh:= plot::Function2d(x, x = 0..15,LineWidth=0.6, Color=RGB::Green):
ghanoi:= plot::Function2d(hanoi(x), x = 0..15, LineWidth=0.6):
plot(wh,ghanoi, it)
############################################
Heronfolge zur Quadrat-Wurzelberechnung
heron:=x->((x+a/x)/2): heron(x); //Berechnung von Wurzel(a)
![]()
a:=2: start:=0.1:
werte:=start,float((heron@@i)(start)) $ i=1..6; //Wurzel(2)
![]()
float(wert) gibt wert als Dezimalzahl oder mit Hilfe von Dezimaleahlen aus.
a2:=100:start2:=1:start2,float((heron@@i)(start2)) $ i=1..7;
![]()
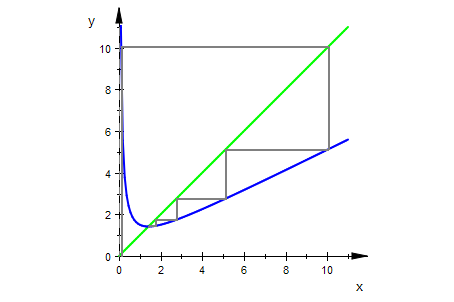
Das Heronverfahren funktioniert sogar, wenn man "blind" startet.
it:=plot::Iteration(heron(x),start, x = 0..11,
LineStyle=Solid, LineWidth=0.65):
wh:= plot::Function2d(x, x = 0..11,LineWidth=0.6, Color=RGB::Green):
gheron:= plot::Function2d(heron(x), x = 0..11, LineWidth=0.6):
plot(wh,gheron, it)
############################################
Newtonverfahren zur Nullstellenbestimmung
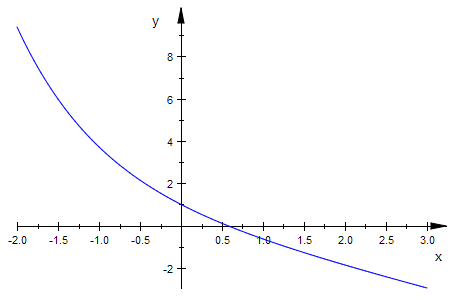
f:=x->(E^(-x)-x): f(x);
![]()
plotfunc2d(f(x),x=-2..3)
newt:=x->(x- f(x)/f'(x)); normal(newt(x));
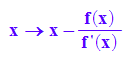
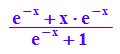
start:=3: start, float((newt@@i)(start)) $ i=1..4;
![]()
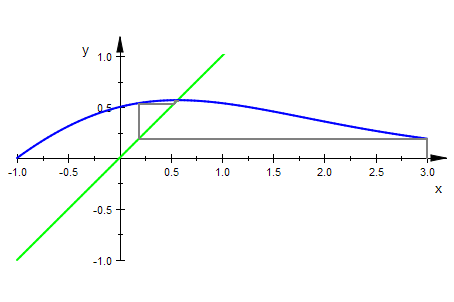
it:=plot::Iteration(newt(x),start, x = -1..3,
LineStyle=Solid, LineWidth=0.65):
wh:= plot::Function2d(x, x = -1..3,ViewingBoxYRange=-1..1,
LineWidth=0.6, Color=RGB::Green):
gnewt:= plot::Function2d(newt(x),x = -1..3, LineWidth=0.6):
plot(wh,gnewt, it)
delete f,newt:
newt:=x->x-f(x)/f'(x)
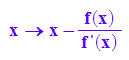
Fixpunkt liegt bei x mit f(x)=0, also bei der gesuchten Nullstelle.
Steigung im Fixpunkt xs:
newt'(x)
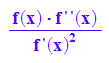
Ist f(xs)=0 aber nicht auch f'(xs)=0 auch nicht f'(xs)=unendlich,
dann fällt der mittlere Term weg und der vordere kürzt sich zu 1.
Also ist newt'(xs)=0.
Also schneidet die Newtonfunktion die Winkelhalbierende (i.a.) waagerecht.
Man sagt: das Newtonverfahren konvergiert "superschnell".
//-----------------------------------------
Anderenfalls ist der Grenzwert von 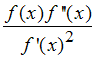
mit der Regel von de L'Hospital zu bilden.
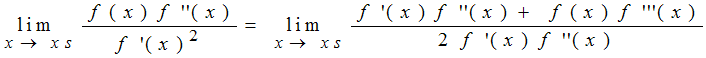
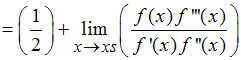
Wenn der letzte Grenzwert nun 0 ist, ist die Steigung im Fixpunkt immerhin 1/2.
Damit konvergiert das Newtonverfahren wenigstens noch linear.