f:=x->(x-1)^2-1
![]()
Integrale- Lerndatei
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11, Aug. 05 Update Sept.05
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1. Grundlagen rechnen und zeichnen ###
2. Riemann-Summen ### 3. Zwischenflächen ###
f:=x->(x-1)^2-1
![]()
Unbestimmtes Integral
int(f(x), x)
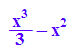
Bestimmtes Integral
int(f(x),x=2..4)
![]()
Um die vom Integral berechnete gewichtete Fläche zu bestimmen,
müssen verschiedenartige Graphik-Elemente kombiniert werden.
Sie heißen "Graphik-Primitive", siehe Graphen-Lerndatei, Level 2.
gf:=plot::Function2d(f(x),x=-1..4,
Color=RGB::Red, LineWidth=1):
igf:=plot::Integral(gf):
plot(igf,gf)
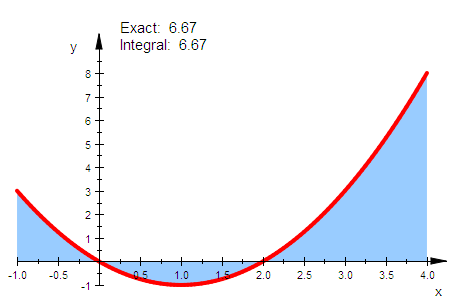
Der Befehl plot::Integral bekommt also die eine Graphik-Primitive der Funktion
f übergeben.
Für Integrale, deren Intervall nicht das Darstellungsintervall ist, muss man einen
kurzen Graphen in dem Intergrationsintervall erzeugen.
gfklein:=plot::Function2d(f(x),x=2.5..3.5):
igfklein:=plot::Integral(gfklein):
plot(igfklein,gf)
2. Riemann-Summen ##################
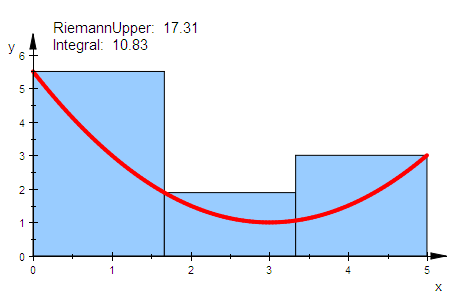
Zur Unterstützung von Unterricht gibt es eine einfache Art,
Riemannsche Untersummen und Obersummen darzustellen.
Das wird durch eine Option in dem plot::Integral -Befehl erreicht.
Die 3 in dem Befehl steht für 3 Streifen.
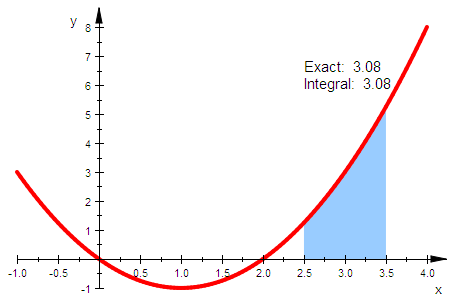
p:=x->1/2*(x-3)^2+1
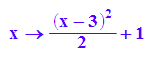
gp:=plot::Function2d(p(x),x=0..5,
Color=RGB::Red, LineWidth=1):
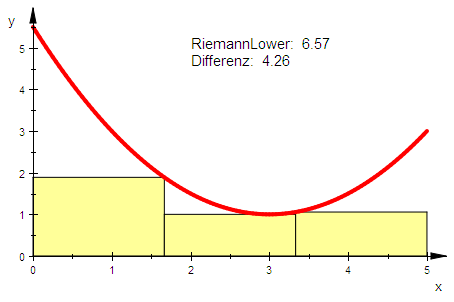
igprl:=plot::Integral(gp,3,IntMethod=RiemannLower,
Color=RGB::LightYellow,ShowInfo =
[IntMethod = "RiemannLower",
Error = "Differenz",Position=[2,4.5]]):
igpru:=plot::Integral(gp,3,IntMethod=RiemannUpper):
plot(igpru,gp);plot(igprl,gp);
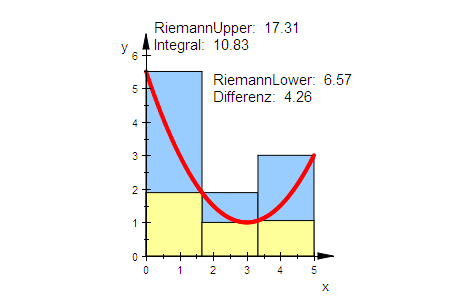
plot(igpru,igprl,gp,Scaling=Constrained);
3. Zwischenflächen ############################
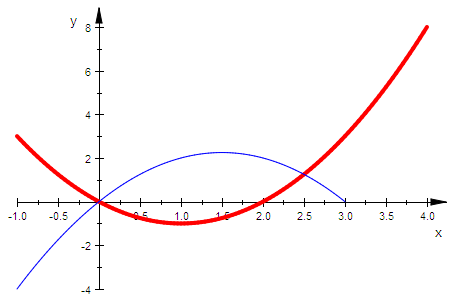
h:=x->x*(3-x);
![]()
gh:=plot::Function2d(h(x),x=-1..3):
plot(gf,gh)
Erst braucht man wieder Graphik-Primitive der beteiligten Funktionen.
Dann muss in vielen Aufgaben erst noch die Schnittstelle berechnet werden:
lo:=solve(f(x)=h(x))
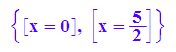
lo2:=(lo[2])[1]
![]()
xs:=subs(x, lo2)
![]()
Hier wurde die Lösung herausgriffen und getauft, damit sie nicht von
Hand übertragen werden muss.
zwisch:=plot::Hatch(gf,gh,0..xs)
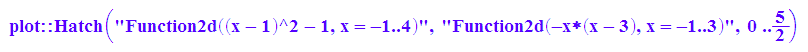
plot(zwisch,gf,gh)
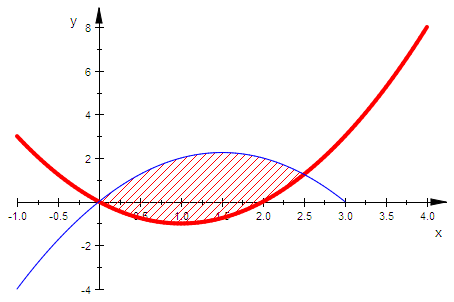
Berechnung der Zwischenfläche
int(h(x)-f(x),x=0..5/2); float(%);
![]()
![]()