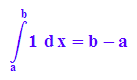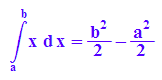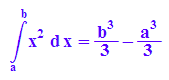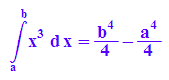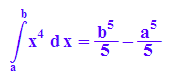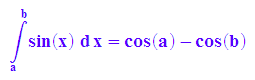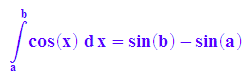f:=x->x^2
![]()
Integration der Normalparabel
Prof. Dr. Dörte Haftendorn, MuPAD 4, https://mathe.web.leuphana.de Aug.06
Automatische Übersetzung aus MuPAD 3.11,Juni 06 Update 21.06.06
Es fehlen noch textliche Änderungen, die MuPAD 4 direkt berücksichtigen, das ist in Arbeit.
Web: https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
f:=x->x^2
![]()
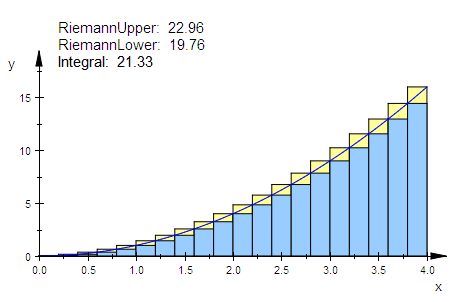
summen:=student::plotRiemann(f(x),x=0..4,10):plot(summen)
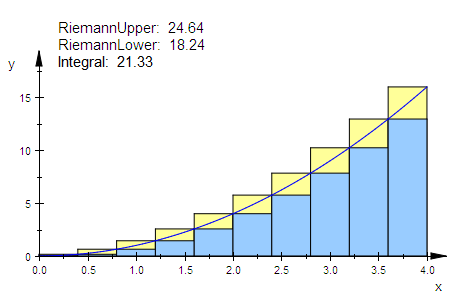
summen:=student::plotRiemann(f(x),x=0..4,20):
plot(summen)
summen:=student::plotRiemann(f(x),x=0..4,50):
plot(summen)
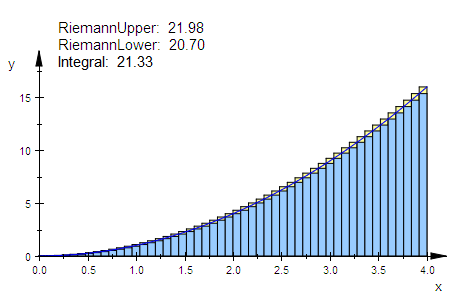
Bildung der Unter- und Obersumme
sum(i^2, i=1..n)
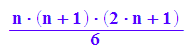
sum(i^2, i=1..n-1)
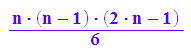
untersumme:=b^3/n^3*sum(i^2, i=0..n-1)
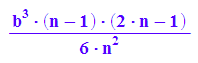
obersumme:=b^3/n^3*sum(i^2, i=1..n)
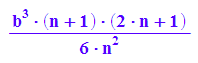
limit(expand(untersumme), n=infinity)
![]()
limit(expand(obersumme), n=infinity)
![]()
Da Unter- und Obersummen gegen denselben Wert konvergieren,
existiert das Integral und ist gleich diesem Wert.
hold(int(x^2,x=0..b))=int(f(x), x=0..b)
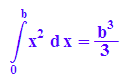
Auch die Summen kann man symbolisch erhalten:
student::riemann(f(x),x=0..4,4, Left );float(%);
student::riemann(f(x),x=0..4,4 );float(%);
student::riemann(f(x),x=0..4,4, Right );float(%);
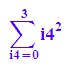
![]()
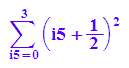
![]()
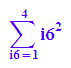
![]()
float(student::riemann(f(x),x=0..4,4*n )) $ n=1..5;
![]()
float(int(f(x), x=0..4))
![]()
#############################################
bestimmtes Intergal über x^2 von a bis b
hold(int(x^2,x=a..b))=int(x^2, x=a..b)
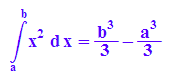
Das Entsprechende für andere Funktionen:
hold(int(1,x=a..b))=int(1, x=a..b);
hold(int(x,x=a..b))=int(x, x=a..b);
hold(int(x^2,x=a..b))=int(x^2, x=a..b);
hold(int(x^3,x=a..b))=int(x^3, x=a..b);
hold(int(x^4,x=a..b))=int(x^4, x=a..b);
hold(int(sin(x),x=a..b))=int(sin(x), x=a..b);
hold(int(cos(x),x=a..b))=int(cos(x), x=a..b);