hold(int(k*f(x), x))=int(k*f(x), x);
hold(int(f(x)+g(x), x))=int(f(x)+g(x), x);
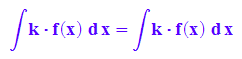
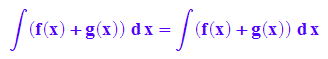
Integrationsregeln
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4, Aug. 06 Update Jan 08
https://mathe.web.leuphana.de www.mathematik-verstehen.de
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
hold sorgt dafür, dass die Formeln angezeigt, aber nicht berechnet werden.
hold(int(k*f(x), x))=int(k*f(x), x);
hold(int(f(x)+g(x), x))=int(f(x)+g(x), x);
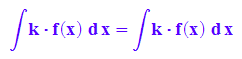
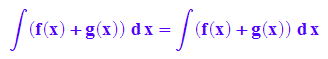
Bei den folgenden Formeln wird auf der rechten Seite
von MuPAD wirklich die unbestimmte Integration durchgeführt.
hold(int(1,x))=int(1, x);
hold(int(x,x))=int(x, x);
hold(int(x^2,x))=int(x^2, x);
hold(int(x^3,x))=int(x^3, x);
hold(int(x^4,x))=int(x^4, x);
hold(int(sin(x),x))=int(sin(x), x);
hold(int(cos(x),x))=int(cos(x), x);
hold(int(tan(x),x))=int(tan(x), x);
hold(int(exp(x),x))=int(exp(x), x);
hold(int(ln(x),x))=int(ln(x), x);
hold(int(1/x,x))=int(1/x, x);
hold(int(1/x^k,x))=int(1/x^k, x);
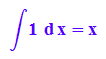
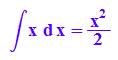
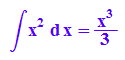
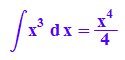
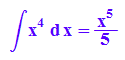
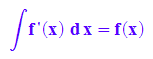
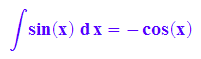
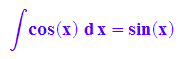
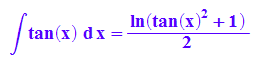
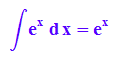
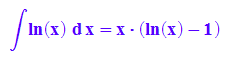
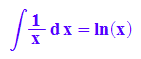
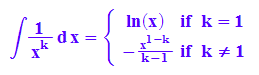
#############################################
Hauptsatz der Differential- und Integralrechung
hold(int(F'(x), x))=int(F'(x), x);
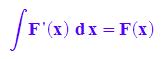
___________________________________
Bestimmte Intergale für einige Funktionen von a bis b
hold(int(1,x=a..b))=int(1, x=a..b);
hold(int(x,x=a..b))=int(x, x=a..b);
hold(int(x^2,x=a..b))=int(x^2, x=a..b);
hold(int(sin(x),x=a..b))=int(sin(x), x=a..b);
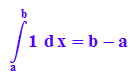
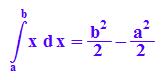
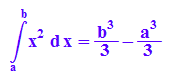
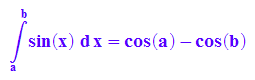
Teppich-Abroll-Funktion =Integralfunktion der oberen Grenze
hold(int(t^2,t=0..x))=int(t^2, t=0..x);
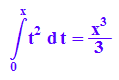
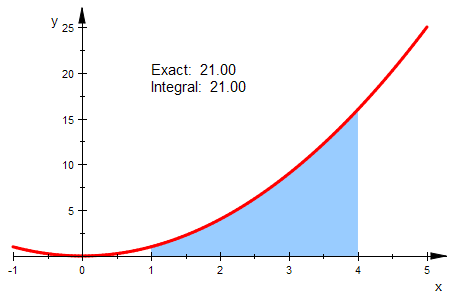
Beim Zeichnen Integral-Flächen muss man die Randfunktion als objekt erzeugen
parg:=plot::Function2d(x^2,x=-1..5,
LineColor=[1,0,0], LineWidth=0.8):
und die Fläche als plot::Integral von einem Funktions-Objekt mit den passenden Grenzen.
pari:=plot::Integral(plot::Function2d(x^2,x=1..4)):
plot(pari,parg)
Weiteres zum Integralezeichen und zu Riemannsummen in den anderen Dateien.
int(f'(x), x)
![]()