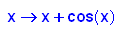Numerische Analysis Aufgabe
Prof. Dr. Dörte Haqftendorn, Jan 05
Stellen Sie f(x)=x+cos(x) aus Bausteinen dar. Berechen Sie die Nullstelle.
Berechnen sie das Volumen des Rotationskörpers (um die x-Achse)
zwischen der Nullstelle und PI genau und mit dem Keplerverfahren.

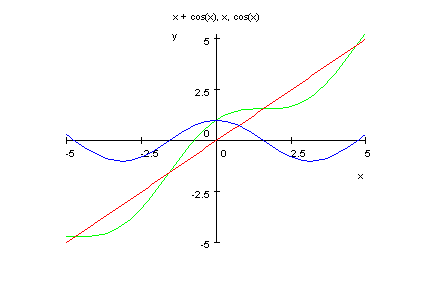
• plotfunc2d(x+cos(x),x,cos(x))

Die Nullstelle:

• loe:=op(numeric::solve(x+cos(x),x))

Das Rotationsvolumen

• PI*numeric::int((x+cos(x))^2,x=loe..PI)

• float(%)

• f:=x->(x+cos(x))

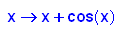
Mit Kepler-Regel:

• PI*(PI-loe)/6*(f(loe)^2+4*f((loe+PI)/2)^2+f(PI)^2)

• float(%)

Alternativ mit der Quadrierten Funktion und Kepler.

• g:=x->(x+cos(x))^2

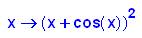
• PI*(PI-loe)/6*(g(loe)+4*g((loe+PI)/2)+g(PI))

• float(%)

Geometrische Vergleichskörper:
Zylinder und Kegel h=4, r=2

• h:=4:  r:=2:

• Vzyl:=PI*r^2*h; float(%)

• Vkeg:=Vzyl/3: float(%)

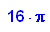
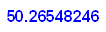
Passt dazwischen wie erwartet.