f:=x->a*x^2; f(x),f'(x),f''(x)
![]()
![]()
Evolute der Parabel
=Kurve der Mittelpunkte der Krümmungskreise
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4.0, Juni 06 Update 13.06.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
########################################################################
f:=x->a*x^2; f(x),f'(x),f''(x)
![]()
![]()
Krummung an der Stelle x
kappa:=x-->f''(x)/sqrt(1+f'(x)^2)^3
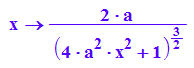
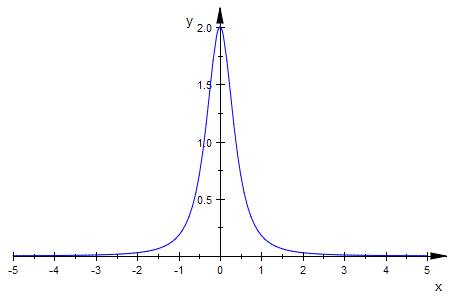
plotfunc2d(kappa(x)|a=1)
Radien der Krümmungkreise
r:=x-->1/kappa(x)
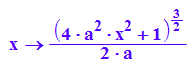
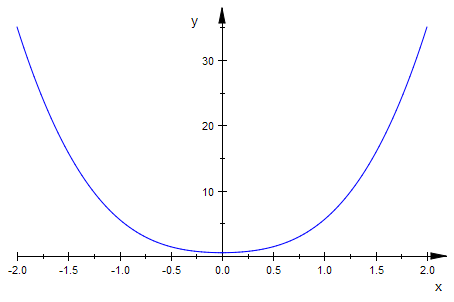
plotfunc2d(r(x)|a=1,x=-2..2)
Mittelpunkte der Krümmungskreise M=(m,n), Parameter t=x0
m:=t-->t-f'(t)/f''(t)*(1+f'(t)^2);
n:=t-->f(t)+1/f''(t)*(1+f'(t)^2)
![]()
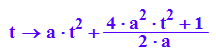
Das ist schon die Parameterdarstellung der Evolute= Kurve der M
evo:=plot::Curve2d([m(t),n(t)]|a=1,t=-2..2);plot(evo)
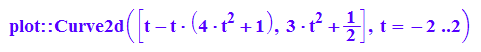
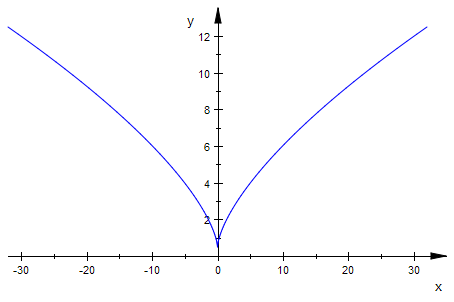
Dazu einzeichnen der Parabel und der halben Krümmungskreis mit M
a:=1:
par:=plot::Function2d(x^2,x=-5..5,
ViewingBoxYRange=0..10, LineColor=[1,0,0],LineWidth=0.8):
kkel:=plot::Arc2d(r(t),[m(t),n(t)],2..4,t=-2..0):
kker:=plot::Arc2d(r(t),[m(t),n(t)],-2..1,t=0..2, LineColor=[1,0,1]):
Ml:=plot::Point2d([m(t),n(t)],t=-2..0, PointSize=2):
Mr:=plot::Point2d([m(t),n(t)],t=0..2, PointSize=2, PointColor=[1,0,1]):
plot(par,evo,kkel,kker,Ml,Mr,ViewingBox=[-10..10,0..10]);
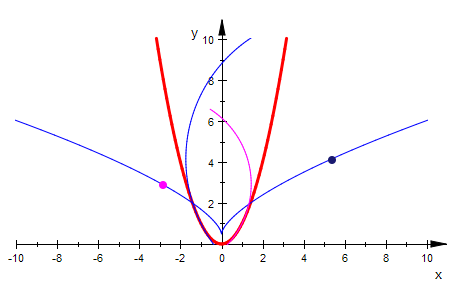
a:=1:
par:=plot::Function2d(x^2,x=-5..5,
ViewingBoxYRange=0..10, LineColor=[1,0,0],LineWidth=0.8):
kkelv:=plot::Arc2d(r(t/10),[m(t/10),n(t/10)],2..4)$ t=-20..0:
kkerv:=plot::Arc2d(r(t/10),[m(t/10),n(t/10)],-2..1, LineColor=[1,0,1])$ t=0..20:
Mlv:=plot::Point2d([m(t/10),n(t/10)], PointSize=2)$ t=-20..0:
Mrv:=plot::Point2d([m(t/10),n(t/10)], PointSize=2, PointColor=[1,0,1]) $ t=0..20:
plot(par,evo,kkelv,kkerv,Mlv,Mrv,par,ViewingBox=[-10..10,0..10]);
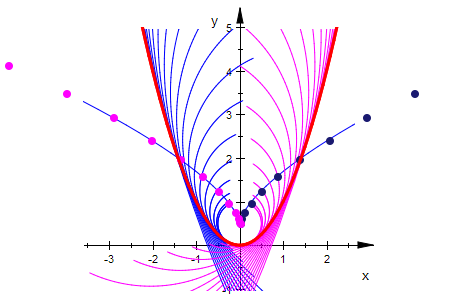

Die Krümmungskreise durchsetzen die Parabel am Berührpunkt.
Nur der SCheitelkeis in ganz im Innern der Parabel.
Zur Begründung wird die Krümmung als Funktion von x betrachtet:
Parabel und Krümmungsradius
plotfunc2d(r(x),f(x) ,x=-2..2)
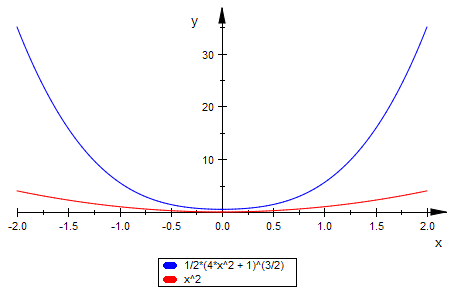
Parabel und Krümmung
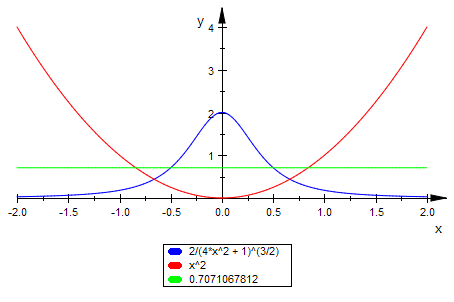
plotfunc2d(kappa(x),f(x), kappa(0.5),x=-2..2);
kappa(0.5);
![]()
Der Krümmungskreis des Scheitels liegt ganz in der Parabel. Alle anderen
Krümmungskreise durchsetzen die Parabel in Ihrem Berührpunkt. Denn z.B. ist
für die Berührstelle x=0.5 die Krümmung des Kreises konstant 0.707..., während sie
für die Parabel davor größer, danach kleiner ist, d.h. davor ist die Parabel innen,
danach ist sie außen.