Hüllparabel des rutschenden Geodreiecks
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4.0, ( MuPAD 3 im Apr. 06) Update 13.06.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
---------------------------------------------------------------------------------------------------------
Geradenschar, Hüllkurve aus der Extremalidee, Darstellung in 3D(x,t,z)
------------------------------------------------------------------------------------------------------
Lasse ein Geodreieck mit seiner rechten Ecke auf der x-Achse entlang
rutschen, so dass die eine Kathete den Punkt (0,a) (mit a=1) trifft.
Zeichne die andere Kathete als deutlichen Strich.
Tue das für viele Stellungen.

t =Stelle mit der rechten Ecke, F=(0,a)
Dann hat die Geradenschar folgende Gleichung:
g:=(x,t)->t/a*(x-t)
![]()
expand(g(x,t))
![]()
Die Schar der anderen Kante
a:=1:
k:=(x,t)->-a/t*(x-t):
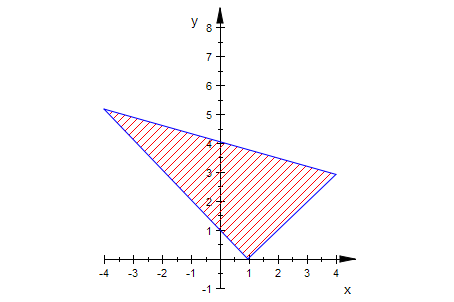
Darstellung des idealisierten Geo-Dreiecks
geo:=plot::Polygon2d([[-4,k(-4,t)],[t,0],[4,g(4,t)]],
t=0.5..3, Closed=TRUE, Filled=TRUE,
ViewingBox=[-4..4,-1..8], Scaling=Constrained,
AnimationStyle=BackAndForth):
plot(geo)

############################################
Schar der Geraden
alle:=plotfunc2d(g(x,t/10) $ t=-20..20,x=-4..4,LineWidth=0.6,
ViewingBoxYRange=-1..5,Scaling=Constrained,
LegendVisible=FALSE):
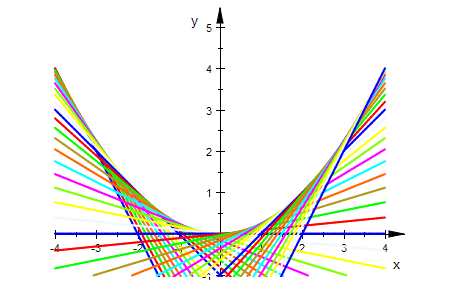
Hüllkurve aus Extremal-Idee.

Für jedes feste x muss die Gerade gefunden werden, die den größten Wert liefert.
Dafür muss man nach dem Paramter t partiell ableiten,
die Nullstellen der Ableitung (nach t aufgelöst) sind i.a. von x abhängige Terme.
Setzt man sie für t in g(x,t) ein, so erhält man ( hier) für jedes feste x den höchsten y-Wert, den es
über x gibt, das ist der y-Wert der Hüllkurven, also handelt es sich um die Gleichung der Hüllkurve.
Berechnung der Hüllkurve
delete(a):ab:=diff(g(x,t),t)
![]()
solve(ab=0,t)
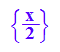
tg:=%[1]
![]()
g(x,tg)
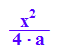
Diese Parabel ist die Hüllkurve des rutschenden Geodreiecks.
a:=1:alle2:=plot::Function2d(g(x,t/5),x=-4..4) $ t=-10..10:
para:=plot::Function2d(x^2/(4*a),x=-4..4,Color=RGB::Red, LineWidth=1):
plot(para,alle2,geo)
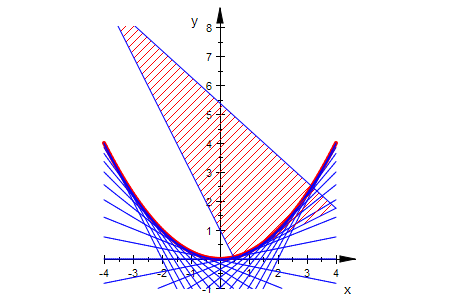

Parameterdarstellung der Hüllkurve
delete(a):
xe:=2*t:
ye:=g(xe,t)
![]()
a:=1:param:=plot::Curve2d([xe,ye],t=-2..2, LineWidth=1,LineColor=[1,0,0]):
plot(param,alle2, geo)
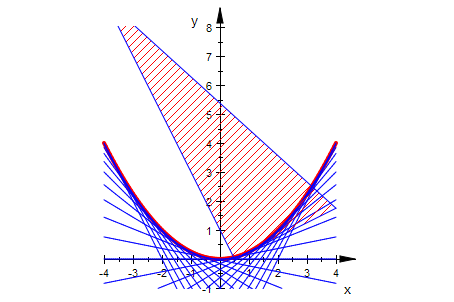

#################################################
Darstellung der Geraden im Raum
a:=1:
gerade:=plot::Curve3d([x,t, g(x,t)],x=-4..4,t=-2..2,
LineColor=[1,1,0], LineWidth=1,AnimationStyle=BackAndForth):
gr3d1:=plot::Function3d(g(x,t),x=-4..4,t=-2..2):
plot(gr3d1,gerade)
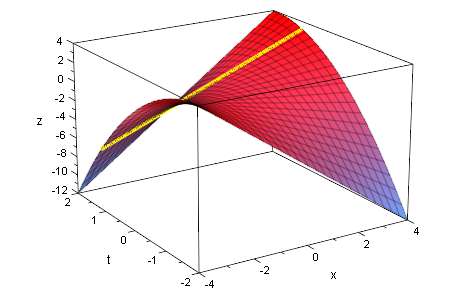

Kurve der Extrema im Raum=
Kurve im Raum, die die Berührpunkte verbindet
Diese kann man sich so vorstellen, dass man eine t-Achse als weitere Achse einfügt.
Dann ergibt sich die Kurve einfach aus [xe(t), t,ye(t)] als Parameterkurve.
beruehr:=[2*t,t,t^2/a]:
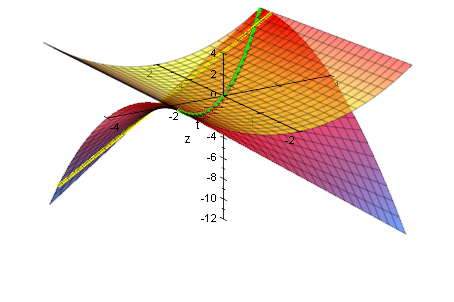
Hüllfläche und Berührkurve
Eine Hüllfäche könnte man wie eine Regenrinne konstruieren mit der Hüllkurve als Querschnitt.
Die Rinne ersteckt sich dann längs in Richtung der t-Achse.
Die Rinne kommt als 3D-Zeichnung zustande, wenn man einfach den Hüllkurventerm in den
3D-Zeichenbefehl schreibt. t ist dann beliebig.
gr3dHuelle:=plot::Function3d(x^2/(4*a),x=-4..4,t=-2..2, FillColorType=Rainbow, FillColor=[1,0,0,0.5]):
beruehrkurve:=plot::Curve3d([2*t,t,t^2/a],t=-2..2,LineWidth=1,Color=RGB::Green):
plot(gr3d1,gr3dHuelle,beruehrkurve,gerade, Axes=Origin)