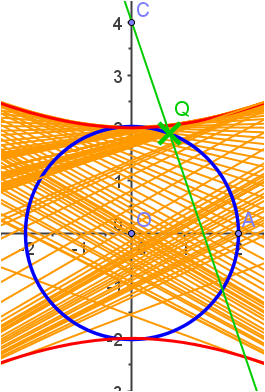
Hyperbel als Hüllkurve

Mathematik in wxMaxima www.mathematik-verstehen.de Haftendorn Dez 2010

Reidt-Wolf 4 S. 82

(%i2) load(draw)$

Konstruktionsbeschreibung:
A sei ein fester Punkt (R,0) auf der x-Achse.
C sei ein fester Punkt (0,c) auf der y-Achse.
Q wandert auf dem Kreis um O durch A.
Welche Hüllkurve hat die Normalenschar auf CQ in Q?

Figure 1:

(%i77) kill(R,u);

(%i78) v:sqrt(R^2-u^2);

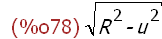
(%i79) g(x,u):=u/(c-v)*(x-u)+v;

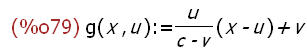
(%i80) diff(g(x,u),u,1);

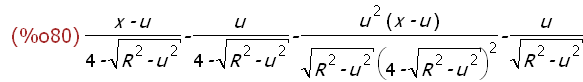
(%i81) xx:solve(diff(g(x,u),u,1)=0,x)[1];

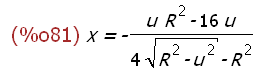
(%i82) fx(u):=rhs(xx);fx(u);

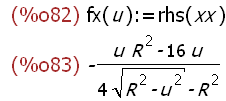
(%i84) g(fx(u),u);

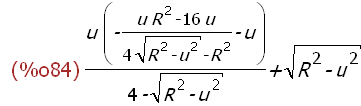
(%i85) fy(u):=facsum(g(fx(u),u));fy(u);

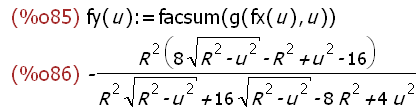
Parameterdarstellung

(%i44) fx(u); fy(u);

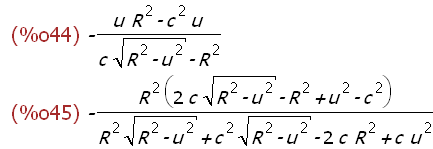
(%i88) load(draw)$

(%i89) R:2; c:4;

--> ku:gr2d(line_width=3,parametric(x,0,x,-4,6),color=green,points_joined=true,
points([[0,c],[1,sqrt(R^2-1)],
[1-c+sqrt(R^2-1), -1+sqrt(R^2-1)],[1+2*c-2*sqrt(R^2-1), 2+sqrt(R^2-1)]
]) , grid=true,
color=blue,parametric(R*cos(t),R*sin(t),t,0,2*%pi),
color=red,parametric(fx(u),-fy(u),u,-2,2),
parametric(fx(u),fy(u),u,-2,2),xrange=[-4,6],yrange=[-5,5])$

(%i159) draw(ku)$

Figure 2:

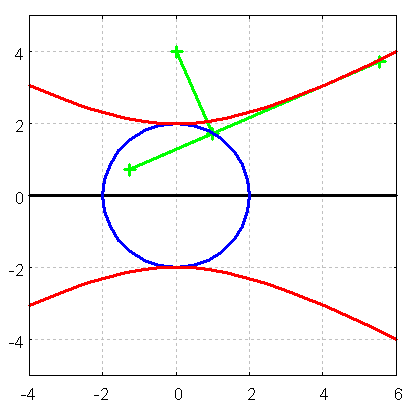
Versuch, die Hyperbel zu finden-

(%i160) fxx:eliminate([x=fx(u),y=fy(u)],[u]);

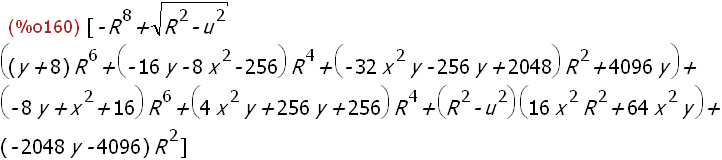
Hat nicht funktioniert, u ist noch drin.

Mathematica macht das problemlos.

(%i166) (fxx);

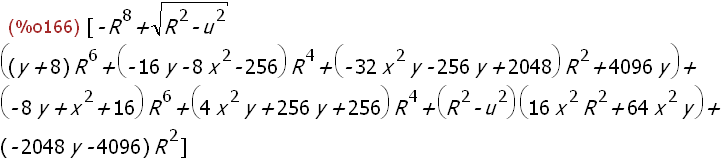
Der folgende Weg geht auch nicht, u bleibt auch drin

(%i167) xxu:solve(diff(g(x,u),u,1)=0,u)[1];

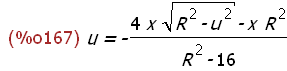
(%i168) ux:solve(xx,u);

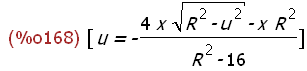
Achtung auch nicht ordentlich aufgelöst!!!