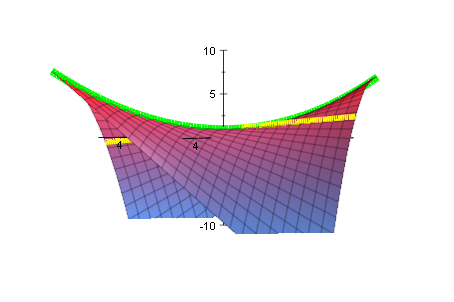
g:=(x,t)->t/p*(x-t/2)+p/2;g(x,t)
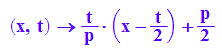
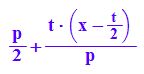
Knickparabel
Analysis 3D,Kurvenscharen mit Hüllkurve
Mathematik mit MuPAD 4, Prof. Dr. Dörte Haftendorn 02 Update Juni 07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
####################################################################
Handlung: Man markiert auf einem Blatt einen Punkt F zwei Finger breit von der langen Blattkante entfernt.
Nun knickt man so, dass die lange Blattkante den Punkt F trifft.
Das tut man oft. Die Knicke haben eine Hüllkurve.
Diese ist hier schon von Hand bestimmt, was sowohl geometrisch
als auch analytisch geht. und eine Parabel mit Brennpunkt F ergibt. Die lange Blattkante ist Leitgerade.
g:=(x,t)->t/p*(x-t/2)+p/2;g(x,t)
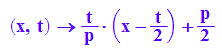
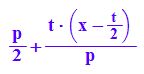
delete p:
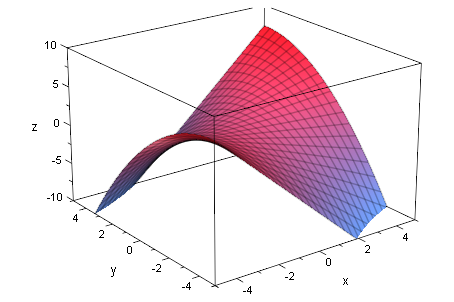
p:=2:
g3dp:=plot::Function3d(g(x,y),x=-5..5,y=-5..5,ViewingBoxZRange=-10..10):
plot(g3dp)
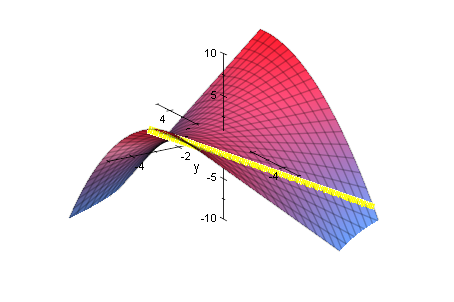
schar3dp:=plot::Curve3d([x,y,g(x,y)],x=-5..5,y=-3..3,
LineWidth=2,LineColor=[1,1,0], Axes=Origin):
plot(schar3dp,g3dp)

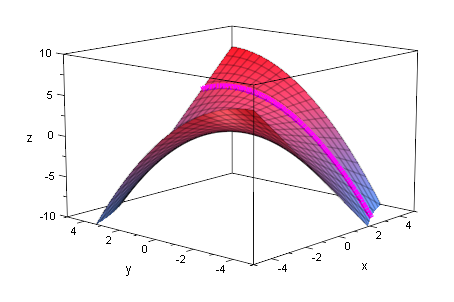
schnittezx:=plot::Curve3d([x,y,g(x,y)],y=-5..5,x=-3..3,
LineWidth=2,LineColor=[1,0,1]):
plot(g3dp, schnittezx)
diff(g(x,t),t)
![]()
g(t,t)
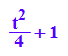
huell3dp:=plot::Curve3d([t,t,g(t,t)],t=-5..5,
LineWidth=2,LineColor=[0,1,0]):
plot(g3dp,huell3dp)
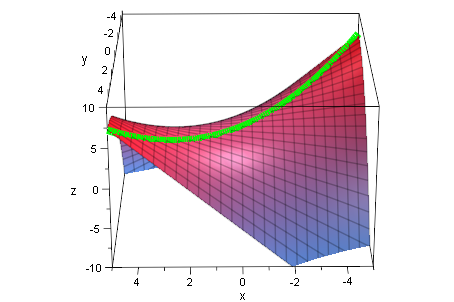
plot(g3dp,huell3dp,schar3dp)