g:=(x,t)->-1/(2*t)*x+1/2+t^2;
![]()
Normalenschar der Parabel 3D
und ihre Hüllkurve, die Evolute der Parabel in 3d-Darstellung
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4.0, Juni 06 Update 17.06.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
########################################################################
Berechnungen sind in der Datei Normalenschar-Parabel.mn
Die erzeugende Kurvenschar, hier die Normalenschar der Parabel, kann aufgefasst werden als eine
Raumfläche z=g(x,t). Die Hüllkurve besteht nur aus Punkten, die auch Punkte der Schar
sind. Also liegt die Hüllkurve auf dieser Raumfläche und jeder ihrer Punkte muss deren Gleichung erfüllen.
Außerdem muss sie in jedem ihrer Punkte eine waagerechte Tangente in t-Richtung haben.
Für benachbarte t müssen (in obigem Beispiel) nur höher gelegene Punkte der Raumfläche ergeben können.
Ausführliche Berechnung in der anderen Datei Normalenschar-Parabel. Man sollte aber
zuerst dieses 3d-Phänomen beim "rutschenden Geodreieck" betrachtet haben, dort ist die Raumfläche
einfacher zu überblicken.
Normalenschar:
g:=(x,t)->-1/(2*t)*x+1/2+t^2;
![]()
plotfunc3d(g(x,t), ViewingBox=[-4..4,-2..2,0..20])
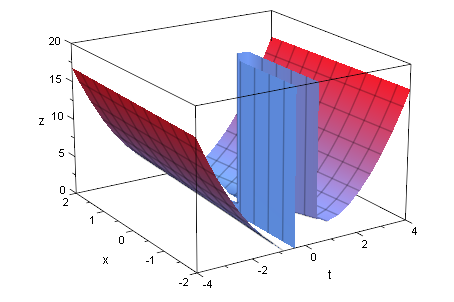
Die Hüllkurve ist in der anderen Datei berechnet zu
schar:=plot::Function3d(g(x,t), x=-4..4,t=-2..2,ViewingBox=[-4..4,-2..2,0..5]);
geraden:=plot::Curve3d([x,t,g(x,t)],x=-4..4,t=-2..2,
LineColor=[1,1,0], LineWidth=1,AnimationStyle=BackAndForth);
huell:=plot::Curve3d([-4*t^3,t,3*t^2+1/2],t=-2..2,
LineColor=[1,0,1], LineWidth=1);
huellfl1:=plot::Surface([-4*t^3,v,3*t^2+1/2],t=0..2,v=0.1..2,
FillColor=[0,1,0,0.5]);
huellfl2:=plot::Surface([-4*t^3,v,3*t^2+1/2],t=-2..0,v=-2..-0.1,
FillColor=[0,1,0,0.5]);
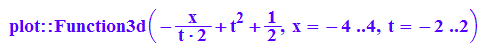
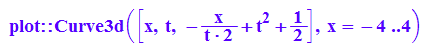
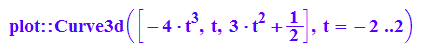
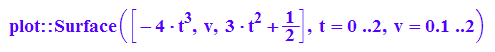
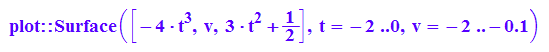
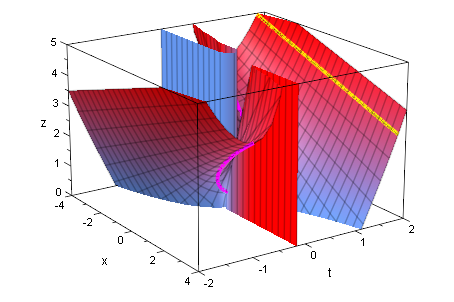
plot(schar,geraden,huell)

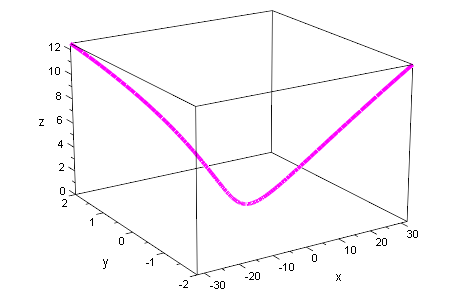
plot(huell)
Die Hüllkurvenfläche hat fast dieselbe Parameterdarstellung wie die Hüllkurve, man zieht
die Hüllkurve in t-Richtung einfach wie eine Rinne auseinander.
plot(geraden,huell,huellfl1, huellfl2,ViewingBox=[-8..8,-2..2,0..5])
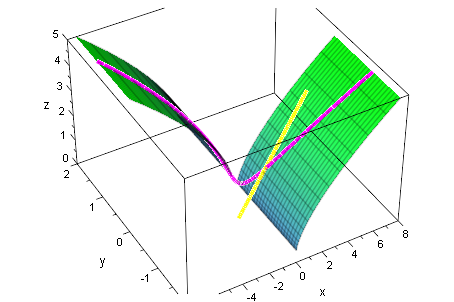

plot(schar,geraden,huell, huellfl1,huellfl2)
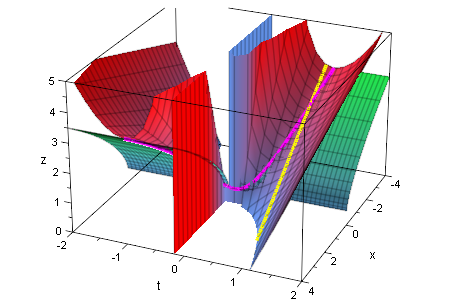

Die Hüllkurvenfläche schmiegt sich von unten an die Scharfläche an.
Die Berührkurve ist die Hüllkurve.
In jedem Punkt der Hüllkurve ist die Tangente in t-Richtung waagerecht,
die Ableitung also Null.
So wurde die Hüllkurve ja auch bestimmt in Version 1 und 3.