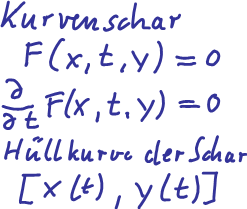f:=x->x^2;
![]()
Normalenschar und ihre Enveloppe
=Hüllkurve. Es ist die Evolute der Parabel
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 4.0, Juni 06 Update 17.06.07
https://mathe.web.leuphana.de www.mathematik-verstehen.de
########################################################################
Bestimmung der Hüllkurve= Eveloppe der Normalenschar der Normalparabel
f:=x->x^2;
![]()
Normalenschar, Parameter t=x0
g:=x-->expand(-1/f'(t)*(x-t)+f(t));
![]()
Version 1, Bestimmung aus der Extremal-Idee:
An der Stelle x hat diejenige Normale
mit der Hüllkurve einen Punkt gemeinsam, die an der Stelle x den höchsten
(oder kleinsten) Wert hat.
gpunkt:=diff(g(x),t)
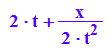
xh:=solve(gpunkt=0,x)[1]
![]()
yh:=expand(g(xh))
![]()
Dieses ist die Parameterdarstellung der Hüllkurve
huell:=plot::Curve2d([xh,yh],t=-2..2)
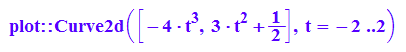
plot(huell)
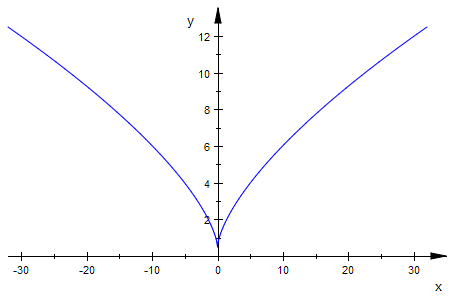
Hüllkurve oder Enveloppe
huell:=plot::Curve2d([xh,yh],t=-4..4):
par:=plot::Function2d(x^2,x=-5..5,
ViewingBoxYRange=0..10, LineColor=[1,0,0],LineWidth=0.8):
ge:=(plot::Function2d(g(x)|t=k/10,x=-5..0)$ k=1..15):
gel:=(plot::Function2d(g(x)|t=k/10,x=-0..5)$ k=-15..-1):
geani:=(plot::Function2d(g(x)|t=k/10,x=-5..5, k=1..15, LineColor=[1,1,0],LineWidth=0.8)):
gelani:=(plot::Function2d(g(x)|t=k/10,x=-5..5,k=-15..-1, LineColor=[1,0,1],LineWidth=0.8)):
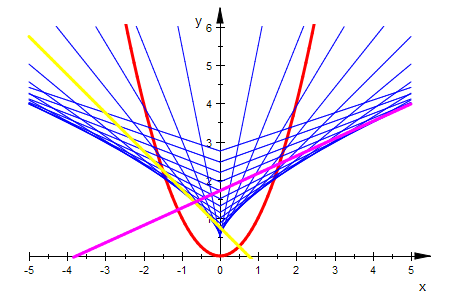
Parabel, Normalenschar und zwei bewegliche Normalen:
plot(huell,par,ge,gel,geani,gelani,ViewingBox=[-5..5,0..6], Scaling=Constrained)

Mittelpunkte der Krümmungkeise, siehe Datei: Evolute der Parabel
m:=x->4*t^3;
n:=x->1/2+3*t^2;
![]()
![]()
Das ist die Parameterdarstellung der Evolute. Einzeichnung
evo:=plot::Curve2d([m(t),n(t)],t=-2..2,LineStyle=Dashed, LineColor=[0,0,0], LineWidth=1.5):
plot(huell,par,ge,gel,geani,gelani,evo, ViewingBox=[-5..5,0..6], Scaling=Constrained)
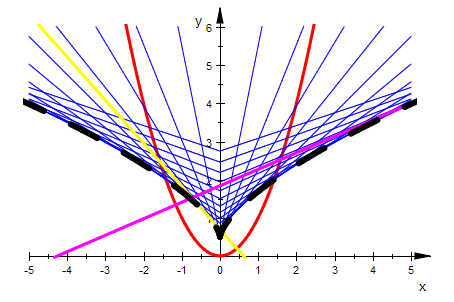

Man sieht, dass die Hüllkurve (Enveloppe) der Nomalenschar übereinstimmt mit der
Evolute der Parabel, der Kurve ihrer Krümmungskreismittelpunkte.
Version 2 Bestimmung der Hüllkurve aus der Schnittidee:
Es werden die Normalen zu t und zu k zum Schnitt gebracht. Dann lässt man
k gegen t streben und der Mittelpunkt des Krümmungskreises muss sich ergeben.
gk:=g(x)|t=k
![]()
xs:=solve (g(x)=gk,x)[1][1]
![]()
limit(xs,k=t)
![]()
Das ist xh, wie oben, weiter wie oben.
#########################################
Version 3 Bestimmung der Hüllkurve aus Idee der Schar als
Raumfläche:
Die erzeugende Kurvenschar, hier die Normalenschar, kann aufgefasst werden als eine
Raumfläche z=g(x,t). Die Hüllkurve besteht nur aus Punkten, die auch Punkte der Schar
sind. Also liegt die Hüllkurve auf dieser Raumfläche und jeder ihrer Punkte muss deren Gleichung erfüllen.
Außerdem muss sie in jedem ihrer Punkte eine waagerechte Tangente in t-Richtung haben.
Für benachbarte t müssen (in obigem Beispiel) nur höher gelegene Punkte der Raumfläche ergeben können.
Ausführliche 3d-Darstellung in der anderen Datei Normalenschar-Parabel-3d. Man sollte aber
zuerst diese Phänomen beim "rutschenden Geodreieck" betrachtet haben, dort ist die Raumfläche
einfacher zu überblicken.
Da eine Parameterdarstellung der Hüllkurve gesucht ist, also x=xh(t), y=yh(t), müssen diese
Koordinaten ebenso wie deren partielle Ableitungen die Normalengleichung und deren
Ableitung erfüllen.

Allgemein kann man die Kurvenschar, die die Hüllkurve erzeugt, schreiben als
F(x,t,y)=0 . Die Hüllkurve [x(t), y(t)] muss diese Gleichung erfüllen und deren
partielle Ableitung nach t.